深度学习之图像分类（二十五）-- S2MLPv2网络详解-木卯 Blog

深度学习之图像分类（二十五）S2MLPv2网络详解

经过 S2MLP 和 Vision Permutator 的沉淀，为此本节我们便来学习学习 S2MLPv2 的基本思想。

1. 前言

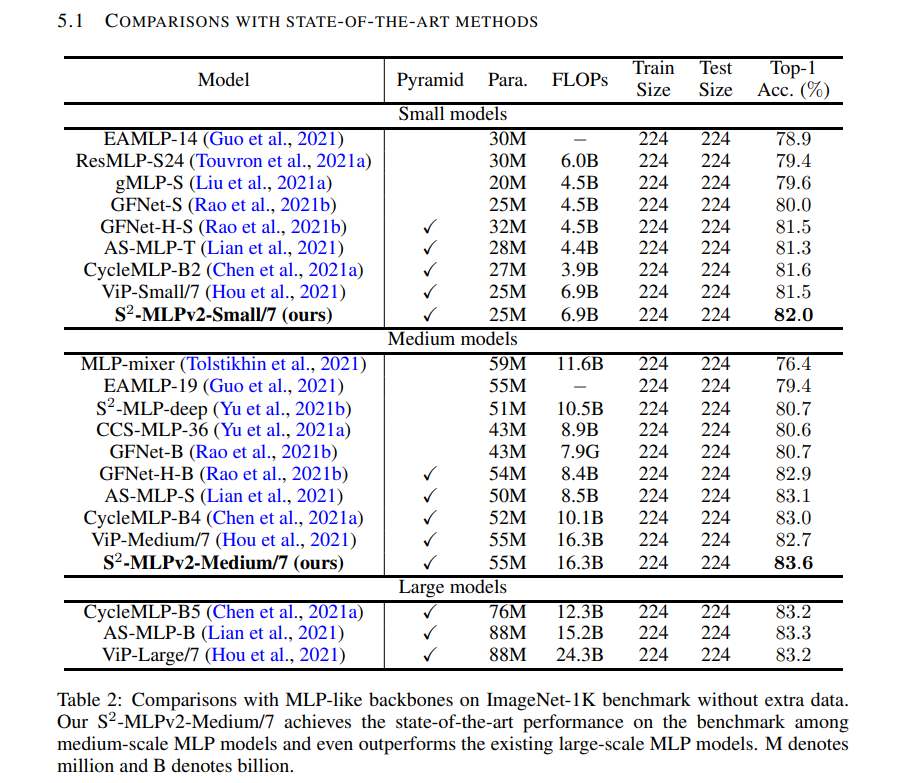
S2MLPv2 依是百度提出的用于视觉的空间位移 MLP 架构，其作者以及顺序与 S2MLP 一模一样，其论文为 S2-MLPv2: Improved Spatial-Shift MLP Architecture for Vision。S2MLPv2 的修改点主要在于三处：金字塔结构（参考 ViP）、分三类情况进行考虑（参考 ViP）、使用 Split Attention（参考 ViP 和 ResNeSt）。总结而言就是把 ViP 中的 Permute-MLP layer 中别人沿着不同方向进行交互替换为了 Spatial-shift 操作。在参数量基本一致的情况下，其性能优于 ViP。

2. S2MLPv2

2.1 S2MLPv2 Block

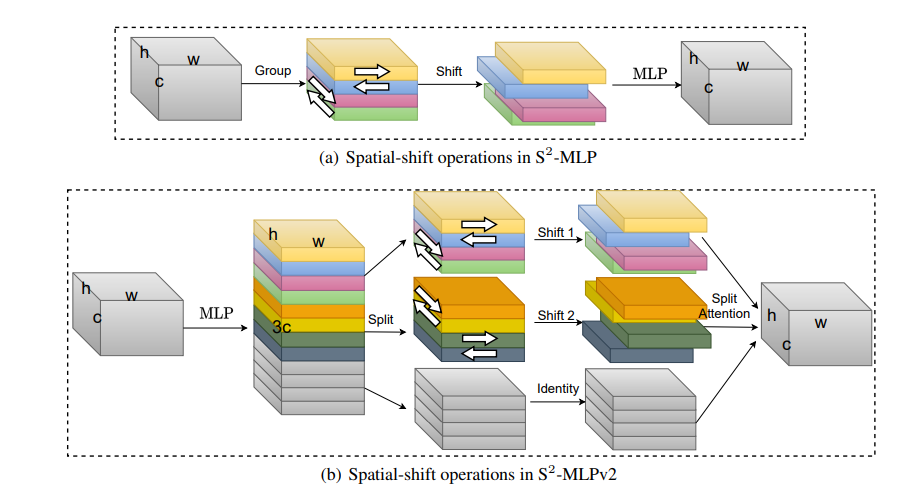
S2MLPv2 和 S2MLPv1 类似，整体网络结构不做过多赘述，主要讲解一下 S2MLPv2 Block 的细节（建议大家先回顾之前的章节 S2MLP 以及 ViP）：

首先是特征图输入后，对 Channel 进行一个全连接，这里是对于特定位置信息进行交流，其实也就是 $1 \times 1$ 卷积，只不过这里将维度变为了原来的 3 倍。然后经过一个 GELU 激活函数。
将特征图均分为 3 等分，分别用于后续三个 Spatial-shift 分支的输入。
- 第一个分支进行与 S2MLPv1 一样的 Spatial-shift 操作，即右-左-下-上移动。
- 第二个分支进行与第一个分支反对称的 Spatial-shift 操作，即下-上-右-左移动。
- 第三个分支保持不变
之后将三个分支的结果通过 Split Attention 结合起来。这样不同位置的信息就被加到同一个通道上对齐了。
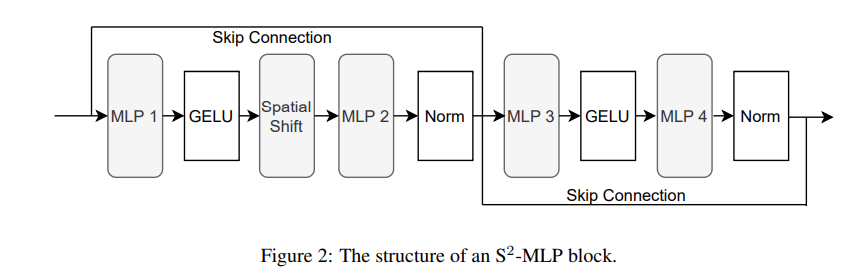
再经过一个 MLP 进行不同位置的信息整合，然后经过 LN 激活函数。（看了这么多网络，其实激活函数在前在后都可以）

def spatial_shift1(x):
    b,w,h,c = x.size()
    x[:,1:,:,:c/4] = x[:,:w-1,:,:c/4]
    x[:,:w-1,:,c/4:c/2] = x[:,1:,:,c/4:c/2]
    x[:,:,1:,c/2:c*3/4] = x[:,:,:h-1,c/2:c*3/4]
    x[:,:,:h-1,3*c/4:] = x[:,:,1:,3*c/4:]
    return x

def spatial_shift2(x):
    b,w,h,c = x.size()
    x[:,:,1:,:c/4] = x[:,:,:h-1,:c/4]
    x[:,:,:h-1,c/4:c/2] = x[:,:,1:,c/4:c/2]
    x[:,1:,:,c/2:c*3/4] = x[:,:w-1,:,c/2:c*3/4]
    x[:,:w-1,:,3*c/4:] = x[:,1:,:,3*c/4:]
    return x

class S2-MLPv2(nn.Module):
    def __init__(self, channels):
        super().__init__()
        self.mlp1 = nn.Linear(channels,channels * 3)
        self.mlp2 = nn.Linear(channels,channels)
        self.split_attention = SplitAttention()
    def forward(self, x):
        b,w,h,c = x.size()
        x = self.mlp1(x)
        x1 = spatial_shift1(x[:,:,:,:c/3])
        x2 = spatial_shift2(x[:,:,:,c/3:c/3*2])
        x3 = x[:,:,:,c/3*2:]
        a = self.split_attention(x1,x2,x3)
        x = self.mlp2(a)
        return x

接下来的就是和 MLP-Mixer 中的 Channel-mixing MLP 一致。

2.2 Spatial-shift 与感受野反思

三组 Spatial-shift （包括恒等）与一组相比有什么进步和问题呢？

传统计算机视觉感受野以及近期 ViP 工作等等，都提倡奇数和中心概念，即在某中心卷积核大小是奇数的，一左一右一上一下是对称的。原始的一组 Spatial-shift 其实是一个菱形感受野且不包括中心。现在有恒等之后则是菱形感受野且包括中心了，这是一个进步。
但是第二组设计为与第一组反对称的结构，但是这个反没有反彻底。其实这三组 Spatial-shift 也可看作是人精心设计构造的。那么我们仔细看一下，其实没有实现完全的互补。让我们把目光放到 Split Attention 之后，输出的特征图其实也可被看作四个部分，每部分对应着：左上中相加，右下中相加，上左中相加，下右中相加。为了更好的方便大家理解这句话，我们不妨先忽略 Split Attention 给出的权重，并将经过 Spatial-shift 操作前的三部分特征图分别记录为 $f,g,h$，输出记录为 $z$。则有如下公式，其中下标表示不同的旋转部分。
- 如果从强迫症的观点看：第一组 Spatial-shift 是右-左-下-上，则第二组 Spatial-shift 应该是上-下-右-左才对。
- 如果从感受野完整性的观点看：第一组 Spatial-shift 是右-左-下-上，则第二组 Spatial-shift 应该是左上-左下-右上-右下才对。

\[z_{1}(x,y) = f_{1}(x-1,y) + g_{1}(x,y-1) + h_{1}(x,y) \\ z_{2}(x,y) = f_{2}(x+1,y) + g_{2}(x,y+1) + h_{2}(x,y) \\ z_{3}(x,y) = f_{3}(x,y-1) + g_{3}(x-1,y) + h_{3}(x,y) \\ z_{4}(x,y) = f_{4}(x,y+1) + g_{4}(x+1,y) + h_{4}(x,y)\]

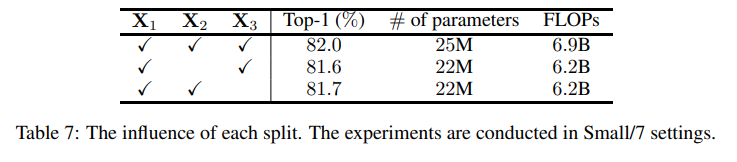
关于 Split 的消融实验，作者分别移除了第二部分和第三部分，发现移除第二部分损失的性能还比第三部分（恒等）的多，但是就差 0.1\%，这个消融实验其实很难解释三部分怎么相互作用的，至少从计算机视觉感受野的角度不太说得清楚。或许 MLP 结构就不太适合用感受野来分析吧…

3. 总结

相比于现有的 MLP 的结构，S2-MLP 的一个重要优势是仅仅使用通道方向的全连接（$1 \times 1$ 卷积）是可以作为 Backbone 的，期待该团队后续的进展。S2-MLPv2 其实是通过 Spatial-shift 和 Split Attention 代替原有的 $N \times N$ 卷积，本质上并没有延续 MLP-Mixer 架构中长距离依赖的思想。S2-MLPv2 中也并没有长距离依赖的使用。S2-MLPv2 虽然性能提升了，但是还没有开源，本身自己的贡献点其实不太足，这样做的理论性也不足。

延续我一贯的认识，如何在 MLP 架构中如何结合图像局部性和长距离依赖依然是值得探讨的点。

### 4. 代码

代码并没有开源，非官发复现的代码详见此处。

import torch
from torch import nn
from einops.layers.torch import Reduce
from .utils import pair

class PreNormResidual(nn.Module):
    def __init__(self, dim, fn):
        super().__init__()
        self.fn = fn
        self.norm = nn.LayerNorm(dim)

    def forward(self, x):
        return self.fn(self.norm(x)) + x

def spatial_shift1(x):
    b,w,h,c = x.size()
    x[:,1:,:,:c//4] = x[:,:w-1,:,:c//4]
    x[:,:w-1,:,c//4:c//2] = x[:,1:,:,c//4:c//2]
    x[:,:,1:,c//2:c*3//4] = x[:,:,:h-1,c//2:c*3//4]
    x[:,:,:h-1,3*c//4:] = x[:,:,1:,3*c//4:]
    return x

def spatial_shift2(x):
    b,w,h,c = x.size()
    x[:,:,1:,:c//4] = x[:,:,:h-1,:c//4]
    x[:,:,:h-1,c//4:c//2] = x[:,:,1:,c//4:c//2]
    x[:,1:,:,c//2:c*3//4] = x[:,:w-1,:,c//2:c*3//4]
    x[:,:w-1,:,3*c//4:] = x[:,1:,:,3*c//4:]
    return x

class SplitAttention(nn.Module):
    def __init__(self, channel = 512, k = 3):
        super().__init__()
        self.channel = channel
        self.k = k
        self.mlp1 = nn.Linear(channel, channel, bias = False)
        self.gelu = nn.GELU()
        self.mlp2 = nn.Linear(channel, channel * k, bias = False)
        self.softmax = nn.Softmax(1)
    
    def forward(self,x_all):
        b, k, h, w, c = x_all.shape
        x_all = x_all.reshape(b, k, -1, c)          #bs,k,n,c
        a = torch.sum(torch.sum(x_all, 1), 1)       #bs,c
        hat_a = self.mlp2(self.gelu(self.mlp1(a)))  #bs,kc
        hat_a = hat_a.reshape(b, self.k, c)         #bs,k,c
        bar_a = self.softmax(hat_a)                 #bs,k,c
        attention = bar_a.unsqueeze(-2)             # #bs,k,1,c
        out = attention * x_all                     # #bs,k,n,c
        out = torch.sum(out, 1).reshape(b, h, w, c)
        return out

class S2Attention(nn.Module):
    def __init__(self, channels=512):
        super().__init__()
        self.mlp1 = nn.Linear(channels, channels * 3)
        self.mlp2 = nn.Linear(channels, channels)
        self.split_attention = SplitAttention(channels)

    def forward(self, x):
        b, h, w, c = x.size()
        x = self.mlp1(x)
        x1 = spatial_shift1(x[:,:,:,:c])
        x2 = spatial_shift2(x[:,:,:,c:c*2])
        x3 = x[:,:,:,c*2:]
        x_all = torch.stack([x1, x2, x3], 1)
        a = self.split_attention(x_all)
        x = self.mlp2(a)
        return x

class S2Block(nn.Module):
    def __init__(self, d_model, depth, expansion_factor = 4, dropout = 0.):
        super().__init__()

        self.model = nn.Sequential(
            *[nn.Sequential(
                PreNormResidual(d_model, S2Attention(d_model)),
                PreNormResidual(d_model, nn.Sequential(
                    nn.Linear(d_model, d_model * expansion_factor),
                    nn.GELU(),
                    nn.Dropout(dropout),
                    nn.Linear(d_model * expansion_factor, d_model),
                    nn.Dropout(dropout)
                ))
            ) for _ in range(depth)]
        )

    def forward(self, x):
        x = x.permute(0, 2, 3, 1)
        x = self.model(x)
        x = x.permute(0, 3, 1, 2)
        return x

class S2MLPv2(nn.Module):
    def __init__(
        self,
        image_size=224,
        patch_size=[7, 2],
        in_channels=3,
        num_classes=1000,
        d_model=[192, 384],
        depth=[4, 14],
        expansion_factor = [3, 3],
    ):
        image_size = pair(image_size)
        oldps = [1, 1]
        for ps in patch_size:
            ps = pair(ps)
            assert (image_size[0] % (ps[0] * oldps[0])) == 0, 'image must be divisible by patch size'
            assert (image_size[1] % (ps[1] * oldps[1])) == 0, 'image must be divisible by patch size'
            oldps[0] = oldps[0] * ps[0]
            oldps[1] = oldps[1] * ps[1]
        assert (len(patch_size) == len(depth) == len(d_model) == len(expansion_factor)), 'patch_size/depth/d_model/expansion_factor must be a list'
        super().__init__()

        self.stage = len(patch_size)
        self.stages = nn.Sequential(
            *[nn.Sequential(
                nn.Conv2d(in_channels if i == 0 else d_model[i - 1], d_model[i], kernel_size=patch_size[i], stride=patch_size[i]),
                S2Block(d_model[i], depth[i], expansion_factor[i], dropout = 0.)
            ) for i in range(self.stage)]
        )

        self.mlp_head = nn.Sequential(
            Reduce('b c h w -> b c', 'mean'),
            nn.Linear(d_model[-1], num_classes)
        )

    def forward(self, x):
        embedding = self.stages(x)
        out = self.mlp_head(embedding)
        return out