深度学习之图像分类（二十四）-- Vision Permutator网络详解-木卯 Blog

深度学习之图像分类（二十四）Vision Permutator网络详解

为了承接前文 S2MLP 以及之后的 S2MLPv2，本章节学习 Vision Permutator 网络。

1. 前言

ViP (Vision Permutator) 是新加坡国立南开等机构联合提出的新型 MLP 架构，论文为 VISION PERMUTATOR: A PERMUTABLE MLP-LIKE ARCHITECTURE FOR VISUAL RECOGNITION。MLP-Mixer 的 token-mixing MLP 是全局感受野，AS-MLP 我们分析了其实是一个近似 $3 \times 3$ 到 $5 \times 5$ 的局部感受野，S2MLP 也是一个上下左右的菱形感受野。那么在他们中间还有没有什么形式的感受野呢？答案是有的：那就是沿着特定方向一条线的感受野。如果我们将全局感受野看作一个面，局部感受野看成一个点，那么在他们之间的就是一条线。所以与最近的类似 MLP 的模型沿展平的空间维度对空间信息进行编码不同，Vision Permutator 使用线性投影分别沿高度和宽度维度对特征表示进行编码。这允许 Vision Permutator 沿一个空间方向捕获长距离依赖关系，同时沿另一个方向保留精确的位置信息。然后以相互补充的方式聚合得到的位置敏感输出，以形成感兴趣对象的表达表示。

2. ViP 网络结构

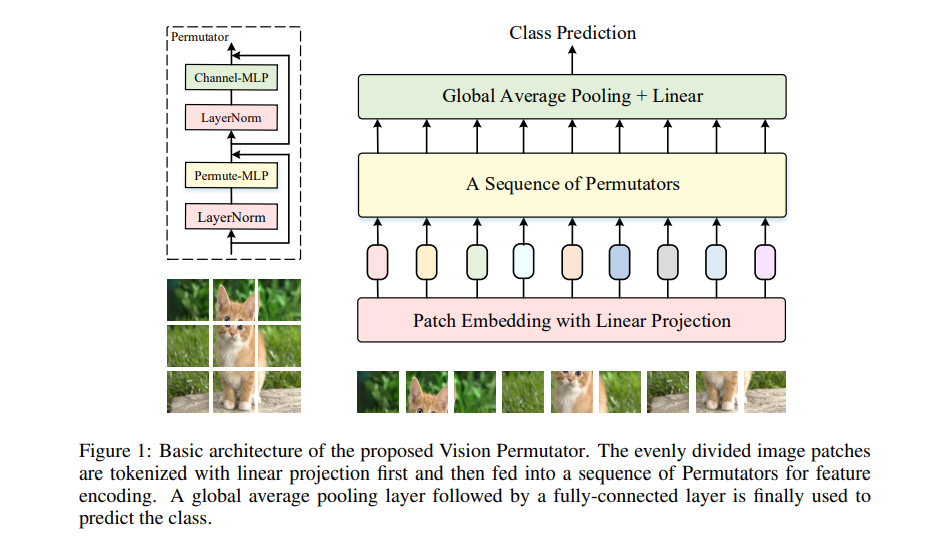
ViP 和 S2MLP 类似，整体网络结构如下图所示，其中 Permutators 模块被重复了多次。我们先来全局性地讲一下 ViP 怎么工作的：

首先是对于一个 $3 \times H \times W$ 的输入 RGB 图像，将其进行 patch 切片，patch 大小为 $p \times p$，patch 的个数为 $\frac{H}{p} \times \frac{W}{p}$，并将 patch 展平为一个向量，维度为 $3p^2$。然后经过一个 patch-wise fully-connected layer (其实也就是 $1 \times 1$ 卷积)，将 $3p^2$ 降维为 $c$。在全连接层后有一个 LN 层进行归一化。令 $h = \frac{H}{p}, w = \frac{W}{p}$，此时我们就有 $h \times w \times c$ 的一个矩阵。作者使用过程中 $c = 384$， $p = 14$ ，此时 $h \times w = 256$。
随后 $h \times w \times c$ 的特征图被视为 $h \times w$ 个 token，每个 token 的维度为 $c$。之后经过 N 个 Permutators，其中每个 Block 包含了一个 Permute-MLP 和一个 Channel-mixing MLP，两个残差结构，这些基本配置和 MLP-Mixer 是一致的，唯一的不同就是把 token-mixing MLP 替换为了Permutators。值得注意的是，Channel-mixing MLP 第一个全连接层通常会对节点数进行扩充，再通过 Channel-mixing MLP 第二个全连接层还原回来。这里第一个全连接层的 MLP Ratio 被设置为 3（ViT 等工作的设置为 4）。
最后的输出结果经过全局平均池化和全连接层，就可以得到输出了。

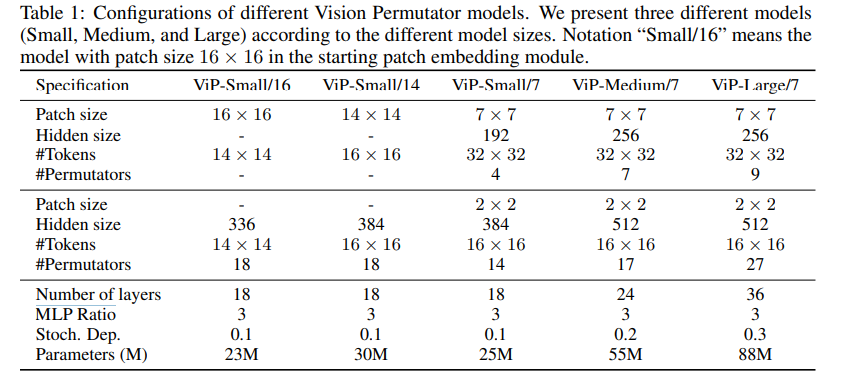
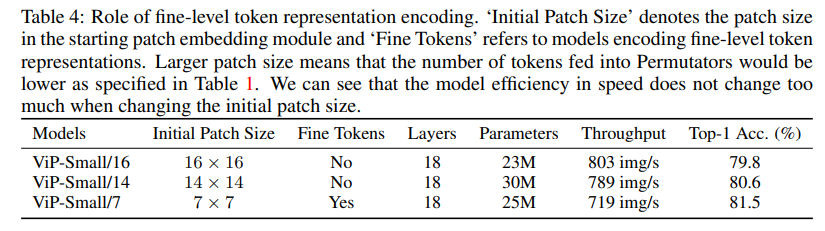
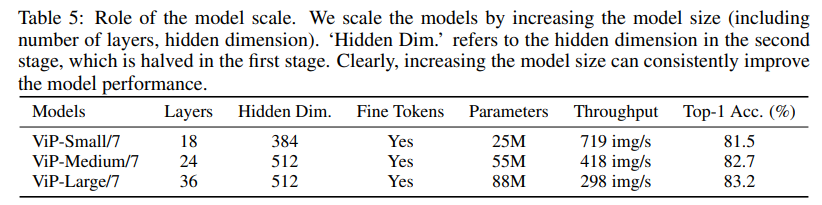
不同配置的 ViP 网络的配置表如下， ViP-Small/16 表示初始 patch 大小为 $16 \times 16$。注意到 ViP 也创新性地给出了两阶段的 ViP，即中间进行了一次 $2 \times 2$ 共计 4 个 patch 的合并下采样（通道数变为 4 倍，即 256 * 4 = 1024），并经过 $1 \times 1$ 卷积将通道变为 1/2，即 512。这种分 stage 的操作其实已经有构建 backbone 的意思了，但是可惜作者并没有继续下去。实验也表明，patch 越小，信息越密，增加的细粒度编码有助于模型性能的提升，性能越好；分两阶段的比一阶段的还要好。This indicates that we can appropriately use smaller initial patch size to improve the model performance.

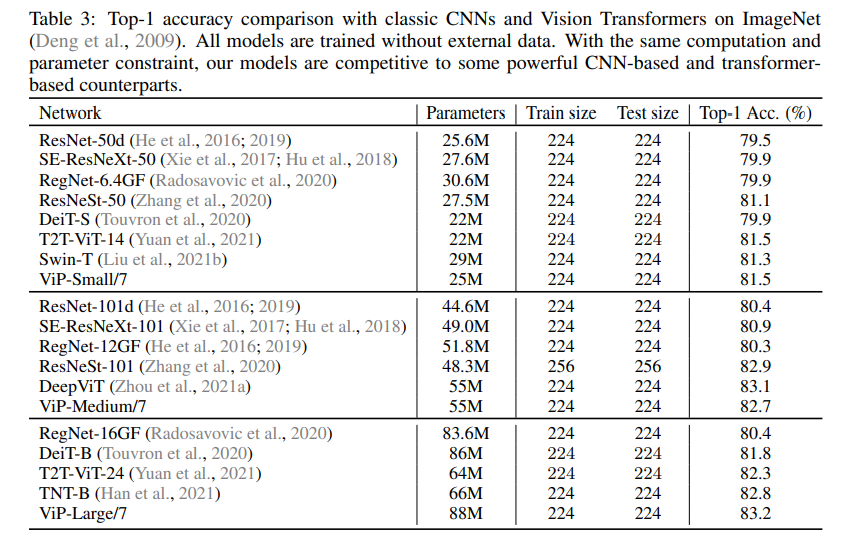
此外， token 数量越大，隐含层越多，ViP 还能继续提升性能。整个实验在 ImageNet-1k 上进行训练和测试，其中小规模模型的训练使用了 8xV100 显卡，而大规模模型需要两个 8 卡节点进行训练。实验中还利用了 CutOut，CutMix，MixUp，RandAug 等增强方式扩充了数据，最终测试使用了单个 V100-32G 进行。

3. Permutators

3.1 Permute-MLP 结构

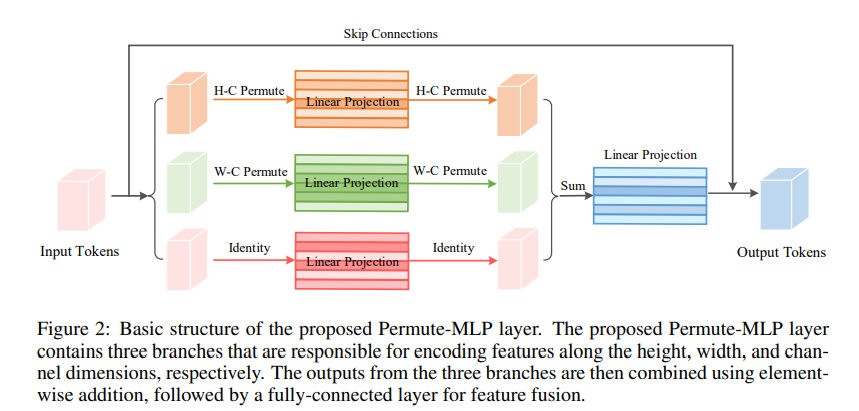
在对 ViP 网络整体有个概念后，我们来看看单个 Permutators 是怎么设计的。ViP 网络中最为重要的是 Permutator 模块中的 Permute-MLP 层，这是本文的关键创新所在。假设经过 token 处理的特征图具有 H-W-C 大小，Permutator 将这一三维的 token 表达分别送入三个分支中，其中在通道方向上采用正常的线性全连接层进行处理，而在宽度和高度方向则对特征进行了重新排量与整合，从而进行逐个方向的独立编码，Permutator 的称号也由此而来。Permute-MLP 层最大的特点在于其中包含了为宽度方向、长度方向和通道方向独立建模的三个分支，具体结构如下图所示。

伪代码实现如下所示：

# Algorithm 1 Code for Permute-MLP (PyTorch-like)
# H: height, W: width, C: channel, S: number of segments
# x: input tensor of shape (H, W, C)

################### initialization ####################################################
proj_h = nn.Linear(C, C) # Encoding spatial information along the height dimension
proj_w = nn.Linear(C, C) # Encoding spatial information along the width dimension
proj_c = nn.Linear(C, C) # Encoding channel information
proj   = nn.Linear(C, C) # For information fusion

#################### code in forward ##################################################
def permute_mlp(x):
    N = C // S
    x_h = x.reshape(H, W, N, S).permute(2, 1, 0, 3).reshape(N, W, H*S)
    x_h = self.proj_h(x_h).reshape(N, W, H, S).permute(2, 1, 0, 3).reshape(H, W, C)
    x_w = x.reshape(H, W, N, S).permute(0, 2, 1, 3).reshape(H, N, W*S)
    x_w = self.proj_w(x_w).reshape(H, N, W, S).permute(0, 2, 1, 3).reshape(H, W, C)
    x_c = self.proj_c(x)
    x = x_h + x_w + x_c
    x = self.proj(x)
    return x

如果要对 H 方向进行映射，那么首先就是进行特征矩阵的转置，即 (H,W,C) –> (C,W,H)。但是实际上作者分成了 S 段来实现。可能会觉得奇怪，proj_c 是 nn.Linear(C, C) 可以理解，但是 proj_h 和 proj_w 为什么是 nn.Linear(C, C)？

答：首先注意到输入图片是方的 ($224 \times 224$)，patch 也是方的 (例如 $14 \times 14$)，所以输入 Permutator 的特征矩阵也是方的，即 $H = W$。作者在实际实现中，C 是 H 和 W 的倍数，所以直接取 $N = H$ 或者 $N = W$，从而使得 $H \times S = W \times S = N \times S = C$。

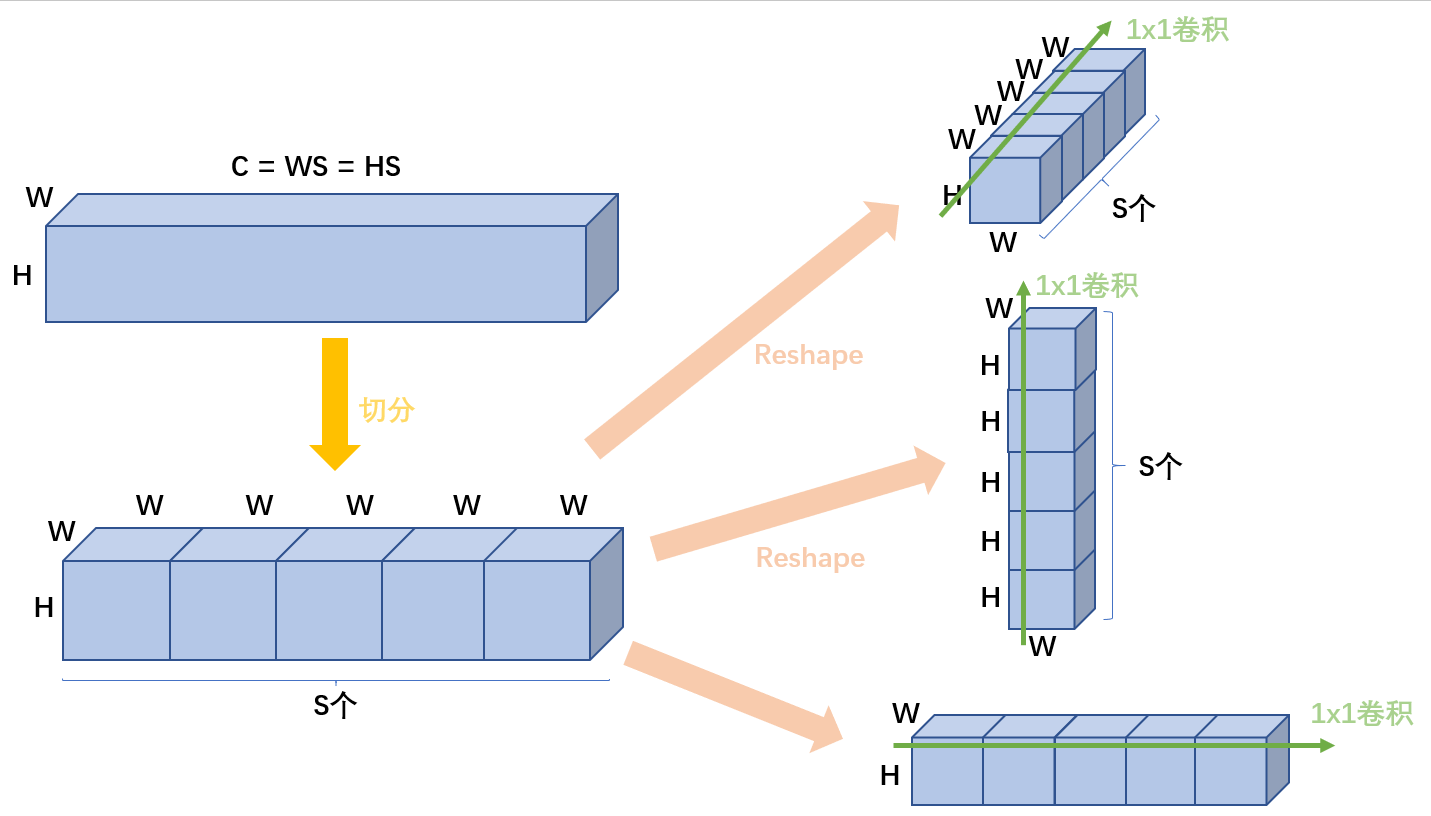
其次，如何理解这里的分 S 段，即 N = C // S？

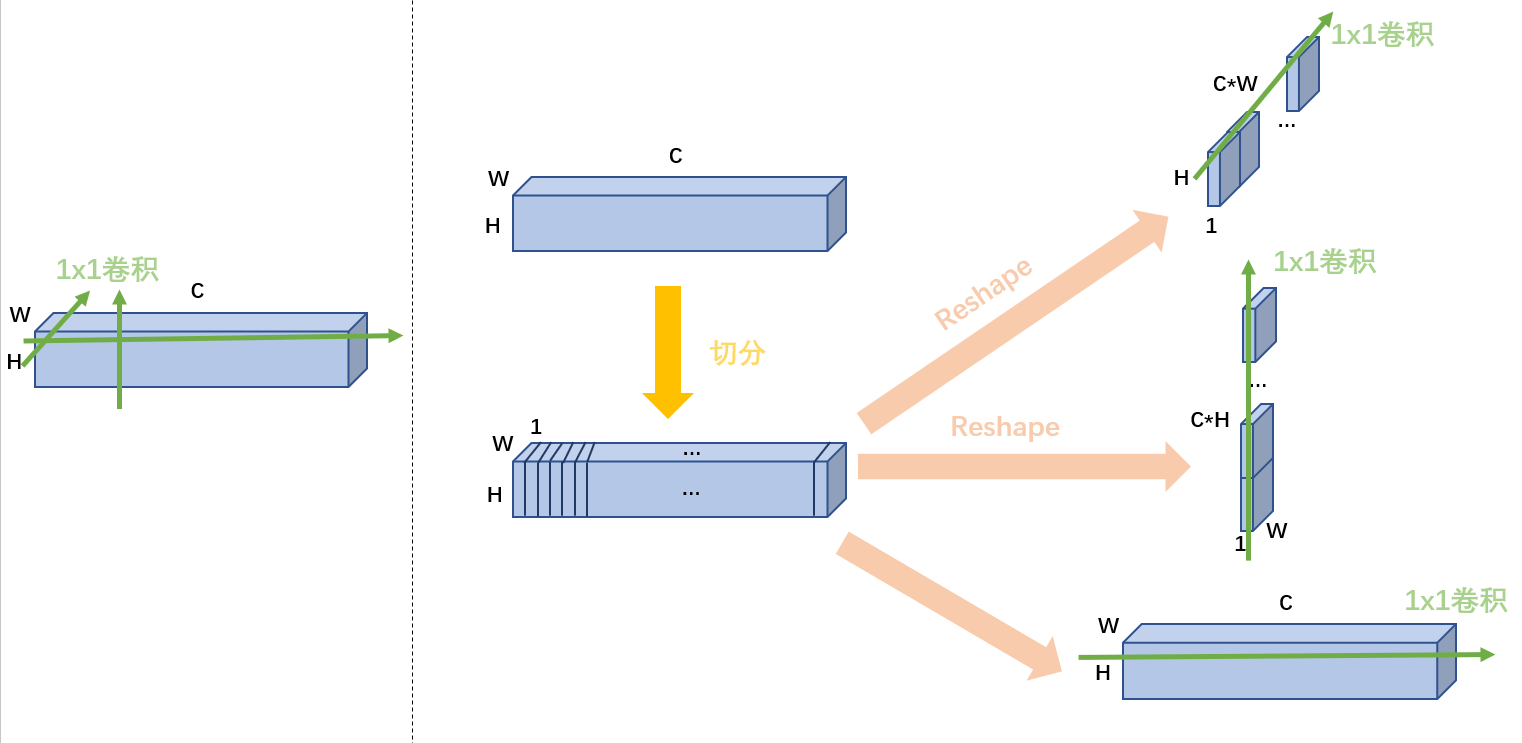
如果要考虑某一方向的固定位置的垂直方向感受野，应该按照如下图进行拆分才是的，为什么要拆成 S 组呢？我的理解是 nn.Linear(H*C, H*C) 和 nn.Linear(W*C, W*C) 的参数量太大了，直接 nn.Linear(H, H) 和 nn.Linear(W, W) 又太简单了，而且也与通道方向的 nn.Linear(C, C) 不匹配，所以进行了分组。

3.2 特征融合

如何将宽度方向、长度方向和通道方向独立建模的三个分支的结果进行整合呢？最简单粗暴的方法就是直接相加在经过一个全连接层。正如上面的伪代码所示。这样做可以，但是有点太简单了，或者说他就是加权求和的特殊情况。 $\hat{\mathbf{X}}=\mathrm{FC}\left(\mathbf{X}_{H}+\mathbf{X}_{W}+\mathbf{X}_{C}\right)$ 那么考虑加权求和是不是更好一点呢？当然！作者将之称为 Weighted Permute-MLP。实际上他就是使用了 ResNeSt 的 Split Attention （其实和 SE Block 有点像，SE block 是对特征图每个通道算权重，Split Attention 是对于多个三维特征图算每个三维特征图的权重）。

Split Attention 如下图所示，假设有 k 个 $H \times W \times C$ 的特征矩阵：

首先是对于各个特征矩阵元素求和得到一个 $H \times W \times C$ 的特征矩阵
然后按照空间内进行全局平均池化 (等价于直接求和)，将特征矩阵变为一个 C 维向量
然后经过两个全连接层 C–>C’–> kC，实现中作者将 C‘ 确定为 C//4，Dropout，BN，ReLU 等就不做叙述，并将全连接层的输出拆分为 k 个 C 维向量
进行 Softmax 得到每个特征矩阵对应的权重 (关于 nn.Softmax 使用可以参考 pytorch:nn.Softmax())，得到的结果就是第一个通道，k 个特征矩阵权重和为 1；第二个通道，k 个特征矩阵权重和为 1 等等…
将每个 Split Attention 模块输入的每个 Feature Map 和计算出来的每个 split 的权重相乘，再将结果加和，得到最终的结果

最终 Permutator 的实现可以表示为，这里忽略了激活函数。 $\begin{aligned} &\mathbf{Y}=\text {(Weighted) Permute-MLP }(\mathrm{LN}(\mathbf{X}))+\mathbf{X} \\ &\mathbf{Z}=\text { Channel-MLP }(\mathrm{LN}(\mathbf{Y}))+\mathbf{Y} \end{aligned}$

3.3 分支分析

Permute-MLP 层最大的特点在于其中包含了为宽度方向、长度方向和通道方向独立建模的三个分支，但是每个分支作用如何？作者进行了消融实验。下表实验发现，在 Permute-MLP 三个分支中将高度或者宽度分支替换为通道分支都会造成大幅度性能的下降 (7.8\% 和 7.9\%)，体现了两个方向信息相互补充聚合的必要性。此外，Split Attention 相比简单粗暴的元素求和带来了 0.4\% 的提升。但是，Split Attention 结构的影响不如训练过程中数据增强来得大…

4. 总结

对于 ViP 的一些反思：ViP 是一种用于视觉识别任务的概念简单、数据高效的类MLP架构。ViP 采用线性投影方式沿高与宽维度编码特征表达。这使的 ViP 能够沿单一空间维度捕获长距离依赖关系，同时沿另一个方向保持精确的位置信息，然后通过相互补充聚合方式产生位置敏感输出，进而形成关于目标区域的强有力表征。通过 Split Attention 进行信息整合也是很好的点。但提出的 Permutator 的一个明显的缺点是空间维度上的缩放问题，比如在 Permute-MLP 层中 N = W，这就使得 ViP 无法接受任意大小的图像输入。ViP 也没办法构成 Backbone 用于下游任务。ViP 使用的感受野也并非传统计算机视觉底层特征提取的建议感受野。

延续我一贯的认识，如何在 MLP 架构中如何结合图像局部性和长距离依赖依然是值得探讨的点。

### 5. 代码

代码来源详见此处。

import torch
import torch.nn as nn

from timm.data import IMAGENET_DEFAULT_MEAN, IMAGENET_DEFAULT_STD
from timm.models.layers import DropPath, trunc_normal_
from timm.models.registry import register_model

def _cfg(url='', **kwargs):
    return {
        'url': url,
        'num_classes': 1000, 'input_size': (3, 224, 224), 'pool_size': None,
        'crop_pct': .96, 'interpolation': 'bicubic',
        'mean': IMAGENET_DEFAULT_MEAN, 'std': IMAGENET_DEFAULT_STD, 'classifier': 'head',
        **kwargs
    }

default_cfgs = {
    'ViP_S': _cfg(crop_pct=0.9),
    'ViP_M': _cfg(crop_pct=0.9),
    'ViP_L': _cfg(crop_pct=0.875),
}


class Mlp(nn.Module):
    def __init__(self, in_features, hidden_features=None, out_features=None, act_layer=nn.GELU, drop=0.):
        super().__init__()
        out_features = out_features or in_features
        hidden_features = hidden_features or in_features
        self.fc1 = nn.Linear(in_features, hidden_features)
        self.act = act_layer()
        self.fc2 = nn.Linear(hidden_features, out_features)
        self.drop = nn.Dropout(drop)

    def forward(self, x):
        x = self.fc1(x)
        x = self.act(x)
        x = self.drop(x)
        x = self.fc2(x)
        x = self.drop(x)
        return x

class WeightedPermuteMLP(nn.Module):
    def __init__(self, dim, segment_dim=8, qkv_bias=False, qk_scale=None, attn_drop=0., proj_drop=0.):
        super().__init__()
        self.segment_dim = segment_dim

        self.mlp_c = nn.Linear(dim, dim, bias=qkv_bias)
        self.mlp_h = nn.Linear(dim, dim, bias=qkv_bias)
        self.mlp_w = nn.Linear(dim, dim, bias=qkv_bias)

        self.reweight = Mlp(dim, dim // 4, dim *3)
        
        self.proj = nn.Linear(dim, dim)
        self.proj_drop = nn.Dropout(proj_drop)



    def forward(self, x):
        B, H, W, C = x.shape

        S = C // self.segment_dim
        h = x.reshape(B, H, W, self.segment_dim, S).permute(0, 3, 2, 1, 4).reshape(B, self.segment_dim, W, H*S)
        h = self.mlp_h(h).reshape(B, self.segment_dim, W, H, S).permute(0, 3, 2, 1, 4).reshape(B, H, W, C)

        w = x.reshape(B, H, W, self.segment_dim, S).permute(0, 1, 3, 2, 4).reshape(B, H, self.segment_dim, W*S)
        w = self.mlp_w(w).reshape(B, H, self.segment_dim, W, S).permute(0, 1, 3, 2, 4).reshape(B, H, W, C)

        c = self.mlp_c(x)
        
        a = (h + w + c).permute(0, 3, 1, 2).flatten(2).mean(2)
        a = self.reweight(a).reshape(B, C, 3).permute(2, 0, 1).softmax(dim=0).unsqueeze(2).unsqueeze(2)

        x = h * a[0] + w * a[1] + c * a[2]

        x = self.proj(x)
        x = self.proj_drop(x)

        return x


class PermutatorBlock(nn.Module):

    def __init__(self, dim, segment_dim, mlp_ratio=4., qkv_bias=False, qk_scale=None, drop=0., attn_drop=0.,
                 drop_path=0., act_layer=nn.GELU, norm_layer=nn.LayerNorm, skip_lam=1.0, mlp_fn = WeightedPermuteMLP):
        super().__init__()
        self.norm1 = norm_layer(dim)
        self.attn = mlp_fn(dim, segment_dim=segment_dim, qkv_bias=qkv_bias, qk_scale=None, attn_drop=attn_drop)

        # NOTE: drop path for stochastic depth, we shall see if this is better than dropout here
        self.drop_path = DropPath(drop_path) if drop_path > 0. else nn.Identity()

        self.norm2 = norm_layer(dim)
        mlp_hidden_dim = int(dim * mlp_ratio)
        self.mlp = Mlp(in_features=dim, hidden_features=mlp_hidden_dim, act_layer=act_layer)
        self.skip_lam = skip_lam

    def forward(self, x):
        x = x + self.drop_path(self.attn(self.norm1(x))) / self.skip_lam
        x = x + self.drop_path(self.mlp(self.norm2(x))) / self.skip_lam
        return x

class PatchEmbed(nn.Module):
    """ Image to Patch Embedding
    """
    def __init__(self, img_size=224, patch_size=16, in_chans=3, embed_dim=768):
        super().__init__()
        self.proj = nn.Conv2d(in_chans, embed_dim, kernel_size=patch_size, stride=patch_size)

    def forward(self, x):
        x = self.proj(x) # B, C, H, W
        return x


class Downsample(nn.Module):
    """ Image to Patch Embedding
    """
    def __init__(self, in_embed_dim, out_embed_dim, patch_size):
        super().__init__()
        self.proj = nn.Conv2d(in_embed_dim, out_embed_dim, kernel_size=patch_size, stride=patch_size)

    def forward(self, x):
        x = x.permute(0, 3, 1, 2)
        x = self.proj(x) # B, C, H, W
        x = x.permute(0, 2, 3, 1)
        return x

def basic_blocks(dim, index, layers, segment_dim, mlp_ratio=3., qkv_bias=False, qk_scale=None, \
    attn_drop=0, drop_path_rate=0., skip_lam=1.0, mlp_fn = WeightedPermuteMLP, **kwargs):
    blocks = []

    for block_idx in range(layers[index]):
        block_dpr = drop_path_rate * (block_idx + sum(layers[:index])) / (sum(layers) - 1)
        blocks.append(PermutatorBlock(dim, segment_dim, mlp_ratio=mlp_ratio, qkv_bias=qkv_bias, qk_scale=qk_scale,\
            attn_drop=attn_drop, drop_path=block_dpr, skip_lam=skip_lam, mlp_fn = mlp_fn))

    blocks = nn.Sequential(*blocks)

    return blocks

class VisionPermutator(nn.Module):
    """ Vision Permutator
    """
    def __init__(self, layers, img_size=224, patch_size=4, in_chans=3, num_classes=1000,
        embed_dims=None, transitions=None, segment_dim=None, mlp_ratios=None, skip_lam=1.0,
        qkv_bias=False, qk_scale=None, drop_rate=0., attn_drop_rate=0., drop_path_rate=0.,
        norm_layer=nn.LayerNorm,mlp_fn = WeightedPermuteMLP):

        super().__init__()
        self.num_classes = num_classes

        self.patch_embed = PatchEmbed(img_size = img_size, patch_size=patch_size, in_chans=in_chans, embed_dim=embed_dims[0])

        network = []
        for i in range(len(layers)):
            stage = basic_blocks(embed_dims[i], i, layers, segment_dim[i], mlp_ratio=mlp_ratios[i], qkv_bias=qkv_bias,
                    qk_scale=qk_scale, attn_drop=attn_drop_rate, drop_path_rate=drop_path_rate, norm_layer=norm_layer, skip_lam=skip_lam,
                    mlp_fn = mlp_fn)
            network.append(stage)
            if i >= len(layers) - 1:
                break
            if transitions[i] or embed_dims[i] != embed_dims[i+1]:
                patch_size = 2 if transitions[i] else 1
                network.append(Downsample(embed_dims[i], embed_dims[i+1], patch_size))


        self.network = nn.ModuleList(network)

        self.norm = norm_layer(embed_dims[-1])

        # Classifier head
        self.head = nn.Linear(embed_dims[-1], num_classes) if num_classes > 0 else nn.Identity()
        self.apply(self._init_weights)

    def _init_weights(self, m):
        if isinstance(m, nn.Linear):
            trunc_normal_(m.weight, std=.02)
            if isinstance(m, nn.Linear) and m.bias is not None:
                nn.init.constant_(m.bias, 0)
        elif isinstance(m, nn.LayerNorm):
            nn.init.constant_(m.bias, 0)
            nn.init.constant_(m.weight, 1.0)

    def get_classifier(self):
        return self.head

    def reset_classifier(self, num_classes, global_pool=''):
        self.num_classes = num_classes
        self.head = nn.Linear(self.embed_dim, num_classes) if num_classes > 0 else nn.Identity()

    def forward_embeddings(self, x):
        x = self.patch_embed(x)
        # B,C,H,W-> B,H,W,C
        x = x.permute(0, 2, 3, 1)
        return x

    def forward_tokens(self,x):
        for idx, block in enumerate(self.network):
            x = block(x)
        B, H, W, C = x.shape
        x = x.reshape(B, -1, C)
        return x

    def forward(self, x):
        x = self.forward_embeddings(x)
        # B, H, W, C -> B, N, C
        x = self.forward_tokens(x)
        x = self.norm(x)
        return self.head(x.mean(1))




@register_model
def vip_s14(pretrained=False, **kwargs):
    layers = [4, 3, 8, 3]
    transitions = [False, False, False, False]
    segment_dim = [16, 16, 16, 16]
    mlp_ratios = [3, 3, 3, 3]
    embed_dims = [384, 384, 384, 384]
    model = VisionPermutator(layers, embed_dims=embed_dims, patch_size=14, transitions=transitions,
        segment_dim=segment_dim, mlp_ratios=mlp_ratios, mlp_fn=WeightedPermuteMLP, **kwargs)
    model.default_cfg = default_cfgs['ViP_S']
    return model

@register_model
def vip_s7(pretrained=False, **kwargs):
    layers = [4, 3, 8, 3]
    transitions = [True, False, False, False]
    segment_dim = [32, 16, 16, 16]
    mlp_ratios = [3, 3, 3, 3]
    embed_dims = [192, 384, 384, 384]
    model = VisionPermutator(layers, embed_dims=embed_dims, patch_size=7, transitions=transitions,
        segment_dim=segment_dim, mlp_ratios=mlp_ratios, mlp_fn=WeightedPermuteMLP, **kwargs)
    model.default_cfg = default_cfgs['ViP_S']
    return model

@register_model
def vip_m7(pretrained=False, **kwargs):
    # 55534632
    layers = [4, 3, 14, 3]
    transitions = [False, True, False, False]
    segment_dim = [32, 32, 16, 16]
    mlp_ratios = [3, 3, 3, 3]
    embed_dims = [256, 256, 512, 512]
    model = VisionPermutator(layers, embed_dims=embed_dims, patch_size=7, transitions=transitions,
        segment_dim=segment_dim, mlp_ratios=mlp_ratios, mlp_fn=WeightedPermuteMLP, **kwargs)
    model.default_cfg = default_cfgs['ViP_M']
    return model


@register_model
def vip_l7(pretrained=False, **kwargs):
    layers = [8, 8, 16, 4]
    transitions = [True, False, False, False]
    segment_dim = [32, 16, 16, 16]
    mlp_ratios = [3, 3, 3, 3]
    embed_dims = [256, 512, 512, 512]
    model = VisionPermutator(layers, embed_dims=embed_dims, patch_size=7, transitions=transitions,
        segment_dim=segment_dim, mlp_ratios=mlp_ratios, mlp_fn=WeightedPermuteMLP, **kwargs)
    model.default_cfg = default_cfgs['ViP_L']
    return model