深度学习之图像分类（二十三）-- S2MLP网络详解

深度学习之图像分类（二十三）S2MLP网络详解

在上一讲 AS-MLP 中，我们发现该工作和百度的 S2MLP 接近，为此本节我们便来学习学习 S2MLP 的基本思想，其想将图像的局部性融入纯 MLP 结构中去。

1. 前言

S2MLP 是百度提出的用于视觉的空间位移 MLP 架构，论文为 S2 -MLP: Spatial-Shift MLP Architecture for Vision。MLP-Mixer 好在它进一步去除了归纳偏置（即CNN的局部性和Transformer 的注意力机制），使用纯 MLP 架构进行学习，该工作这出在超大规模数据量训练时可以取得和 CNN 以及 Transformer 结构相当甚至更好的性能。然而，单单在 ImageNet 1k 或者 ImageNet 21K 上训练测试，其性能其实并不算太好。这是为什么呢？因为虽然 MLP-Mixer 增加了学习的自由性，没有给予局部性啊这些的约束，但是正因如此才更容易过拟合（But the freedom from breaking a chain is accompanied by the risk of over-fitting）。所以只有当它在超大规模数据量的训练下才可能变得普适。为此，我们实际上还是得给一些约束或者指导，以帮助模型在中小规模数据上训练得更好。

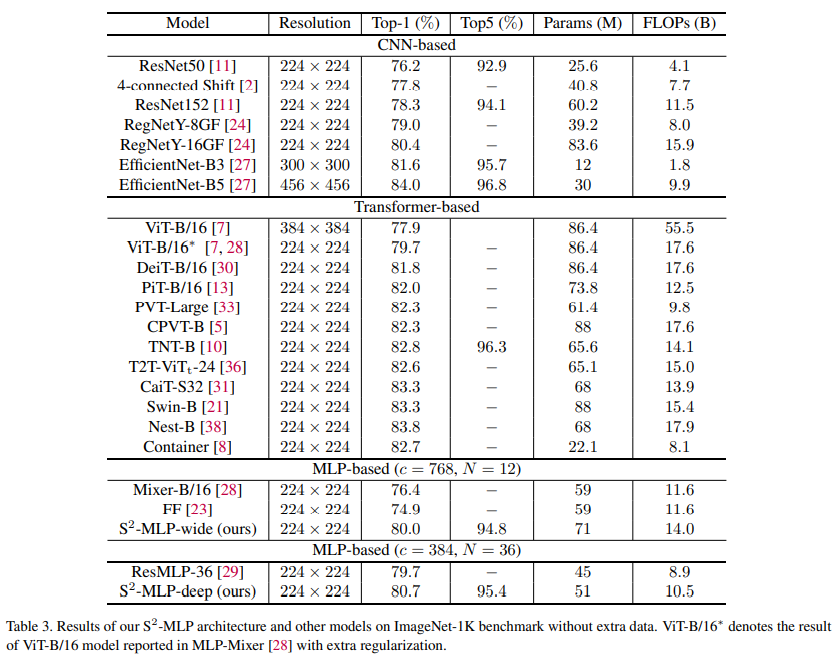
S2MLP 取消了 MLP-Mixer 中的 token-mixing MLP，仅仅保留 channel-minxing MLP，并且通过空间位移（Spatial-shift）操作将不同位置的特征移动到同一个通道对齐，从而在 channel-minxing MLP 中获得局部感受野的概念（token-mixing MLP是全局感受野的概念）。与 AS-MLP 不同之处在于没有更进一步把它构建为 Backbone，感受野的故事也不是特别诱人。实现发现，S2MLP 相较于 MLP-Mixer 性能有一定提升，但是对于 CNN 以及 Transformer-based 还是有一定的差距。

2. S2MLP 网络结构

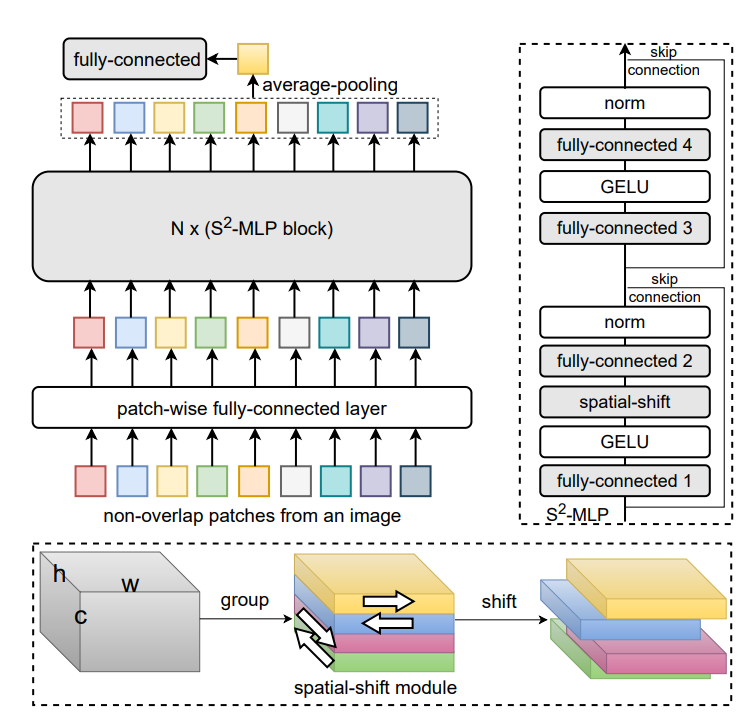
S2MLP 和 MLP-Mixer 类似，整体网络结构如下图所示，其中 S2MLP block 被重复了多次。我们先来全局性地讲一下 S2MLP 怎么工作的：

• 首先是对于一个 $3 \times H \times W$ 的输入 RGB 图像，将其进行 patch 切片，patch 大小为 $p \times p$，patch 的个数为 $\frac{H}{p} \times \frac{W}{p}$，并将 patch 展平为一个向量，维度为 $3p^2$。然后经过一个 patch-wise fully-connected layer (其实也就是 $1 \times 1$ 卷积)，将 $3p^2$ 降维为 $c$。在全连接层后有一个 LN 层进行归一化。令 $h = \frac{H}{p}, w = \frac{W}{p}$，此时我们就有 $h \times w \times c$ 的一个矩阵。作者使用过程中 $p = 16$，此时 $h \times w = 192$。
• 随后 $h \times w \times c$ 的特征图被视为 $h \times w$ 个 token，每个 token 的维度为 $c$。之后经过 N 个 S2MLP block，其中每个 Block 包含了四个全连接层，两个残差结构，两个 GELU 激活函数，两个 LN 归一化层，以及一个 Spatial-shift 操作，这些配置和 MLP-Mixer 是一致的，唯一的不同就是把 token-mixing MLP 中两个全连接层替换为了通道方向全连接再经过 Spatial-shift 操作之后再通道方向全连接。值得注意的是，fully-connected 3 全连接层通常会对节点数进行扩充，再通过 fully-connected 4 还原回来。这里 fully-connected 3 的 expansion ratio 被设置为 4（与 ViT 等工作的设置一致）。
• 最后的输出结果经过全局平均池化和全连接层，就可以得到输出了。

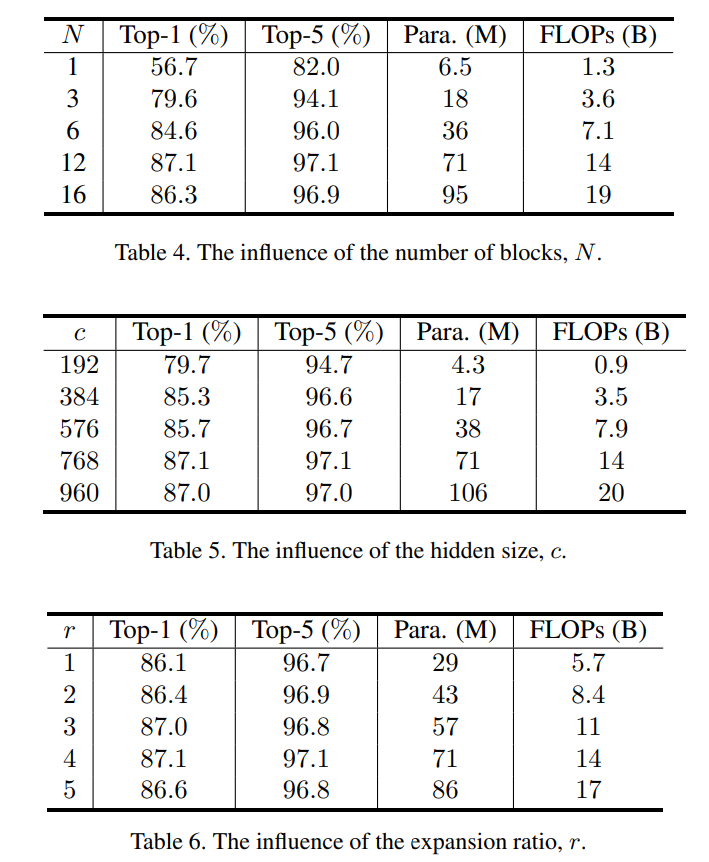
两个不同配置的 S2MLP 网络的配置表如下，一种为宽的 (每个 token 的 c 更大)，一种为深的（S2MLP block 被重复的次数 N 更多）

不难预料，最终的共性都是 $r,c,N$ 先增加时，网络性能更好，然后不能太大，否则又会变差。并且也需要权衡参数量(Para)和计算量(FLOPs)。

3. S2MLP Block

3.1 Block 结构

在对 S2MLP 网络整体有个概念后，我们来看看单个 Block 是怎么设计的。

• 首先是特征图输入后，对 Channel 进行一个全连接，这里是对于特定位置信息进行交流，其实也就是 $1 \times 1$ 卷积。然后经过一个 GELU 激活函数。
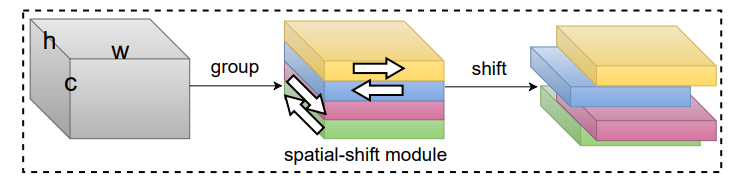
• 其次对特征图进行 Spatial-shift 操作，这是一个固定的操作无需参数，并且四个方向都包含使得其是各向同性的。具体而言将特征图按通道分为 4 个组（和组卷积的定义一样），然后第一个组水平右移一个单位，第二组水平左移一个单位，第三组竖直下移一个单位，第四组竖直上移一个单位。通过简单的赋值就可以实现。并且 padding 为保留原始值（padding 在 AS-MLP 中被证明 Zero-padding 也是极好的）。这样就实现了不同位置的特征移动到同一个通道处对齐。然后再经过一个全连接层，其实也就是 $1 \times 1$ 卷积，进行局部感受野信息的融合，来实现不同 patch 之间的通信。此后经过一个 LN 归一化和残差（注意，这里不激活了，其实仔细去看哈，激活和归一化的位置和 MLP-Mixer 是一致的）。

def spatial_shift(x):
    w,h,c = x.size()
    x[1:,:,:c/4] = x[:w-1,:,:c/4]
    x[:w-1,:,c/4:c/2] = x[1:,:,c/4:c/2]
    x[:,1:,c/2:c*3/4] = x[:,:h-1,c/2:c*3/4]
    x[:,:h-1,3*c/4:] = x[:,1:,3*c/4:]
    return x

• 接下来的全连接，GELU，全连接，LN 其实就是和 MLP-Mixer 中的 Channel-mixing MLP 一致。

3.2 Spatial-shift 操作

空间位移操作其实就是把特征图按照不同方向进行了平移。这等价于一个卷积操作。即前 $c/4$ 个通道每个通道特征图卷积 $K_i$， $c/4$ 到 $c/2$ 通道每个通道特征图卷积 $K_j$， $c/2$ 到 $3c/4$ 通道每个通道特征图卷积 $K_k$， $3c/4$ 到 $c$ 通道每个通道特征图卷积 $K_l$。 \(\begin{aligned} &\mathcal{T}_{1}[1: w,:,:] \leftarrow \mathcal{T}_{1}[0: w-1,:,:] \\ &\mathcal{T}_{2}[0: w-1,:,:] \leftarrow \mathcal{T}_{2}[1: w,:,:] \\ &\mathcal{T}_{3}[:, 1: h,:] \leftarrow \mathcal{T}_{3}[:, 0: h-1,:], \\ &\mathcal{T}_{4}\left[:, 0: h-1,: \mid \leftarrow \mathcal{T}_{4}[:, 1: h,: \mid .\right. \end{aligned}\)

不难发现，$(x,y)$ 处最终会有 $(x-1,y),(x,y-1),(x+1,y),(x,y+1)$ 四个地方的特征图移动过来，所以说最终的感受野是菱形，注意不是 AS-MLP 的十字形。因为它没有不移动的特征图（在 S2MLPv2 中会加，我们之后学习博客中会讲到）！实现不同 patch 之间的通信，其实少了中间，这个感受野似乎并不是那么完美。

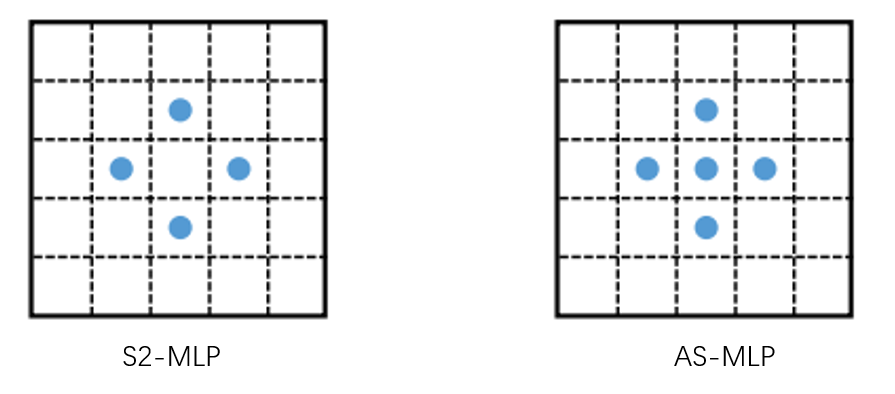
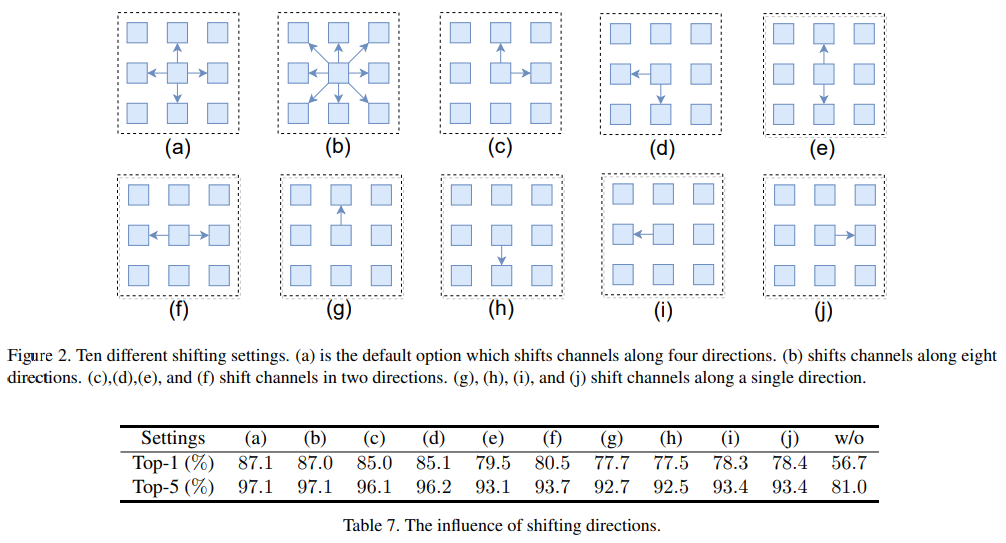
作者对比了不同的 spatial-shift 操作，其对应的移动和结果如下图所示，最终发现 (a) 的效果是最好的。但是我觉得作者如果加上有一个不移动可能会更好！

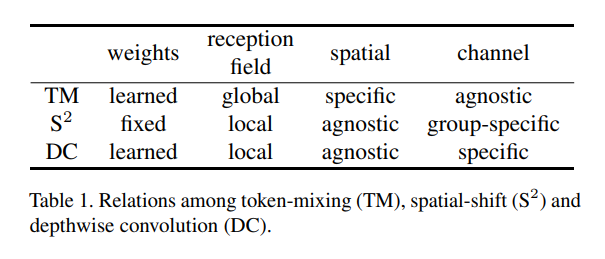
那么在此基础上，Token-mixing MLP，spatial-shift 操作以及 通道可分离卷积 depthwise convolution 之间的关系是什么呢？

• spatial-shift 操作是固定权重的，其余二者是可学习的
• spatial-shift 操作以及 DW 都是局部感受野，Token-mixing MLP 是全局感受野
• spatial-shift 操作以及 DW 对空间不敏感，而 Token-mixing MLP 对空间是敏感的
• Token-mixing MLP 在通道上是一致的，DC 的卷积核每个通道是互异的，spatial-shift 操作可被视为一种特殊的组卷积，即一组内的卷积核是一样的

5. 总结

对于 S2MLP 的一些反思：S2MLP 比 AS-MLP 更早挂上，也是向 MLP 架构中引入局部性特性。做法其实很简单，在 ImageNet1k 数据集上能 work 也很自然（这个数据量不足以让 MLP-Mixer 学会普适的表示）。但是，就 S2MLPv1 而言，其贡献点还是薄弱，不仅性能不是特别出彩；对于感受野的扩展性以及设计也不足；此外，都使用了对空间不敏感的 spatial-shift 操作以及 channel-mixing MLP 了，没有更进一步推出下游任务的 backbone 是比较可惜的点。相比而言，S2MLPv2 结合了 S2MLPv1 和 ViP 的思想，会更值得关注。所以下一篇学习的就是 ViP，再下一篇就是学习 S2MLPv2。

延续我一贯的认识，如何在 MLP 架构中如何结合图像局部性和长距离依赖依然是值得探讨的点。

### 6. 代码

暂未开源，保持关注…