深度学习之目标检测(九)YOLOv3 SPP理论介绍
本章学习 YOLO v3 SPP 相关理论知识,学习视频源于 Bilibili。本章节基于 ultralytics 版本的 YOLOv3 进行讲解。项目中作者使用了非常多的 trick,包括图像增强,SPP,CIOU Loss。至于 Focal loss 虽然作者实现了,但是没有去使用它,因为效果并不是特别好。所以默认不去启用他。
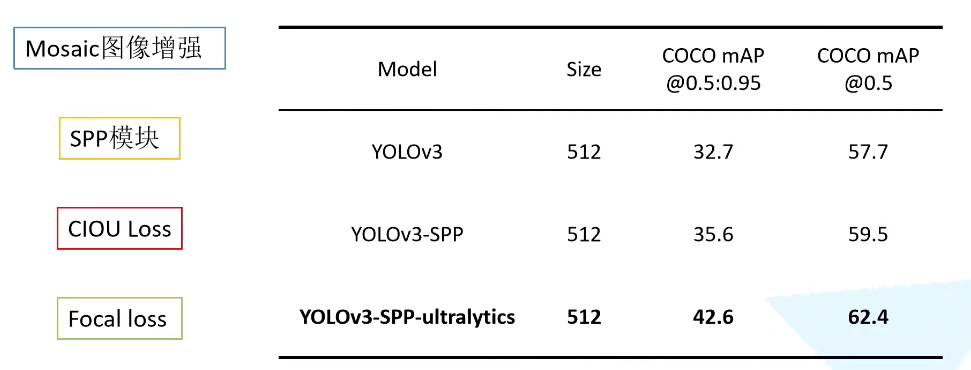
基于 ultralytics 版本的 YOLOv3 SPP 整个网络结构如下图所示,以 $512 \times 512$ 为输入尺寸进行绘制的,下图源于 此处。
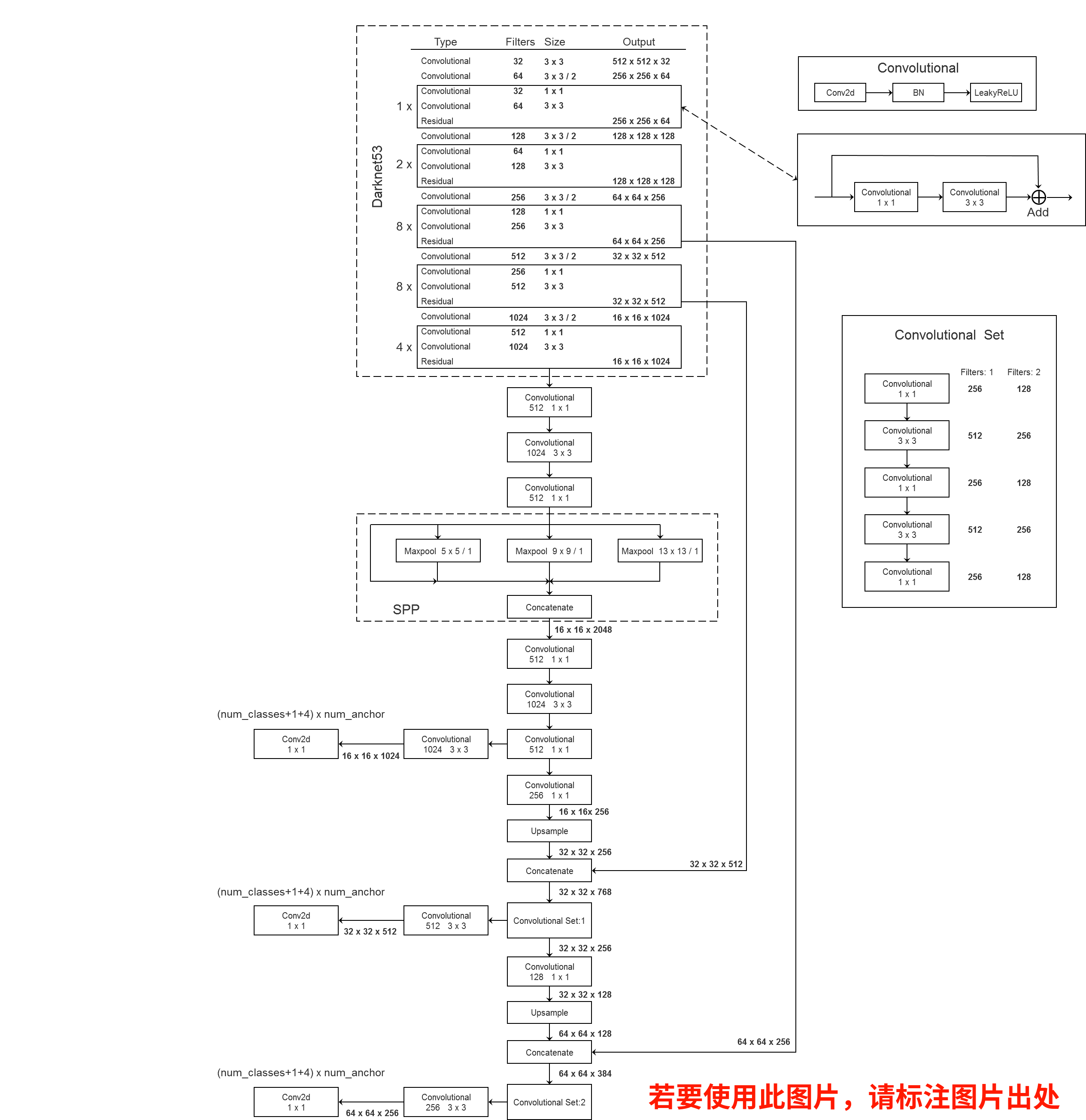
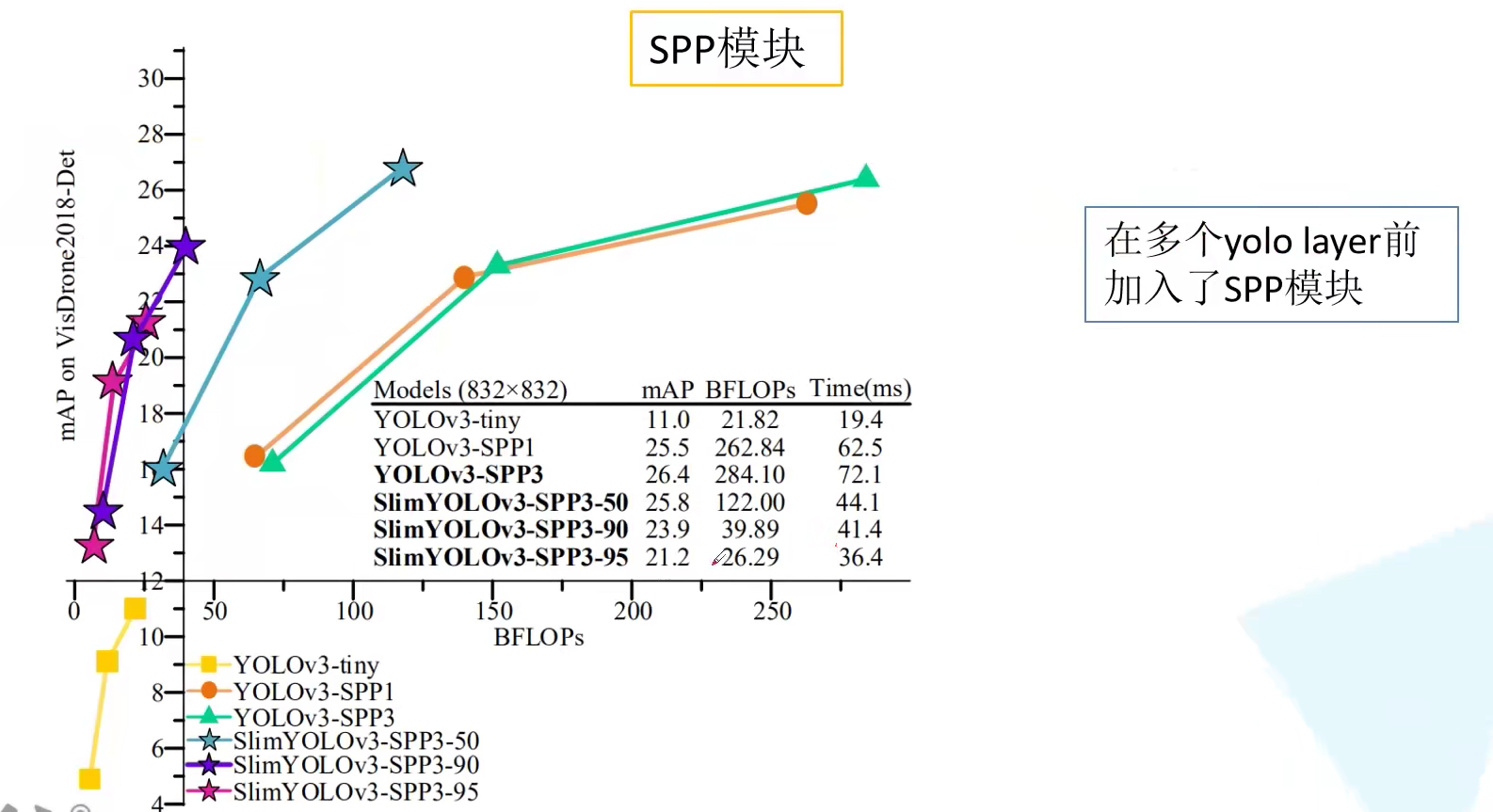
与 YOLOv3 的区别在于,将第一个预测特征图经过的 Convolution Set 给从中间拆开插入了 SPP 模块。
1. Mosaic 图像增强
将多张图片拼接在一起输入给网络进行训练的过程。在源码中默认使用 4 张图片进行拼接,进行预测。
- 增加了数据的多样性
- 增加了目标的个数
- BN 能一次性统计多张图片的参数 (BN 层 batchsize 尽可能大一点,所求的均值方差越接近数据集,效果更好。如果拼接多张图其实等效并行输入多张原始图像)
2. SPP 模块
YOLOv3 中的 SPP 模块并不是 SPPnet 的 SPP 结构 (Spatial Pyramid Pooling),有所借鉴但是不同。SPP 模块很简单,首先输入直接接到输出作为第一个分支,第二个分支是池化核为 $5 \times 5$ 的最大池化,第二个分支是池化核为 $9 \times 9$ 的最大池化,第四个分支是池化核为 $13 \times 13$ 的最大池化,注意步距都是为 1,意味着池化前进行 padding 填充,最后池化后得到的特征图尺寸大小和深度不变。SPP 模块实现了不同尺度特征的融合。
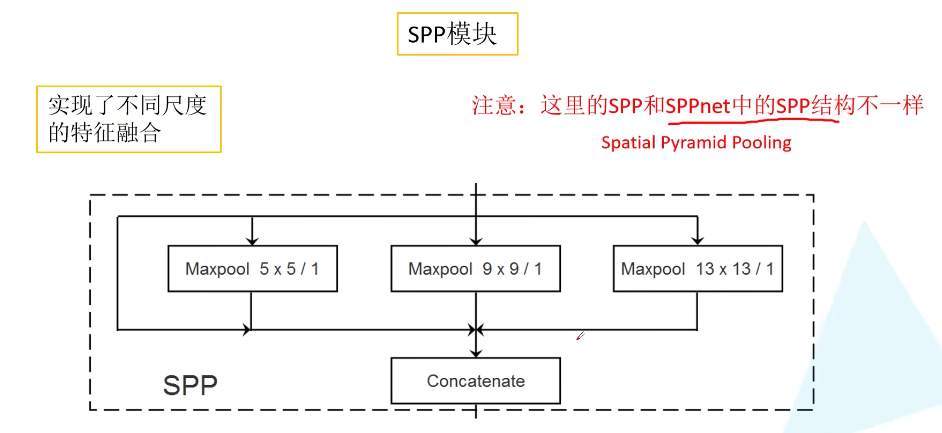
SPP 模块的输入为 $16 \times 16 \times 512$,其输出为 $16 \times 16 \times 2048$,即深度扩充了 4 倍。
为什么第一个预测特征层前接了 SPP 结构呢?在第二、三个预测特征层前接上 SPP 结构会怎么样呢?
从下图可见,YOLOv3-SPP1 和 YOLOv3-SPP3 的性能相近。实验结果发现,当输入尺度小的时候 YOLOv3-SPP1 还会好一点,但是随着输入尺度的增大,YOLOv3-SPP3 的性能会略好一点。
3. CIoU Loss
推荐博文:https://zhuanlan.zhihu.com/p/94799295
过去的边界框损失计算就是差值的平方,也就是 L2 损失。这里我们讲 IoU 损失的发展历程,其中 DIoU Loss 和 CIoU Loss 是在同一篇论文发表的。作为损失函数通常需要考虑几个方面:非负性;同一性;对称性;三角不等性。
3.1 IoU Loss
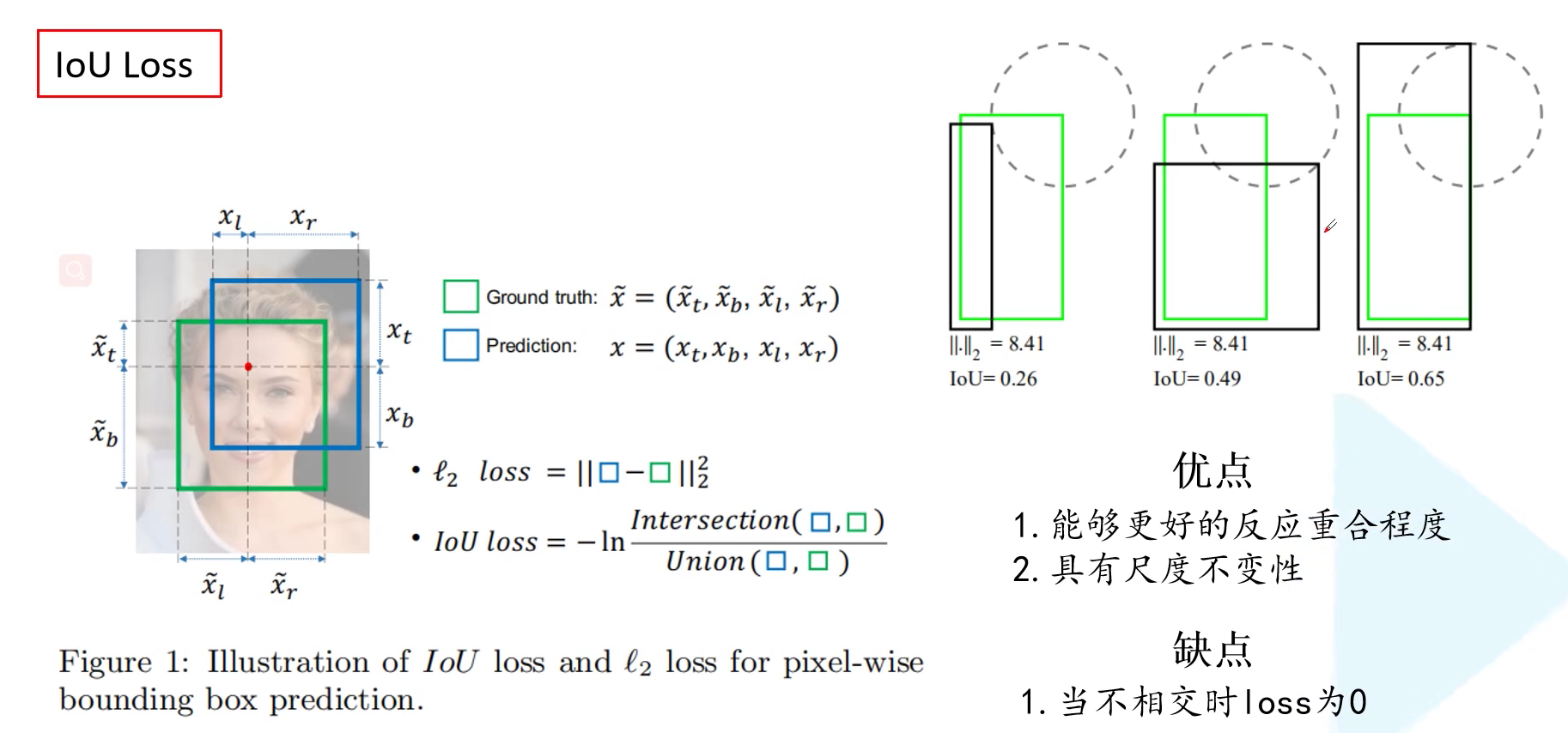
我们在下图右上角展示了三组预测示例,可以看出来第三个的矩形框预测效果相对较好。计算它们的 L2 损失其实是一样的,但是 IoU 值不同。说明 L2 损失不能很好反映目标边界框预测的重合程度。同时 L2 损失还对边界框尺寸比较敏感。IoU loss = -ln(iou)。还有一个更加常见的计算公式则是 IoU Loss = 1 - iou。IoU Loss 可以更好地反映出重合程度;且具有尺度不变性,无论重叠地框是大是小,重叠占比一定 IoU 一样大 。但是当预测框和 GT 框不重叠时,损失为 0。
import numpy as np
def Iou(box1, box2, wh=False):
if wh == False:
xmin1, ymin1, xmax1, ymax1 = box1
xmin2, ymin2, xmax2, ymax2 = box2
else:
xmin1, ymin1 = int(box1[0]-box1[2]/2.0), int(box1[1]-box1[3]/2.0)
xmax1, ymax1 = int(box1[0]+box1[2]/2.0), int(box1[1]+box1[3]/2.0)
xmin2, ymin2 = int(box2[0]-box2[2]/2.0), int(box2[1]-box2[3]/2.0)
xmax2, ymax2 = int(box2[0]+box2[2]/2.0), int(box2[1]+box2[3]/2.0)
# 获取矩形框交集对应的左上角和右下角的坐标(intersection)
xx1 = np.max([xmin1, xmin2])
yy1 = np.max([ymin1, ymin2])
xx2 = np.min([xmax1, xmax2])
yy2 = np.min([ymax1, ymax2])
# 计算两个矩形框面积
area1 = (xmax1-xmin1) * (ymax1-ymin1)
area2 = (xmax2-xmin2) * (ymax2-ymin2)
inter_area = (np.max([0, xx2-xx1])) * (np.max([0, yy2-yy1])) #计算交集面积
iou = inter_area / (area1+area2-inter_area+1e-6) #计算交并比
return iou
(参考 IoU 代码实现 https://zhuanlan.zhihu.com/p/94799295)
3.2 GIoU Loss
GIoU 原始论文为 Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression,在下图中绿色为真实目标边界框,红色为网络预测的目标边界框,蓝色是能框住真实边界框和预测边界框的最小矩形。Generalized IoU 公式如下所示,式中的 $A^c$ 即代表蓝色目标边界框的面积,$u$ 则是两个目标边界框并集的面积。注意是并集不是交集,是那个大的区域。当两个框完美重合的时候,$A^c = u$,GIoU = 1。当二者相距无穷远的时候,IoU = 0,$A^c » u$,GIoU = -1、
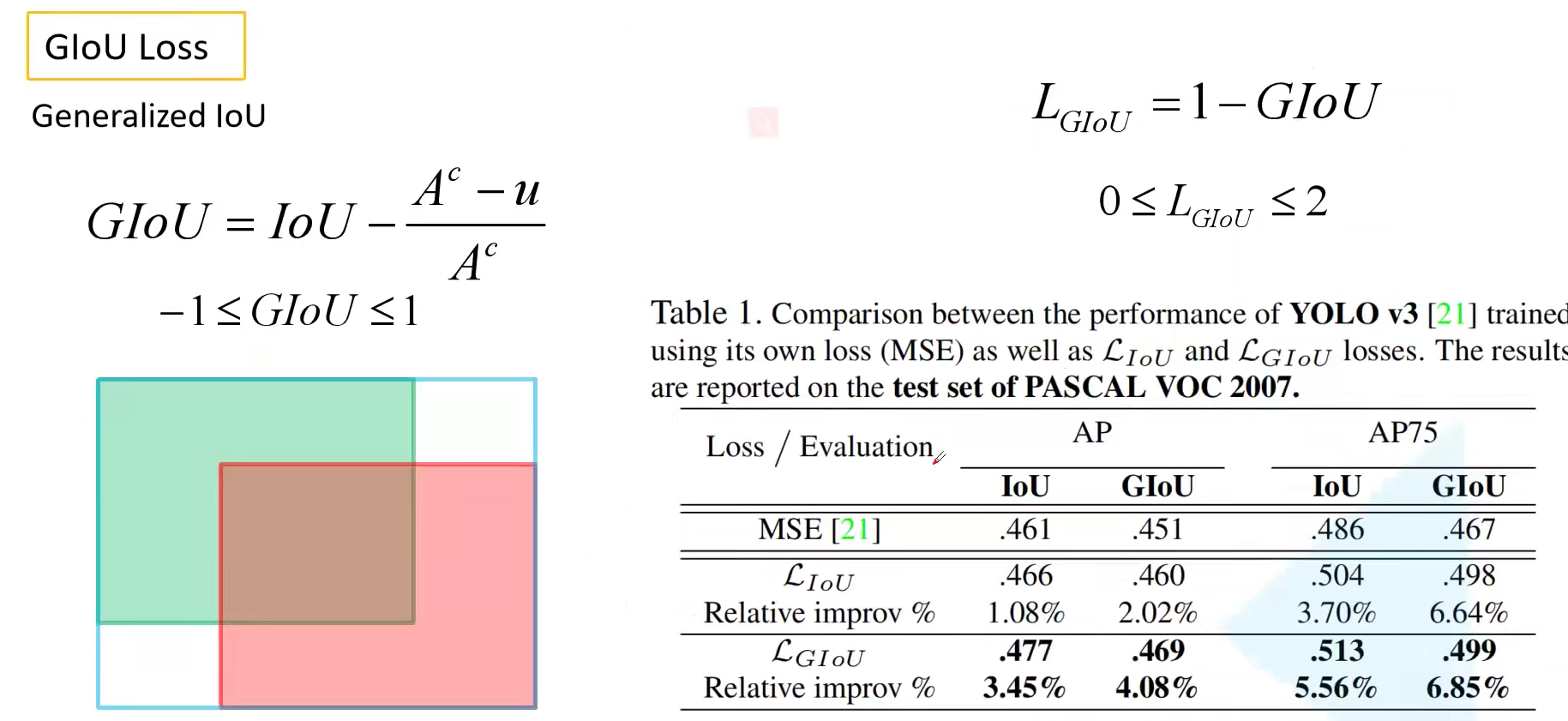
与IoU只关注重叠区域不同,GIoU不仅关注重叠区域,还关注其他的非重合区域,能更好的反映两者的重合度。然而,当真实边界框和预测边界框水平或者垂直重叠的时候,GIoU 就退化为了 IoU。
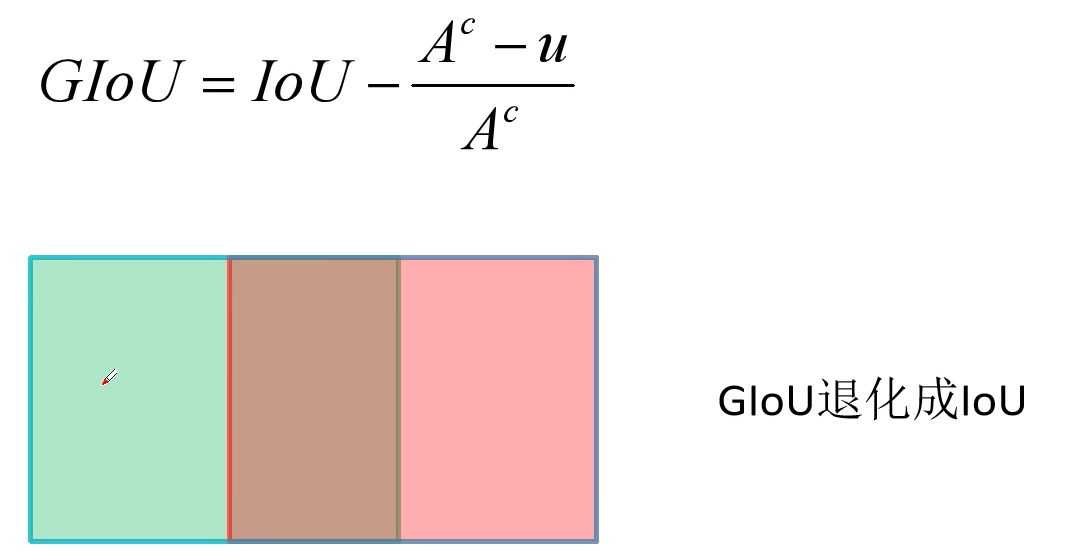
def Giou(rec1,rec2):
#分别是第一个矩形左右上下的坐标
x1,x2,y1,y2 = rec1
x3,x4,y3,y4 = rec2
iou = Iou(rec1,rec2)
area_C = (max(x1,x2,x3,x4)-min(x1,x2,x3,x4))*(max(y1,y2,y3,y4)-min(y1,y2,y3,y4))
area_1 = (x2-x1)*(y1-y2)
area_2 = (x4-x3)*(y3-y4)
sum_area = area_1 + area_2
w1 = x2 - x1 #第一个矩形的宽
w2 = x4 - x3 #第二个矩形的宽
h1 = y1 - y2
h2 = y3 - y4
W = min(x1,x2,x3,x4)+w1+w2-max(x1,x2,x3,x4) #交叉部分的宽
H = min(y1,y2,y3,y4)+h1+h2-max(y1,y2,y3,y4) #交叉部分的高
Area = W*H #交叉的面积
add_area = sum_area - Area #两矩形并集的面积
end_area = (area_C - add_area)/area_C #闭包区域中不属于两个框的区域占闭包区域的比重
giou = iou - end_area
return giou
(参考 GIoU 代码实现 https://zhuanlan.zhihu.com/p/94799295)
3.3 DIoU Loss
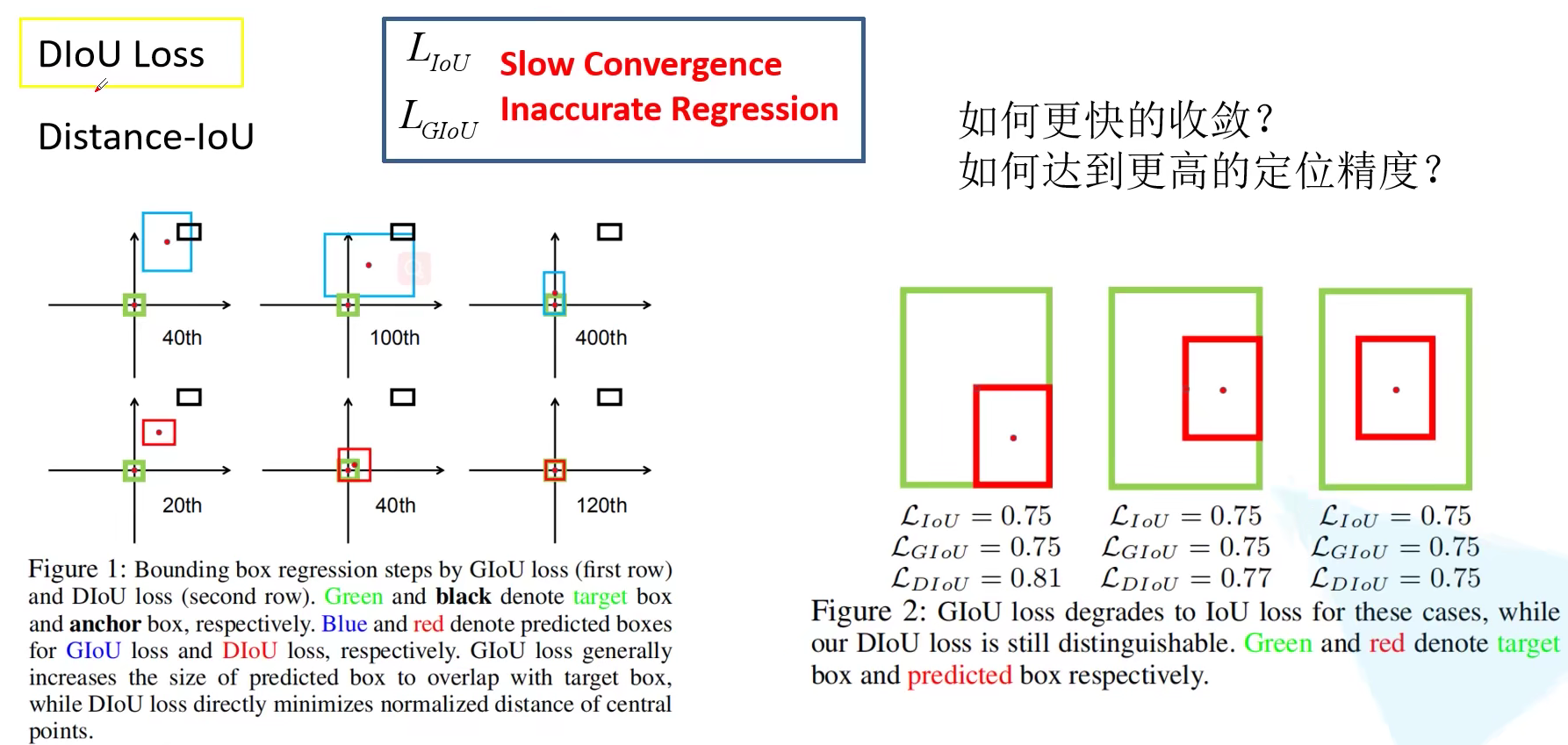
Distance-IoU 论文为 Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression,作者指出 IoU Loss 和 GIoU Loss 的两大问题是(1)收敛特别慢(2)回归还不够准确。首先看左边的图,上面一行就是使用 GIoU 来训练网络,下面是使用 DIoU 来训练网络。黑色代表的是 Anchor 或者说 Default box,绿色是真实目标边界框。我们希望蓝色、红色部分与真实目标边界框重合到一起。右边的图则针对三组预测目标和真是目标计算的IoU Loss。他们的 IoU Loss 和 GIoU Loss 一样(GIoU 已经退化为了 IoU),表现出 GIoU 在某些场景下不能很好表达目标边界框之间的重合位置关系。
DIoU 的计算公式如下所示, $b$ 与 $b^{gt}$ 分别表示预测边界框和真是边界框的中心位置,分子表示它们之间的欧氏距离,分母则表示能框住真实边界框和预测边界框的最小矩形的对角线距离的平方。当两个边界框完美重合的时候,$d = 0$,DIoU = 1;当两个边界框相距无穷远的时候,$d \approx c$,IoU = 0,DIoU = -1。DIoU 损失能直接最小化两个边界框之间的距离,因此收敛速度更快,回归更准确。DIoU 要比 GIou 更加符合目标框回归的机制,将目标与anchor之间的距离,重叠率以及尺度都考虑进去,使得目标框回归变得更加稳定,不会像 IoU 和 GIoU 一样出现训练过程中发散等问题。

def Diou(bboxes1, bboxes2):
rows = bboxes1.shape[0]
cols = bboxes2.shape[0]
dious = torch.zeros((rows, cols))
if rows * cols == 0:#
return dious
exchange = False
if bboxes1.shape[0] > bboxes2.shape[0]:
bboxes1, bboxes2 = bboxes2, bboxes1
dious = torch.zeros((cols, rows))
exchange = True
# #xmin,ymin,xmax,ymax->[:,0],[:,1],[:,2],[:,3]
w1 = bboxes1[:, 2] - bboxes1[:, 0]
h1 = bboxes1[:, 3] - bboxes1[:, 1]
w2 = bboxes2[:, 2] - bboxes2[:, 0]
h2 = bboxes2[:, 3] - bboxes2[:, 1]
area1 = w1 * h1
area2 = w2 * h2
center_x1 = (bboxes1[:, 2] + bboxes1[:, 0]) / 2
center_y1 = (bboxes1[:, 3] + bboxes1[:, 1]) / 2
center_x2 = (bboxes2[:, 2] + bboxes2[:, 0]) / 2
center_y2 = (bboxes2[:, 3] + bboxes2[:, 1]) / 2
inter_max_xy = torch.min(bboxes1[:, 2:],bboxes2[:, 2:])
inter_min_xy = torch.max(bboxes1[:, :2],bboxes2[:, :2])
out_max_xy = torch.max(bboxes1[:, 2:],bboxes2[:, 2:])
out_min_xy = torch.min(bboxes1[:, :2],bboxes2[:, :2])
inter = torch.clamp((inter_max_xy - inter_min_xy), min=0)
inter_area = inter[:, 0] * inter[:, 1]
inter_diag = (center_x2 - center_x1)**2 + (center_y2 - center_y1)**2
outer = torch.clamp((out_max_xy - out_min_xy), min=0)
outer_diag = (outer[:, 0] ** 2) + (outer[:, 1] ** 2)
union = area1+area2-inter_area
dious = inter_area / union - (inter_diag) / outer_diag
dious = torch.clamp(dious,min=-1.0,max = 1.0)
if exchange:
dious = dious.T
return dious
(参考 DIoU 代码实现 https://blog.csdn.net/TJMtaotao/article/details/103317267)
3.4 CIoU Loss
在作者讲述 DIoU Loss 之后又在论文中引出了 CIoU Loss。作者的出发点是说,一个好的回归定位损失应该考虑三个几何参数:重叠面积 (IoU)、中心点距离 (d, c)、长宽比 ($\alpha, v$)。最终 CIoU 及其 Loss 计算公式如下所示:

注:上面表格最后一行看 (D) 的含义是将评价指标更换为 DIoU。
此博客 谈到,CIoU loss 的梯度类似于 DIoU loss,但还要考虑 $v$ 的梯度。在长宽在 [0, 1] 的情况下,$w^2 + h^2$ 的值通常很小,会导致梯度爆炸,因此在 $\frac{1}{w^2 + h^2}$ 实现时将替换成1。
def bbox_overlaps_ciou(bboxes1, bboxes2):
rows = bboxes1.shape[0]
cols = bboxes2.shape[0]
cious = torch.zeros((rows, cols))
if rows * cols == 0:
return cious
exchange = False
if bboxes1.shape[0] > bboxes2.shape[0]:
bboxes1, bboxes2 = bboxes2, bboxes1
cious = torch.zeros((cols, rows))
exchange = True
w1 = bboxes1[:, 2] - bboxes1[:, 0]
h1 = bboxes1[:, 3] - bboxes1[:, 1]
w2 = bboxes2[:, 2] - bboxes2[:, 0]
h2 = bboxes2[:, 3] - bboxes2[:, 1]
area1 = w1 * h1
area2 = w2 * h2
center_x1 = (bboxes1[:, 2] + bboxes1[:, 0]) / 2
center_y1 = (bboxes1[:, 3] + bboxes1[:, 1]) / 2
center_x2 = (bboxes2[:, 2] + bboxes2[:, 0]) / 2
center_y2 = (bboxes2[:, 3] + bboxes2[:, 1]) / 2
inter_max_xy = torch.min(bboxes1[:, 2:],bboxes2[:, 2:])
inter_min_xy = torch.max(bboxes1[:, :2],bboxes2[:, :2])
out_max_xy = torch.max(bboxes1[:, 2:],bboxes2[:, 2:])
out_min_xy = torch.min(bboxes1[:, :2],bboxes2[:, :2])
inter = torch.clamp((inter_max_xy - inter_min_xy), min=0)
inter_area = inter[:, 0] * inter[:, 1]
inter_diag = (center_x2 - center_x1)**2 + (center_y2 - center_y1)**2
outer = torch.clamp((out_max_xy - out_min_xy), min=0)
outer_diag = (outer[:, 0] ** 2) + (outer[:, 1] ** 2)
union = area1+area2-inter_area
u = (inter_diag) / outer_diag
iou = inter_area / union
with torch.no_grad():
arctan = torch.atan(w2 / h2) - torch.atan(w1 / h1)
v = (4 / (math.pi ** 2)) * torch.pow((torch.atan(w2 / h2) - torch.atan(w1 / h1)), 2)
S = 1 - iou
alpha = v / (S + v)
w_temp = 2 * w1
ar = (8 / (math.pi ** 2)) * arctan * ((w1 - w_temp) * h1)
cious = iou - (u + alpha * ar)
cious = torch.clamp(cious,min=-1.0,max = 1.0)
if exchange:
cious = cious.T
return cious
(参考 CIoU 代码实现 https://blog.csdn.net/TJMtaotao/article/details/103317267)
4. Focal Loss
Focal Loss 在网上争议比较大,有人说有用,有人说没有用。YOLOv3 原论文作者也有尝试使用 Focal Loss 性能还下降了两个点,作者也比较好奇。

Focal Loss 的讲解可参考我之前的博客 RetinaNet网络结构详解。
Focal Loss 很容易受到噪声影响,所以标注数据不要有错啊!!!
