深度学习之目标检测（五）-- RetinaNet网络结构详解

木卯 于 2021-08-17 发布

深度学习之目标检测（五）RetinaNet网络结构详解

本章学习 RetinaNet 相关知识，学习视频源于 Bilibili，部分参考叙述源自 知乎 。

img0

1. RetinaNet

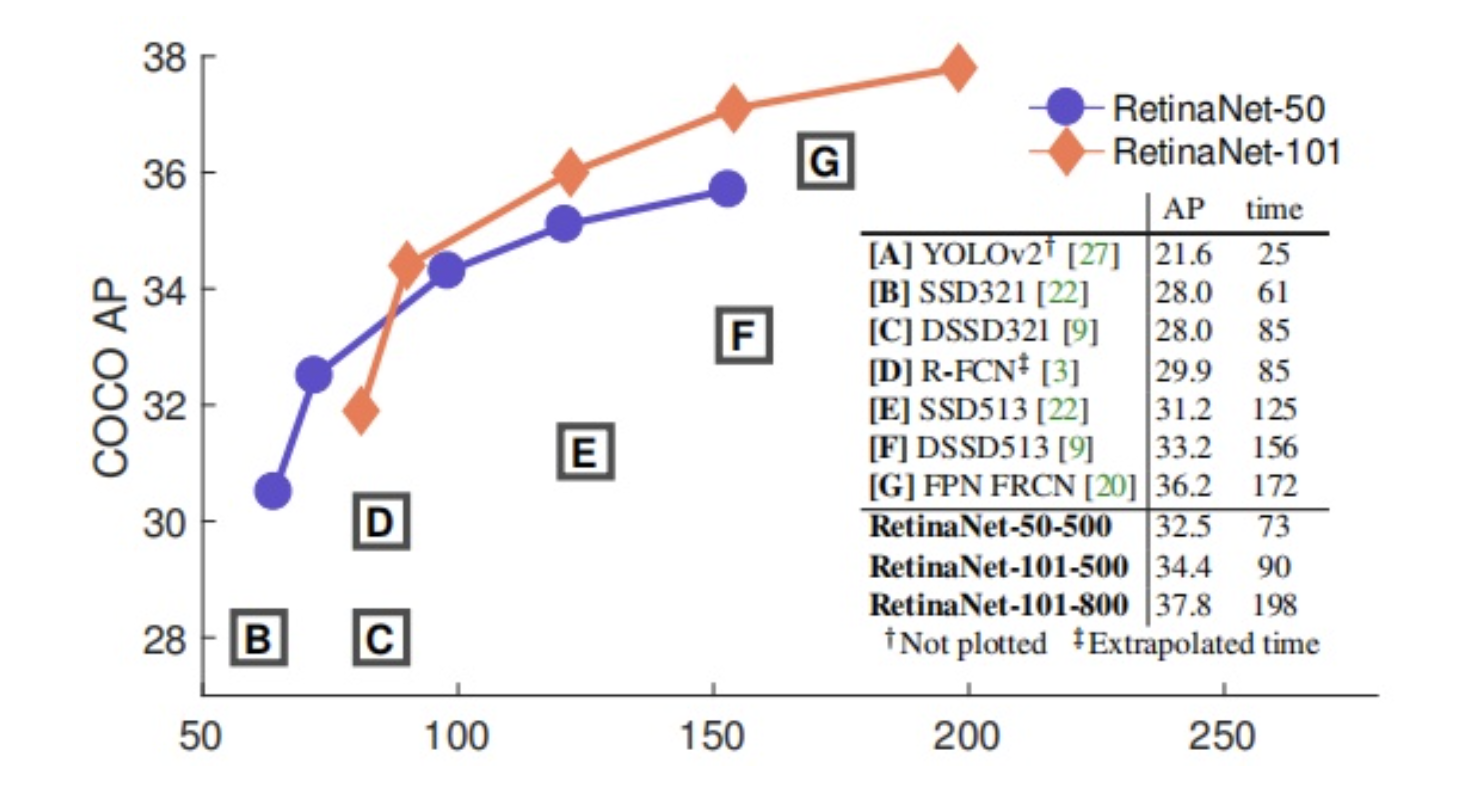
RetinaNet 原始论文为发表于 2017 ICCV 的 Focal Loss for Dense Object Detection。one-stage 网络首次超越 two-stage 网络，拿下了 best student paper，仅管其在网络结构部分并没有颠覆性贡献。

img1

img2

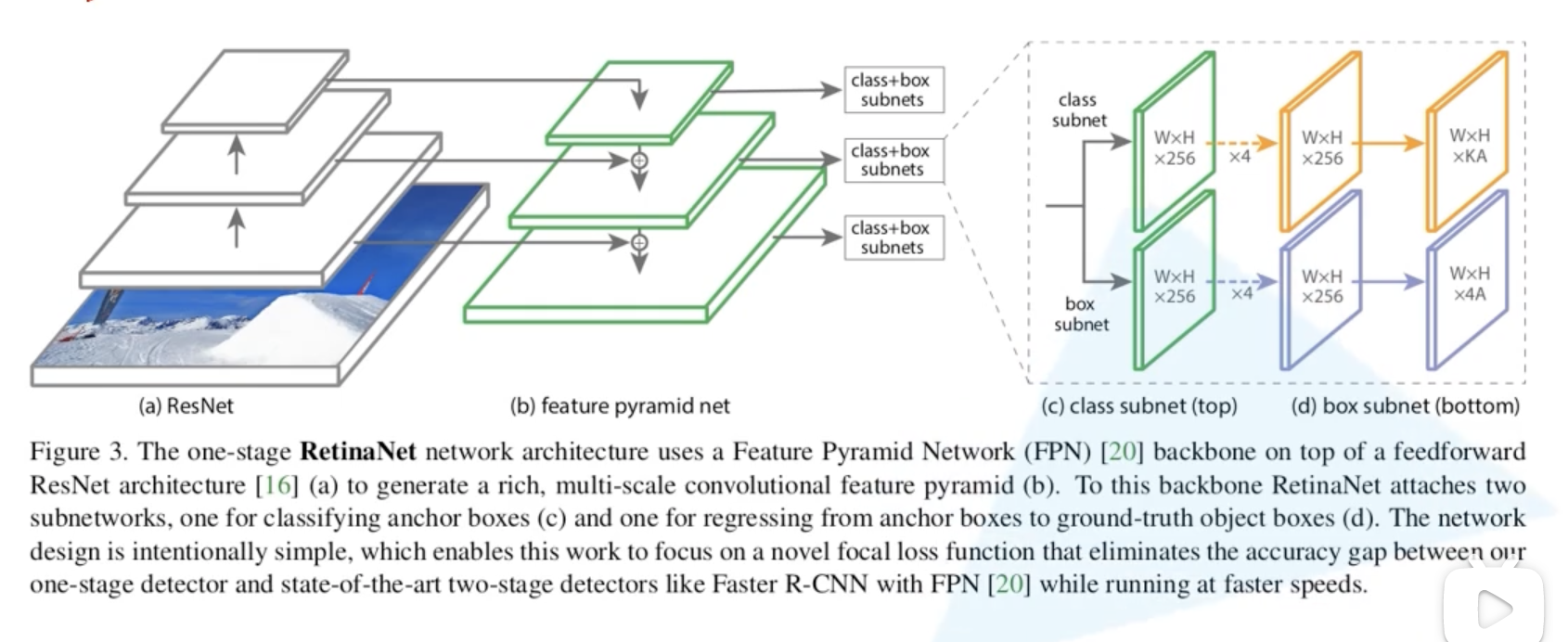
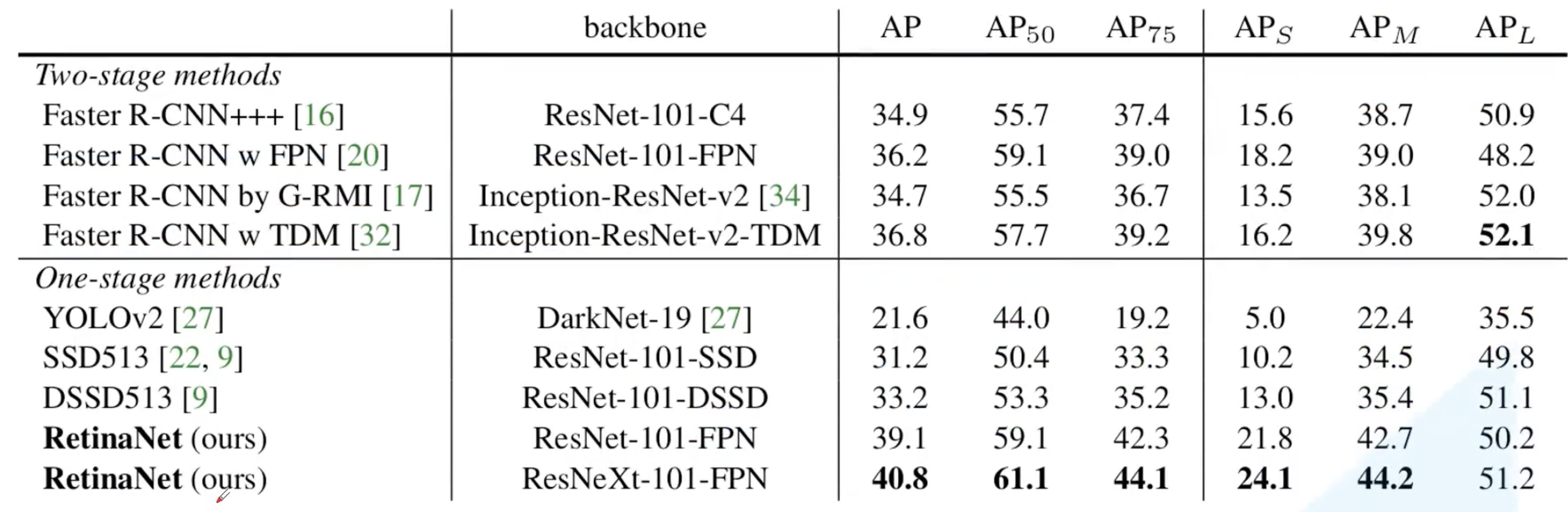
1.1 backbone 部分

RetinaNet 网络详细结构如下所示，与 FPN 不同，FPN 会使用 C2，而 RetinaNet 则没有，因为 C2 生成的 P2 会占用更多的计算资源，所以作者直接从 C3 开始生产 P3。关于 backbone 部分和 FPN 部分基本类似，所以具体细节部分就不细讲了。第二个不同点在于 P6 这个地方，原论文是在 C5 的基础上生成的（最大池化下采样得到的），这里是根据 pytorch 官方的实现绘制的，是通过 $3 \times 3$ 的卷积层来实现下采样的。第三个不同是 FPN 是从 P2 到 P6，而 RetinaNet 是从 P3 到 P7。

img3

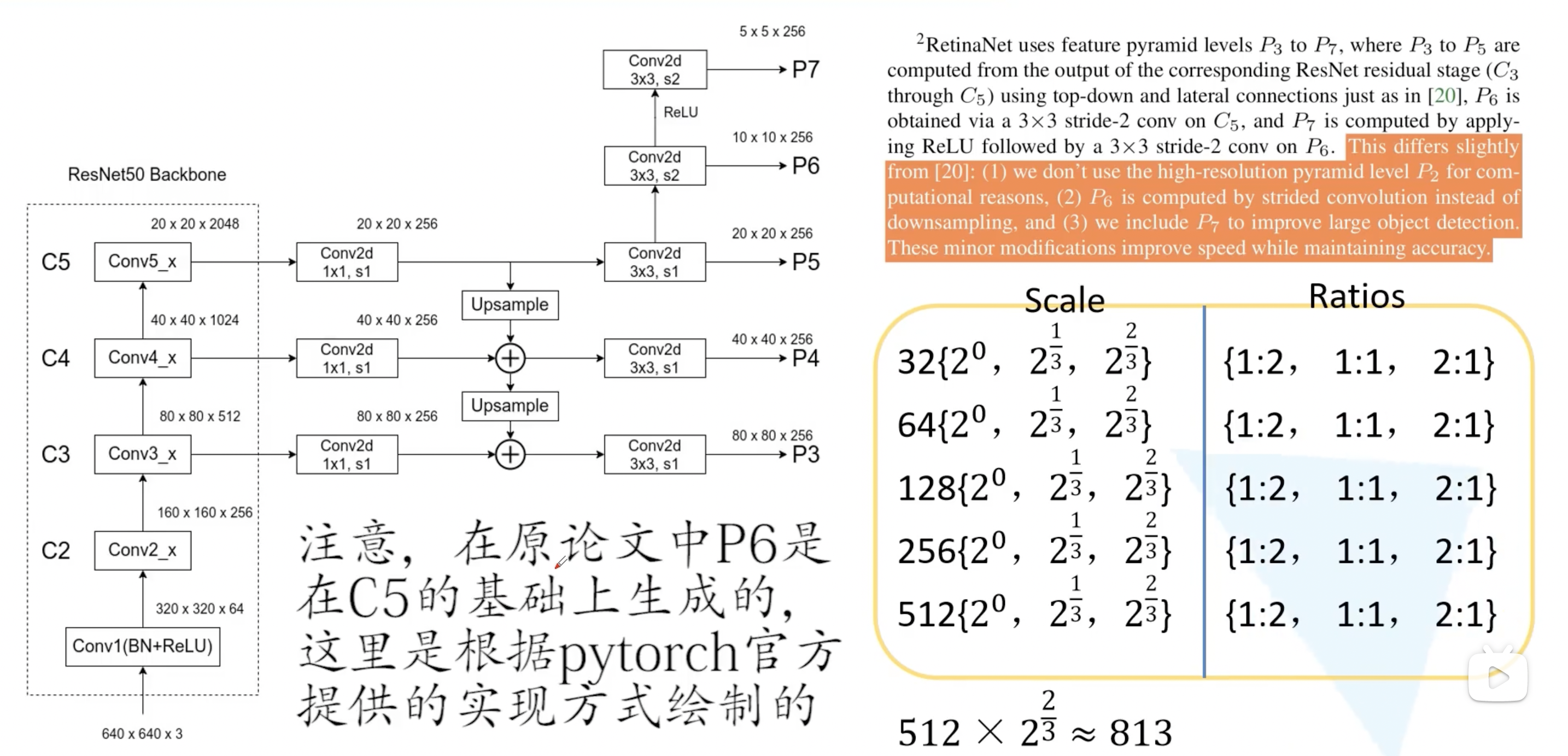
上图也给出了 P3 到 P7 上使用的 scale 和 ratios。在 FPN 中每个特征层上使用了一个 scale 和三个 ratios。在 RetinaNet 中是三个 scale 和三个 ratios 共计 9 个 anchor。 注意，这里 scale 等于 32 对应的 anchor 的面积是 32 的平方的。所以在 RetinaNet 中最小的 scale 是 32，最大的则是接近 813。

1.2 预测器部分

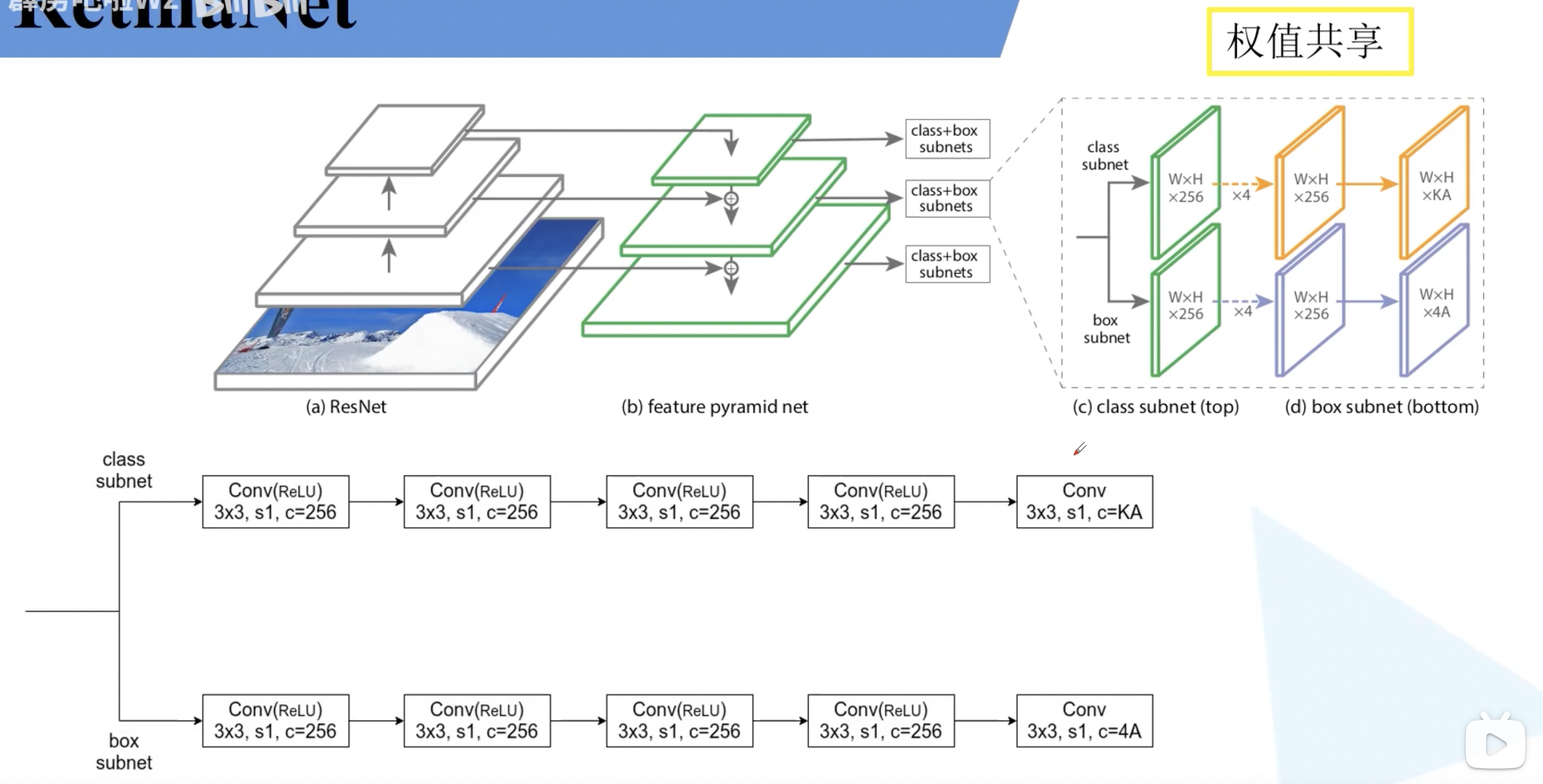
由于 RetinaNet 是一个 one-stage 的网络，所以不用 ROI pooling，直接使用如下图所示的权重共享的基于卷积操作的预测器。预测器分为两个分支，分别预测每个 anchor 所属的类别，以及目标边界框回归参数。最后的 kA 中 k 是检测目标的类别个数，注意这里的 k 不包含背景类别，对于 PASCAL VOC 数据集的话就是 20。这里的 A 是预测特征层在每一个位置生成的 anchor 的个数，在这里就是 9。（现在基本都是这样的类别不可知 anchor 回归参数预测，也可以理解为每一类共享了同一个 anchor 回归参数预测器）

img4

1.3 正负样本匹配

针对每一个 anchor 与事先标注好的 GT box 进行比对，如果 iou 大于 0.5 则是正样本，如果某个 anchor 与所有的 GT box 的 iou 值都小于 0.4，则是负样本。其余的进行舍弃。

img5

1.4 损失计算

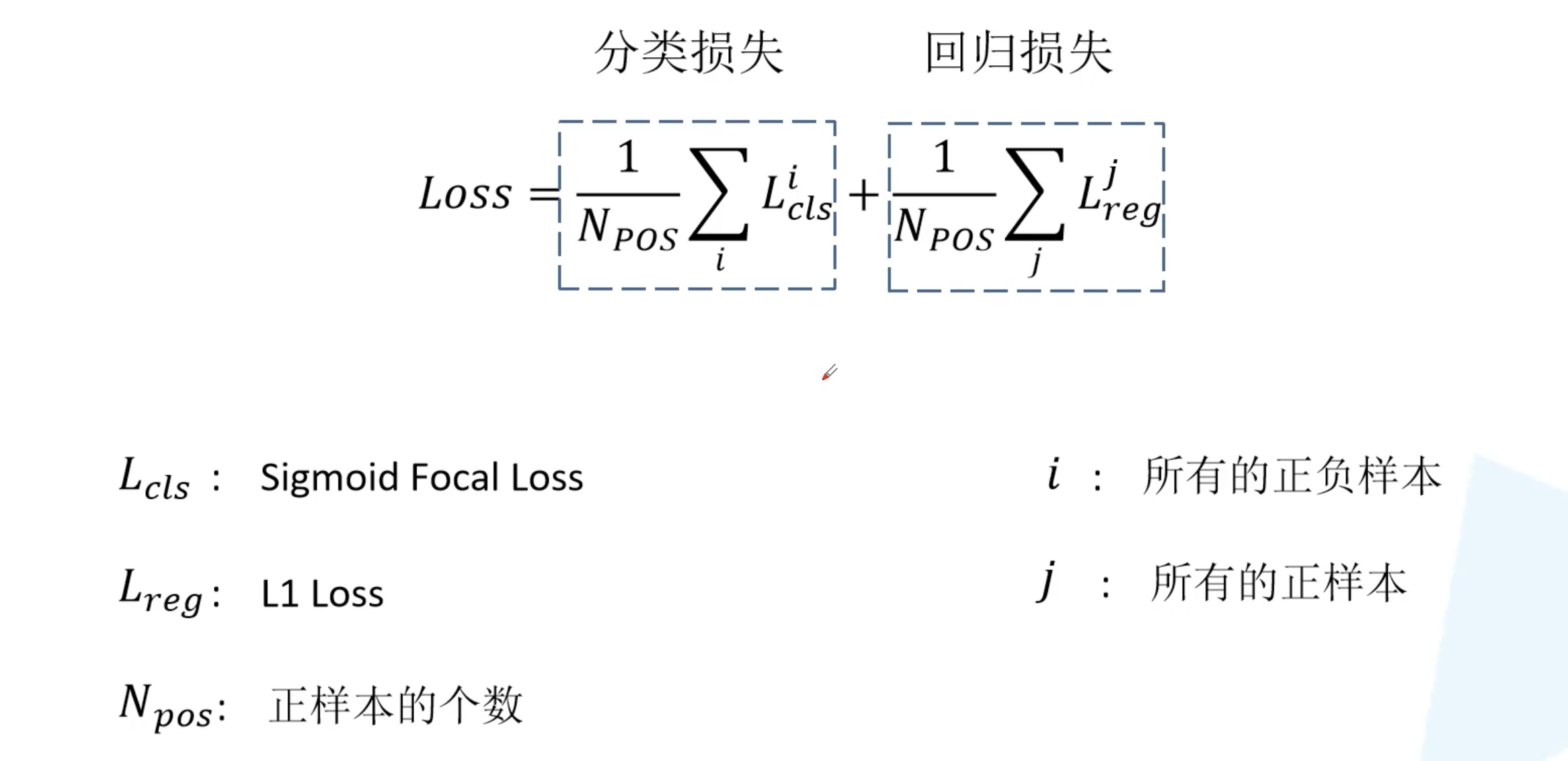
本文一个核心的贡献点就是 focal loss。总损失依然分为两部分，一部分是分类损失，一部分是回归损失。Focal loss 比较独特的一个点就是正负样本都会来计算分类损失，然后仅对正样本进行回归损失的计算。回归损失在 SSD 以及 Faster R-CNN 中都有讲解，这里就不细说了。

img6

2. Focal Loss

为了实现正负样本的比例均衡，不至于整个训练过程被负样本“淹没”，一般采取抽样的方法，将正负样本比例控制在1:3，从而在正负样本间保持合理的比例。因为 one-stage 只有一个阶段，产生的候选框相比 two-stage 要多太多。通常需要大约100K个位置（例如 SSD 的 8700+ 个位置），且这里面正样本几个十几个，少之又少。即使你抽样了，最后在训练过程中，还是会惊奇的发现，整个过程还是被大量容易区分的负样本，也就是背景所主导。Focal loss 则是一个动态缩放的交叉熵损失，一言以蔽之，通过一个动态缩放因子，可以动态降低训练过程中易区分样本的权重，从而将 loss 的重心快速聚焦在那些难区分的样本上 (注意：难以区分的样本不一定是正样本)。

img7

2.1 Cross Entropy Loss

Focal loss的起源是二分类交叉熵 CE，它的形式是这样的：

img8

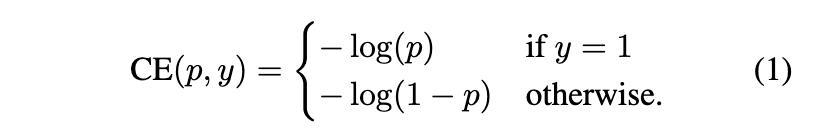
在上式中，$y$ 的取值有 1 和 -1 两种，代表前景和背景。$p$ 的取值范围是 [0,1]，是模型预测的属于前景的概率，为了表示方便，定义一个 $P_t$，如下所示：

img9

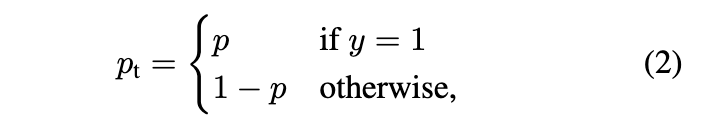
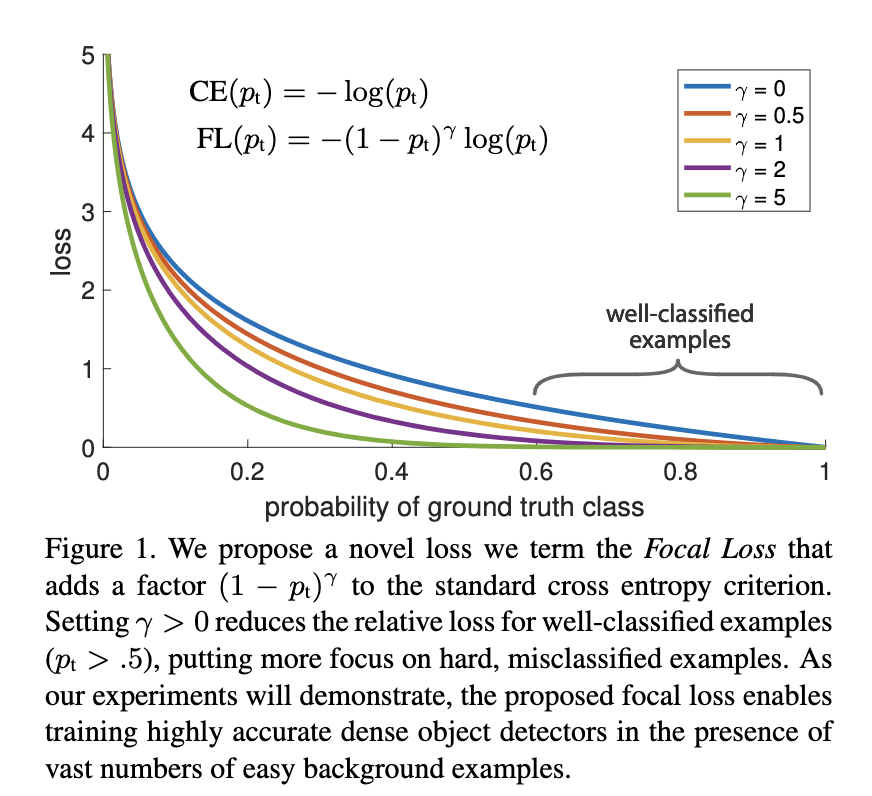
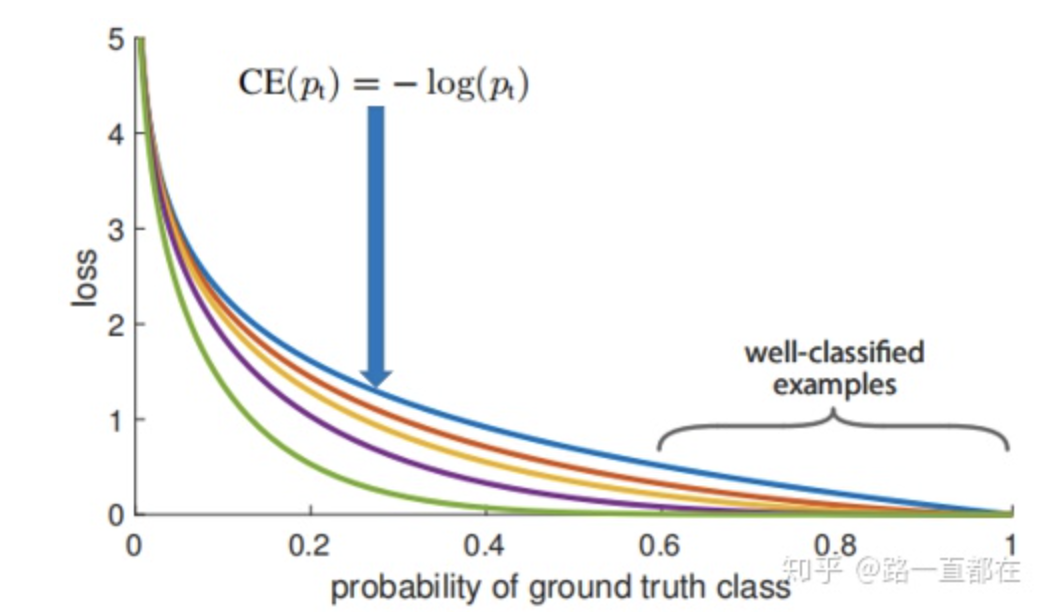
综合(1)(2)两个式子就可以得到： \(CE(p,y) = CE(p_t) = −\log(p_t).\) CE 曲线就是下图中的蓝色曲线，可以看到，相比较其他曲线，蓝色线条是变化最平缓的，即使在 $p>0.5$ (已经属于很好区分的样本)的情况下，它的损失相对于其他曲线仍然是高的，尽管它相对于自己前面的已经下降很多了，但是当数量巨大的易区分样本损失相加，就会主导我们的训练过程，所以要进一步增加前后损失的大小比。

img10

2.2 Balanced Cross Entropy

Balanced Cross Entropy 是常见的解决类不平衡的方法，其思想是引入一个权重因子 $\alpha \in [0,1]$，当类标签是 1 时，权重因子是 $\alpha$ ，当类标签是 -1 时，权重因子是 $1-\alpha$ 。同样为了表示方便，用 $\alpha_t$ 表示权重因子，那么此时的损失函数被改写为： \(CE(p,y) = −\alpha_t\log(p_t).\)

2.3 Focal Loss

Balanced Cross Entropy 解决了正负样本的比例失衡问题（positive/negative examples），但是这种方法仅仅解决了正负样本之间的平衡问题，并没有区分简单还是难分样本（easy/hard examples）。当容易区分的负样本的泛滥时，整个训练过程都是围绕容易区分的样本进行（小损失积少成多超过大损失），而被忽略的难区分的样本才是训练的重点。作者新引入了一个调制因子，公式如下： \(FL(p_t) = −(1-p_t)^{\gamma}\log(p_t).\) 其中 $\gamma$ 也是一个参数，范围在 [0,5]。观察上式可以发现，当 $P_t$ 趋向于 1 时，说明该样本比较容易区分，整个调制因子 $(1-p_t)^{\gamma}$ 是趋向于 0 的，也就是 loss 的贡献值会很小；如果某样本被错分，$p_t$ 很小，那么此时调制因子 $(1-p_t)^{\gamma}$ 是趋向 1 的，对 loss 没有大的影响（相对于基础的交叉熵），参数 $\gamma$ 能够调整权重衰减的速率。从下面这张图可以看出，当 $\gamma = 0$ 的时候，FL 就是原来的交叉熵损失 CE，随着 $\gamma$ 的增大，调整速率也在变化，实验表明，在 $\gamma =2$ 时，效果最佳。

img11

结合正负样本平衡以及难易样本平衡，最终的 Focal loss 形式如下： \(FL(p_t) = −\alpha_t(1-p_t)^{\gamma}\log(p_t).\) 它的功能可以解释为：通过 $α_t$ 可以抑制正负样本的数量失衡，通过 $\gamma$ 可以控制简单/难区分样本数量失衡。

对于 Focal loss，总结如下：