光流估计(一)仿射变换
由于过去做的研究是传统计算机视觉的图像梯度算法,所以近期想要了解一下光流估计的传统的“基于梯度的”算法。看似图像仿射变换和光流估计一点关系也没有,但是之后部分建模可能会用到它,所以先列在这。
仿射变换是在几何上定义为两个向量空间之间的一个仿射变换或者仿射映射(来自拉丁语,affine,“和…相关”)由一个非奇异的线性变换(运用一次函数进行的变换) 接上一个平移变换组成。对于图像的仿射变换而言,通常有 六 个参数。为什么是 6 个?
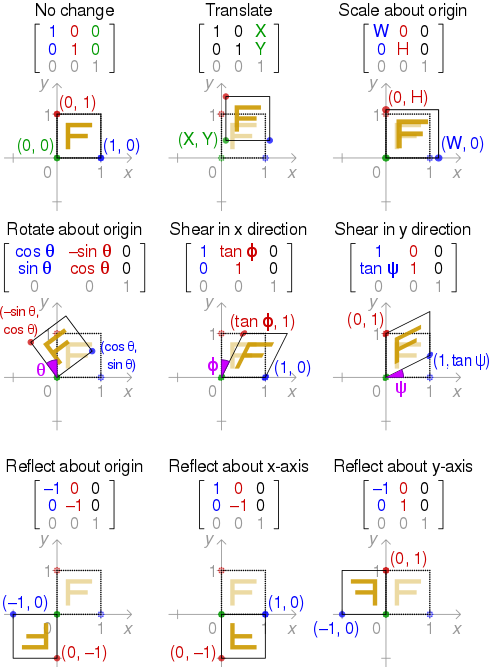
1. 仿射变换的一般定义
仿射变换为两函数的复合:平移 及 线性映射。普通向量代数用矩阵乘法呈现线性映射,用向量加法表示平移。一个对向量 $\vec{x}$ 平移 $\vec{b}$,与旋转放大缩小 $A$ 的仿射映射为:
\(\vec{y}=A \vec{x}+\vec{b}\) 上式在齐次坐标上(为了写成矩阵乘法形式,就和神经网络中把 bias 视作一个对应权重为 1 的输入神经元一样),等价于下式:
\(\left[\begin{array}{c} \vec{y} \\ 1 \end{array}\right]=\left[\begin{array}{cc} A & \vec{b} \\ 0, \ldots, 0 & 1 \end{array}\right]\left[\begin{array}{l} \vec{x} \\ 1 \end{array}\right]\) 这其实是一个 增广矩阵 与 增广向量 的乘积。
一仿射变换为可逆的当且仅当A为可逆的。在矩阵表示中,其逆元为:
\[\left[\begin{array}{cc} A^{-1} & -A^{-1} \vec{b} \\ 0, \ldots, 0 & 1 \end{array}\right] \\ \vec{y}=A \vec{x}+\vec{b} \Rightarrow \vec{x}=A^{-1}\vec{y}-A^{-1}\vec{b}\]2. 图像仿射变换 - 6个参数
图像二维仿射变换包括对二维影像的平移、旋转、放缩和拉伸,对应的二维仿射变换矩阵由 6 参数 ($a,b,c,d,e,f$) 组成。$(x,y)$ 表示原始影像的像素位置,$(X,Y)$ 表示变换后的像素位置,则 $X=ax+by+c, Y=dx+ey+f$。
先了解一下基础的变换有哪些:
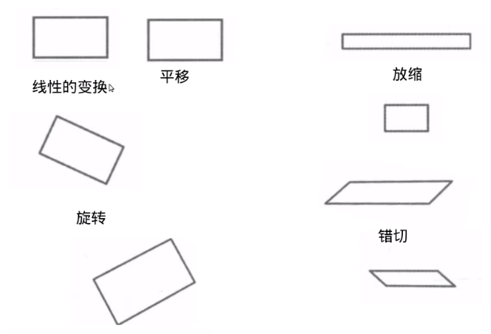
2.1 平移
对每一个像素点坐标平移。可以让每一个像素点的 x,y 坐标都加一个变量。矩阵形式表示为:
\(\left[\begin{array}{ccc} 1 & 0 & T_{x} \\ 0 & 1 & T_{y} \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{l} X \\ Y \\ 1 \end{array}\right]=\left[\begin{array}{c} X+T_{x} \\ Y+T_{y} \\ 1 \end{array}\right]\) 等式左边 $[X,Y,1]$ 是像素坐标的齐次形式。等式右边是平移之后的坐标的齐次形式。
2.2 放缩
进行放缩,就是将矩形(图像)放缩 $n$ 倍,也就是长宽各乘一个放缩系数变量:
\(\left[\begin{array}{ccc} W & 0 & 0 \\ 0 & H & 0 \\ 0 & 0 & 1 \end{array}\right] \left[\begin{array}{l} \mathbf{X} \\ \mathbf{Y} \\ 1 \end{array}\right]=\left[\begin{array}{c} W \mathbf{X} \\ H \mathbf{Y} \\ 1 \end{array}\right]\) 这里说一下,反射矩阵为:
\[\left[\begin{array}{ccc} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right] \quad \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{array}\right]\]2.3 旋转
对矩形(图片)进行旋转,也就是乘上一个旋转矩阵:
\[\left[\begin{array}{ccc} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{c} X_{0} \\ Y_{0} \\ 1 \end{array}\right]=\left[\begin{array}{c} X_{1} \\ Y_{1} \\ 1 \end{array}\right]\]2.4 错切
相比于前两个而言,错切没有那么直观,我们可以先从简单的形式入手。我们可以看下矩形关于 $y$ 方向的错切:
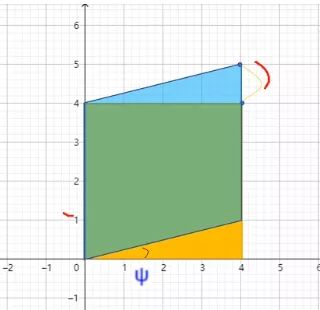
看图就很直观了,其对应的数学表达为:
\[\left[\begin{array}{ccc} 1 & 0 & 0 \\ \tan \Psi & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{c} X \\ Y \\ 1 \end{array}\right]=\left[\begin{array}{l} X \\ Y + X\tan \Psi \\ 1 \end{array}\right]\]$x$ 轴上的错切就是同理了,公式如下:
\(\left[\begin{array}{ccc} 1 & \tan \Phi & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{c} X \\ Y \\ 1 \end{array}\right]=\left[\begin{array}{l} X + Y\tan \Phi\\ Y \\ 1 \end{array}\right]\) 然后两者和起来,错切就如下了:
\[\left[\begin{array}{ccc} 1 & \tan \Phi & 0 \\ \tan \Psi & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{c} X \\ Y \\ 1 \end{array}\right]=\left[\begin{array}{l} X + Y\tan \Phi\\ Y + X\tan \Psi \\ 1 \end{array}\right]\]到此我们就了解了这四种变换了,那仿射变换是什么呢?可以看下图公式 (最后的平移是为了把图片移动回第一象限,因为图像坐标都是正数):
\[\begin{array}{l} {\left[\begin{array}{ccc} 1 & 0 & T_x \\ 0 & 1 & T_y \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{ccc} \cos \Theta & -\sin \Theta & 0 \\ \sin \Theta & \cos \Theta & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{ccc} W & 0 & 0 \\ 0 & H & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{ccc} 1 & \tan \phi & 0 \\ \tan \psi & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{ccc} 1 & 0 & T^{\prime}_x \\ 0 & 1 & T^{\prime}_y \\ 0 & 0 & 1 \end{array}\right]=\left[\begin{array}{ccc} a_{0} & a_{1} & b_{1} \\ a_{2} & a_{3} & b_{2} \\ 0 & 0 & 1 \end{array}\right]} \end{array}\]等式右边就是仿射变换矩阵,是由原图像旋转,放缩,错切,平移之后得来的。这得到的,就是题所说的六个参数。这六个参数之间是没有什么公式关系的,但各个参数却也不是简单的代表了某个变换,而都是各个变换叠加而成的。
仿射变换中集合中的一些性质保持不变: (1)凸性 (2)共线性:若几个点变换前在一条线上,则仿射变换后仍然在一条线上 (3)平行性:若两条线变换前平行,则变换后仍然平行 (4)共线比例不变性:变换前一条线上两条线段的比例,在变换后比例仍然不变
注:所有的三角形都能通过仿射变化为其他三角形,所有平行四边形也能仿射变换为另一个平行四边形
注:透视变换和放射变换不同,透视变换可以变换平行四边形成任意不规则四边形。
