深度学习之图像分类(三十)Hire-MLP网络详解
一晃都学习了三十个网络了,时间过得真快。本次学习华为提出的 Hire-MLP,依然是通过旋转特征图,将不同位置的特征对齐到同一个通道上从而实现 MLP-based Model 中的局部感受野依赖。

1. 前言
本此学习华为诺亚&北大&悉尼大学联合提出的 HireMLP。关于 MLP-Mixer 的两大主要问题我们已经在前面的学习中阐述了很多遍:对于 Token 进行全局感受野卷积,容易过拟合且对图像尺寸敏感,无法作为 Backbone 用于下游任务。Hire-MLP 也提出:如何在 MLP-based 模型中结合局部感受野和全局感受野,同时对图像输入分辨率不敏感是值得探索的地方。为了对输入图像尺寸不敏感,要不使用固定尺寸小卷积核(例如 $3 \times 3$ 的DW Conv);或者就是移动特征图,使得不同 token 对齐到同一个通道上,然后使用 $1 \times 1$ 卷积来实现局部感受野,即不同 token 之间的信息融合。Hire-MLP 也是一样的思路,通过移动特征图(本工作称之为区域重排 Region Rearrangement),从而实现局部信息的整合。本工作的原始论文为 Hire-MLP: Vision MLP via Hierarchical Rearrangement。2021.8.30 挂上 arXiv,代码并未开源。最终在 ImageNet 上达到了 83.4% 的 Top-1 精度,这与 SOTA 的 Swin Transformer 等相当。虽然 Hire-MLP 结构上对下游任务友好,但是本文并没有将其应用于下游任务,从而不清楚其真实性能。
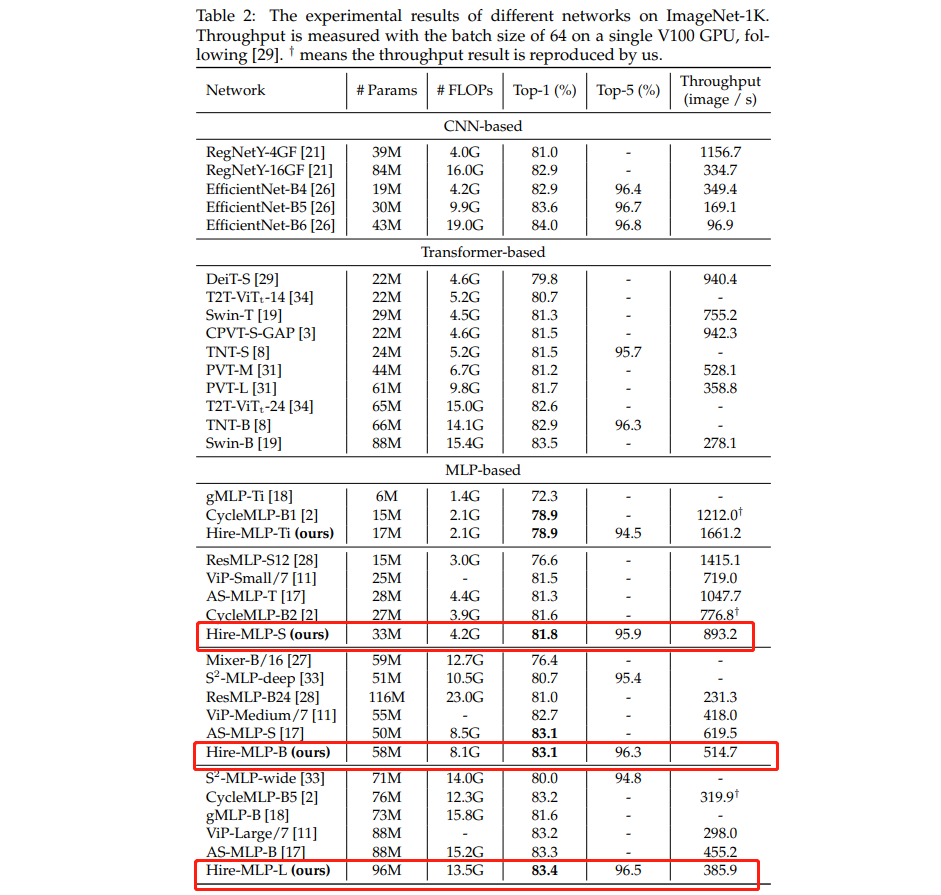
从结果可见:
- Hire-MLP-S 取得了 81.8% 的精度,而计算量仅为 4.2G Flops,优于其他 MLP 方案。相比 AS-MLP、CycleMLP,所提 Hire-MLP 性能更佳。
- Hire-MLP-B 与 Hire-MLP-L 分别取得了 83.1% 与 83.4% 的精度,而计算量分别为 8.1G 与 13.5G。
- 相比 DeiT、Swin 以及 PVT,所提方案具有更快的推理速度;
- 相比 RegNetY,所提方案具有更高的精度,同时具有相似的模型大小和复杂度。
- 相比AS-MLP,Hire-MLP好像并没有什么优势,性能相当,速度反而AS-MLP更快 。(AS-MLP 源代码的 Shift 操作是用 cupy 库自己编程实现的,可能会有影响)
2. Hire-MLP
这次讲解我先讲局部 Hire-MLP Block 结构,再描述网络的整体结构。
2.1 Hire-MLP Block
单个 Hire-MLP Block 依然是分为 Token-mixing MLP 和 Channel mixing MLP,其中作者主要的贡献点在于替换 MLP-mixer 的 Token-mixing MLP 为 Hire-Module。所以整个 Hire-MLP Block 可以描述为: \(\begin{aligned} &Y=\text { Hire-Module }(\operatorname{LN}(X))+X \\ &Z=\text { Channel-MLP }(\operatorname{LN}(Y))+Y \end{aligned}\) Channel MLP 就是最普通的两层全连接,中间使用 GELU 激活函数,第一层全连接结点个数一般为输入结点个数的 2,3 或者 4 倍。或者可以直接称之为通道方向的 $1 \times 1$ 卷积。
Hire-Module 的内部结构如下图所示,其中包含三条支路,分别是对于 H 方向的重排,W 方向的重排,以及通道方向的映射:
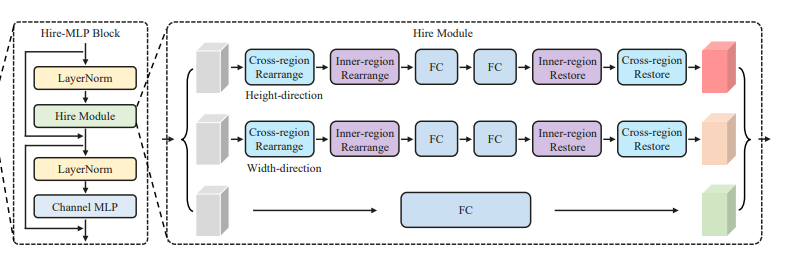
重排分为两类:Cross-Region 以及 Inner-Region。
2.1.1 Inner-Region
Height-direction 的 Inner-Region 其实就是对特征图进行 H 维度的分组,然后将其切分开之后堆叠到通道维度。这里 $H$ 为原始特征图的高度,$h$ 为每一小组内特征图的高度。即对于一个 $H \times W \times C$ 的特征图可以分成 $g = H / h$ 组,每组的特征图大小为 $h \times W \times C$,然后对特征图进行重排得到 $g \times W \times (hC)$,此后做 $hC->hC$ 的映射。映射结束后,再还原到 $H \times W \times C$ 的特征图即可。可视化流程如下所示:
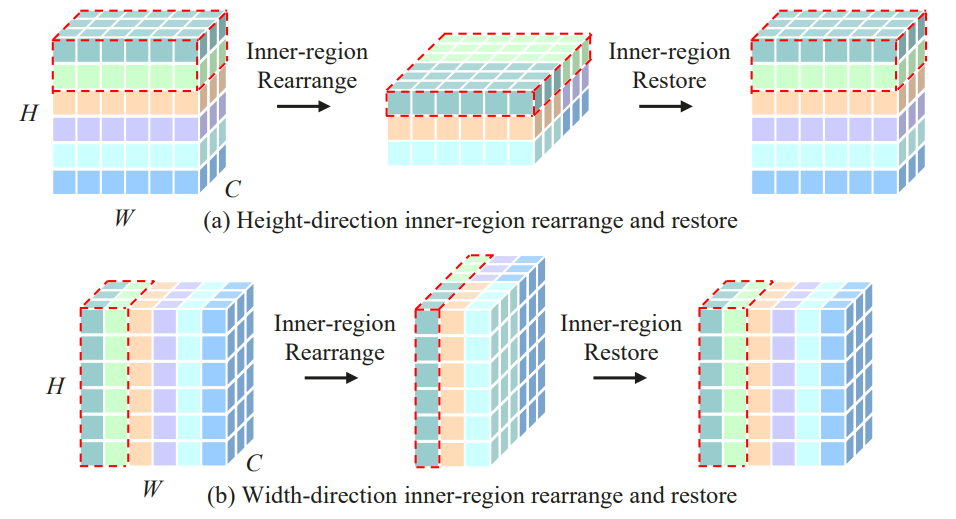
具体的映射其实是依赖两个全连接和一个 GELU 激活函数构成的,论文中作者将第一个全连接层的阶段设定为 $C / 2$ 用于降维和减少计算量。其实也可以只依赖两个 $1 \times 1$ 卷积加以实现。
Inner-Region 重排其实可以只需要依赖 einops 库的 Rearrange 即可方便完成:
import torch
from torch import nn
from einops.layers.torch import Rearrange, Reduce
class InnerRegionW(nn.Module):
def __init__(self, w):
super().__init__()
self.w = w
self.region = nn.Sequential(
Rearrange('b c h (w group) -> b (c w) h group', w = self.w) # 重排
)
def forward(self, x):
return self.region(x)
class InnerRegionRestoreW(nn.Module):
def __init__(self, w):
super().__init__()
self.w = w
self.region = nn.Sequential(
Rearrange('b (c w) h group -> b c h (w group)', w = self.w) # 恢复
)
def forward(self, x):
return self.region(x)
model1 = InnerRegionW(w = 2)
model2 = InnerRegionRestoreW(w = 2)
images = torch.randn(1, 1, 4, 4)
print(images)
print("==============================")
with torch.no_grad():
output1 = model1(images)
output2 = model2(output1)
print("=========== output1 ==============")
print(output1)
print("=========== output2 ==============")
print(output2)
2.1.2 Cross-Region
单个方向的 Inner-Region 产生的是特定的一维线性感受野,即将 $h \times w$ 拆分成 $1 \times w$ 和 $h \times 1$ 的形式,由于输入是 $224 \times 224$ 的方图,所以一般配置中 $h = w$。并且 Inner-Region 的空间位置相对固定,即和 Swin 分窗一样,窗口固定了,则窗口处理始终对应的都是固定的区域。为了使得不同窗内的 Token 有交互,需要移动窗,或者说需要旋转特征图。这就引发了 Cross-Region。请联系 Swin 一起思考,则容易理解多了。
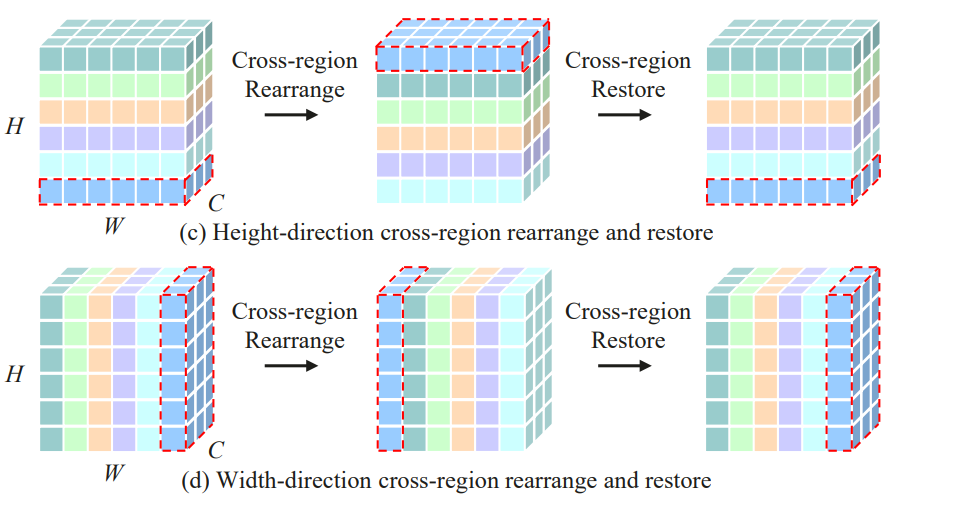
Height-direction 的 Inner-Region 其实就是对特征图进行 H 维度的转动,转动的步长设定为 $s$ ,通常 $s$ 取 1 或者 2。Cross-Region 操作被加在 Inner-Region 前后。实际上并不是每个 Inner-Region 前后都添加 Cross-Region,因为每一个都添加一样的 Cross-Region 其实等于没有添加。所以原文中作者是隔一个添加一个,隔一个添加一个。To get a global receptive field, the cross-region rearrangement operations are inserted before the inner-region rearrangement operation every two blocks. 但是作者将这个称为全局感受野我其实是不太认同的,毕竟 $s$ 太小了,只不过边界地区挨到一起来罢了,这其实也是局部感受野而已…
Cross-Region 重排其实可以只需要依赖 torch.roll 即可方便完成:
import torch
from torch import nn
from einops.layers.torch import Rearrange, Reduce
class CrossRegion(nn.Module):
def __init__(self, step = 1, dim = 1):
super().__init__()
self.step = step
self.dim = dim
def forward(self, x):
return torch.roll(x, self.step, self.dim)
model1 = CrossRegion(step = 2, dim = 3)
model2 = CrossRegion(step = -2, dim = 3)
model3 = CrossRegion(step = 1, dim = 2)
model4 = CrossRegion(step = -1, dim = 2)
images = torch.randn(1, 1, 5, 5)
print(images)
print("==============================")
with torch.no_grad():
output1 = model1(images)
output2 = model2(images)
output3 = model3(images)
output4 = model4(images)
print("=========== output1 ==============")
print(output1)
print("=========== output2 ==============")
print(output2)
print("=========== output3 ==============")
print(output3)
print("=========== output4 ==============")
print(output4)
2.1.3 特征融合
在 Hire-Module 中有三个并行的支路,第三条之路只需要通过一个 $C -> C$ 的单层全连接层映射。最后三条支路的特征图直接加和即可获得最终的融合特征图。其实用一下 Split-Attention 或者如 sMLPNet 说的通道拼接后经过 $1 \times 1$ 卷积降维可能还会涨点,不过计算量会有所增加。所以最终不难分析得到 Hire-Module 是一个十字形的感受野。整个 Hire-MLP Block 的推理逻辑如下所示:
def forward(self, x):
x_h = self.inner_regionH(self.cross_regionH(x)) # 重排
x_w = self.inner_regionW(self.cross_regionW(x)) # 重排
x_h = self.proj_h(x_h) # 映射
x_w = self.proj_w(x_w) # 映射
x_c = self.proj_c(x) # 映射
x_h = self.cross_region_restoreH(self.inner_region_restoreH(x_h)) # 恢复
x_w = self.cross_region_restoreW(self.inner_region_restoreW(x_w)) # 恢复
out = x_c + x_h + x_w # 特征融合
return out
2.1.4 HireMLP 和 ViP,AS-MLP 的区别?
HireMLP 和 ViP 有区别吗?在我看来没有本质区别,ViP 也是分组重排操作。ViP 更复杂地使用了 Split-Attention 和残差;HireMLP 则是将中间的映射改为两层全连接。HireMLP 作者说 Inspired by the shortcut in ResNet and ViP, an extra branch without spatial communication is alse added ...,但是看起来似乎不仅仅是像他们一样添加一个 extra branch without spatial communication 这么简单,而是整个模块其实思想都是惊人的一致。至于说指标报告方面 HireMLP 高了那么 0.2%,会不会是因为两层全连接导致的?尚不可而知。不过相比 ViP 的重排,能肉眼可见的改进就是这个地方了。
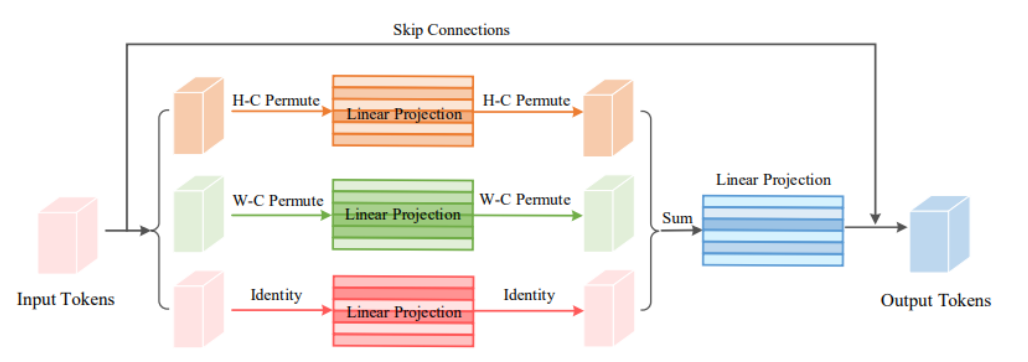
HireMLP 和 AS-MLP 有区别吗?在我看来没有本质区别,AS-MLP 也是十字形感受野,不过是位移的实现方式上有所不同。整体而言都是类似的。相比AS-MLP,Hire-MLP好像并没有什么优势,性能相当,速度反而AS-MLP更快。所以说:在特征图移动上玩花似乎已经走到头了,玩不出什么花来了。
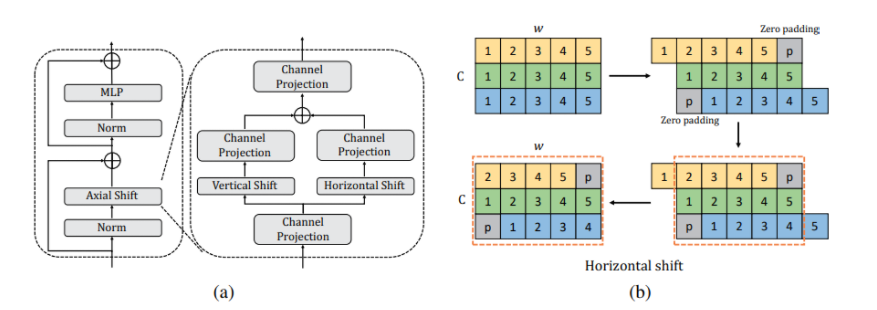
2.2 整体网络结构
Hire-MLP 的 Patch Embedding 很有特色,使用卷积核大小为 $7 \times 7$ ,步长为 4 的卷积。相比而言 Swin 使用卷积核大小为 $4 \times 4$,步长为 4 的卷积。在近期的我自己的小实验中也发现:Patch Embedding 时具有重叠会更好,这样可以避免边界效应并在小数据集上提升性能。Hire-MLP 中间采用多阶段金字塔模型,总共分为 4 个阶段,每个阶段交替重复使用 Hire-MLP Block。下采样使用卷积核大小为 $3 \times 3$,步长为 2 的卷积,这样做也有重叠。最后经过全局池化后连接一个全连接分类器即可,其网络结构图如下所示:
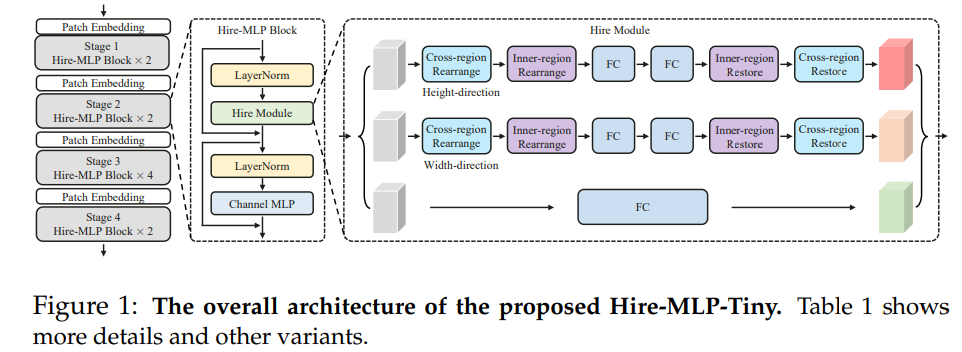
作者一共提出来了四种配置:
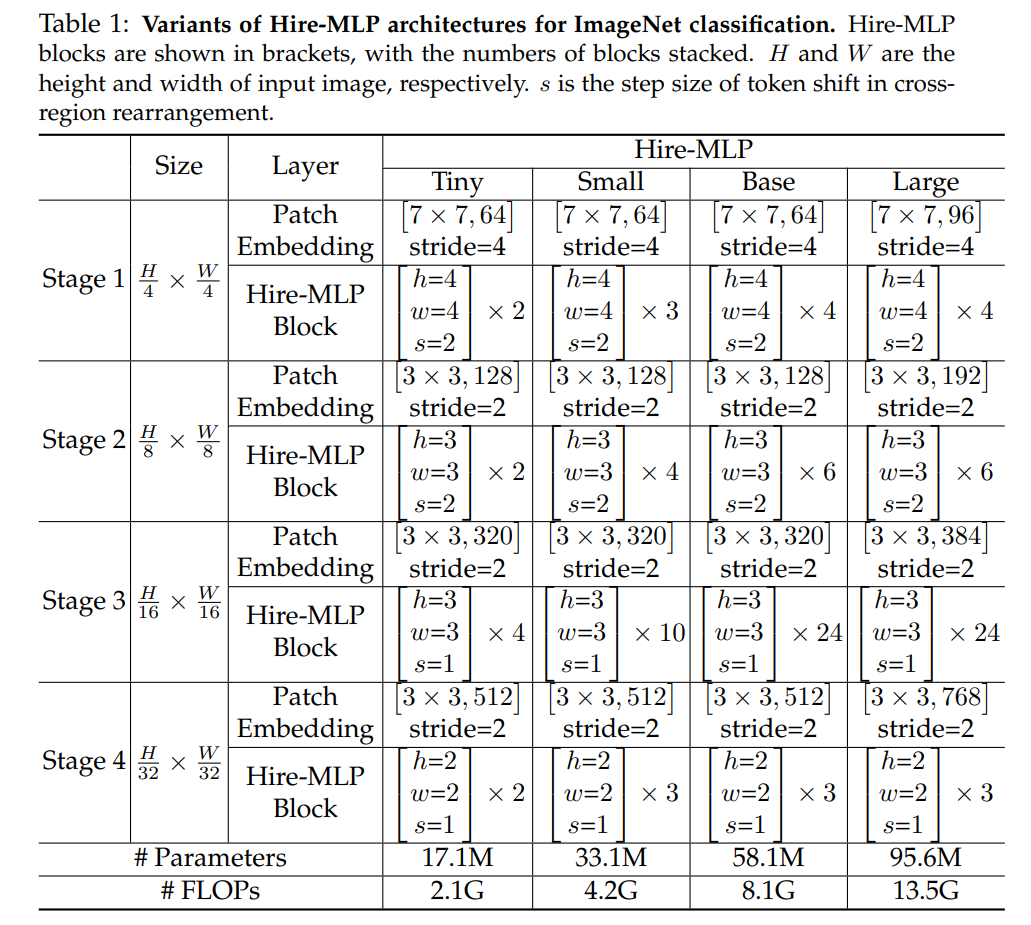
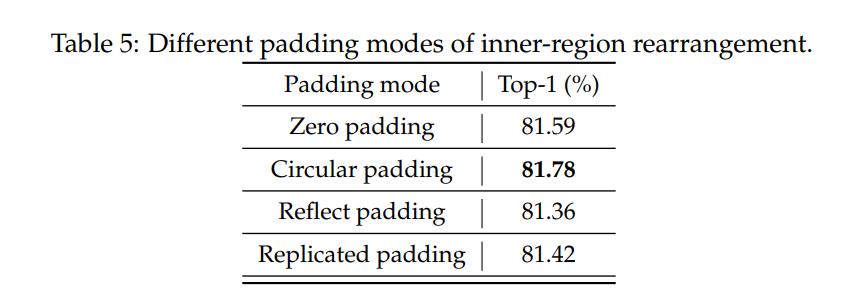
大家注意这四种配置,其中 Hire-MLP Block 中 $h,w,s$ 的取值一样的。$h,w$ 指 Inner-Region 中分小组内 H 或者 W 维度的大小,$s$ 指 Cross-Region 处旋转的步长。注意到 $H$ 不一定整除 $h$,让我们以 Base 为例,作者在训练 ImageNet 的时候以 $224 \times 224$ 的图片作为输入,经过第一个 Patch Embedding 之后,假设作者 kernel size = 7, stride = 4,假设使用了 padding = 3,则此后特征图大小为 $56 \times 56 \times 64$。此后在 Stage 1 中 $h = w = 4$,即在 Inner-Region 中可以分为 $56 / 4 = 14$ 组,特征图可以重排为 $14 \times 56 \times 256$,然后做 $256 -> 32 -> 256$ 的映射 ($hC -> C/2 -> hC$),看上去没什么问题。经过下采样的 Patch Embedding,kernel size = 3,stride = 2,假设使用了 padding = 1,则此后特征图大小为 $28 \times 28 \times 128$。这里 28 根本不是 3 的倍数,所以需要进行 padding 操作。作者通过对比发现 Circular padding 是最好的,但是 padding 类别其实对结果的影响并不大。
3. 消融实验
作者一共进行了多组消融实验:
- Inner-Region 中 $h, w$ 的影响:作者发现浅层使用大一点点的 $h,w$,深层使用小一点的 $h, w$ 效果更好,最终使用 $h = w = [4,3,3,2]$

- Cross-Region 中 $s$ 的影响:作者发现浅层使用大一点点的 $s$,深层使用小一点的 $s$ 效果更好,最终使用 $s = [2,2,1,1]$,所以其实 Cross-Region 并没有实现大感受野信息交换…

- 不同 padding 策略的影响:最终发现padding 类别其实对结果的影响并不大,Circular padding 效果略好。

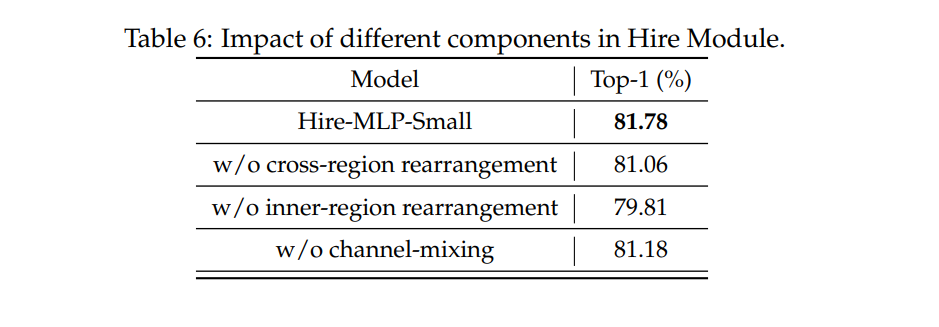
- Hire Module 中不同模块的作用效果:可见去除 Inner-Region 或者 Cross-Region 性能都会下降,其中 Inner-Region 有关局部感受野,去除了只剩下 Cross-Region 其实等价于朴素的只有通道方向的映射,所以性能影响更大。但是只有通道方向的映射,真的作者能做到 79.81% 吗?我持保留意见!
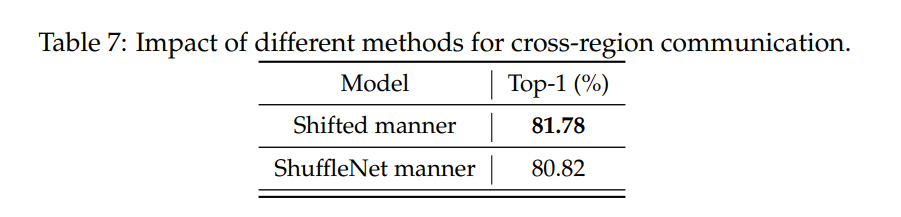
- Cross-Region 的 shift 方式:作者比较了直接旋转的 Shifted manner 与 ShuffleNet 那样的分组的方式,最终发现 Shifted manner 会更好,这也符合直觉,因为图像中随机膈几列选一列的做法其实局部性并不保证了。可见局部性还是比较重要的。但是真的性能只差一丝丝吗?
4. 总结与反思
Hire-MLP 其实依然是使用特征图移动,使得不同空间位置的 token 对齐到统一通道,然后使用通道方向的 $1 \times 1$ 卷积实现的局部依赖性引入和对图像分辨率不敏感,这种思想在过去的诸多工作例如 AS-MLP 以及 ViP,S2MLPv2 等中均可看到,所以并不是什么新鲜的贡献。此外作者说 Hire-MLP 对下游任务友好,但是并没有进行实验让人有点点失望。本工作暂未开源,所报告性能我持怀疑态度,因为作者消融实验中去除 Inner-Region 只保留 Cross-Region 其实可看作仅有 Channel 方向 $1 \times 1$ 卷积的网络,也能达到 79.81%?比 MLP-Mixer 的 76+% 还高?
5. 代码
我自己实现的非官方 pytorch 代码见 此处,欢迎与大家自己复现的进行交流。
import torch
from torch import nn
from functools import partial
from einops.layers.torch import Rearrange, Reduce
from .utils import pair
class PreNormResidual(nn.Module):
def __init__(self, dim, fn, norm = nn.LayerNorm):
super().__init__()
self.fn = fn
self.norm = norm(dim)
def forward(self, x):
return self.fn(self.norm(x)) + x
class PatchEmbedding(nn.Module):
def __init__(self, dim_in, dim_out, kernel_size, stride, padding, norm_layer=False):
super().__init__()
self.reduction = nn.Sequential(
nn.Conv2d(dim_in, dim_out, kernel_size=kernel_size, stride=stride, padding = padding),
nn.Identity() if (not norm_layer) else nn.Sequential(
Rearrange('b c h w -> b h w c'),
nn.LayerNorm(dim_out),
Rearrange('b h w c -> b c h w'),
)
)
def forward(self, x):
return self.reduction(x)
class FeedForward(nn.Module):
def __init__(self, dim_in, hidden_dim, dim_out):
super().__init__()
self.net = nn.Sequential(
nn.Conv2d(dim_in, hidden_dim, kernel_size = 1),
nn.GELU(),
nn.Conv2d(hidden_dim, dim_out, kernel_size = 1),
)
def forward(self, x):
return self.net(x)
class CrossRegion(nn.Module):
def __init__(self, step = 1, dim = 1):
super().__init__()
self.step = step
self.dim = dim
def forward(self, x):
return torch.roll(x, self.step, self.dim)
class InnerRegionW(nn.Module):
def __init__(self, w):
super().__init__()
self.w = w
self.region = nn.Sequential(
Rearrange('b c h (w group) -> b (c w) h group', w = self.w)
)
def forward(self, x):
return self.region(x)
class InnerRegionH(nn.Module):
def __init__(self, h):
super().__init__()
self.h = h
self.region = nn.Sequential(
Rearrange('b c (h group) w -> b (c h) group w', h = self.h)
)
def forward(self, x):
return self.region(x)
class InnerRegionRestoreW(nn.Module):
def __init__(self, w):
super().__init__()
self.w = w
self.region = nn.Sequential(
Rearrange('b (c w) h group -> b c h (w group)', w = self.w)
)
def forward(self, x):
return self.region(x)
class InnerRegionRestoreH(nn.Module):
def __init__(self, h):
super().__init__()
self.h = h
self.region = nn.Sequential(
Rearrange('b (c h) group w -> b c (h group) w', h = self.h)
)
def forward(self, x):
return self.region(x)
class HireMLPBlock(nn.Module):
def __init__(self, h, w, d_model, cross_region_step = 1, cross_region_id = 0, cross_region_interval = 2, padding_type = 'circular'):
super().__init__()
assert (padding_type in ['constant', 'reflect', 'replicate', 'circular'])
self.padding_type = padding_type
self.w = w
self.h = h
# cross region every cross_region_interval HireMLPBlock
self.cross_region = (cross_region_id % cross_region_interval == 0)
if self.cross_region:
self.cross_regionW = CrossRegion(step = cross_region_step, dim = 3)
self.cross_regionH = CrossRegion(step = cross_region_step, dim = 2)
self.cross_region_restoreW = CrossRegion(step = -cross_region_step, dim = 3)
self.cross_region_restoreH = CrossRegion(step = -cross_region_step, dim = 3)
else:
self.cross_regionW = nn.Identity()
self.cross_regionH = nn.Identity()
self.cross_region_restoreW = nn.Identity()
self.cross_region_restoreH = nn.Identity()
self.inner_regionW = InnerRegionW(w)
self.inner_regionH = InnerRegionH(h)
self.inner_region_restoreW = InnerRegionRestoreW(w)
self.inner_region_restoreH = InnerRegionRestoreH(h)
self.proj_h = FeedForward(h * d_model, d_model // 2, h * d_model)
self.proj_w = FeedForward(w * d_model, d_model // 2, w * d_model)
self.proj_c = nn.Conv2d(d_model, d_model, kernel_size = 1)
def forward(self, x):
x = x.permute(0, 3, 1, 2)
B, C, H, W = x.shape
padding_num_w = W % self.w
padding_num_h = H % self.h
x = nn.functional.pad(x, (0, self.w - padding_num_w, 0, self.h - padding_num_h), self.padding_type)
x_h = self.inner_regionH(self.cross_regionH(x))
x_w = self.inner_regionW(self.cross_regionW(x))
x_h = self.proj_h(x_h)
x_w = self.proj_w(x_w)
x_c = self.proj_c(x)
x_h = self.cross_region_restoreH(self.inner_region_restoreH(x_h))
x_w = self.cross_region_restoreW(self.inner_region_restoreW(x_w))
out = x_c + x_h + x_w
out = out[:,:,0:H,0:W]
out = out.permute(0, 2, 3, 1)
return out
class HireMLPStage(nn.Module):
def __init__(self, h, w, d_model_in, d_model_out, depth, cross_region_step, cross_region_interval, expansion_factor = 2, dropout = 0., pooling = False, padding_type = 'circular'):
super().__init__()
self.pooling = pooling
self.patch_merge = nn.Sequential(
Rearrange('b h w c -> b c h w'),
PatchEmbedding(d_model_in, d_model_out, kernel_size = 3, stride = 2, padding=1, norm_layer=False),
Rearrange('b c h w -> b h w c'),
)
self.model = nn.Sequential(
*[nn.Sequential(
PreNormResidual(d_model_in, nn.Sequential(
HireMLPBlock(
h, w, d_model_in, cross_region_step = cross_region_step, cross_region_id = i_depth + 1, cross_region_interval = cross_region_interval, padding_type = padding_type
)
), norm = nn.LayerNorm),
PreNormResidual(d_model_in, nn.Sequential(
nn.Linear(d_model_in, d_model_in * expansion_factor),
nn.GELU(),
nn.Dropout(dropout),
nn.Linear(d_model_in * expansion_factor, d_model_in),
nn.Dropout(dropout),
), norm = nn.LayerNorm),
) for i_depth in range(depth)]
)
def forward(self, x):
x = self.model(x)
if self.pooling:
x = self.patch_merge(x)
return x
class HireMLP(nn.Module):
def __init__(
self,
patch_size=4,
in_channels=3,
num_classes=1000,
d_model=[64, 128, 320, 512],
h = [4,3,3,2],
w = [4,3,3,2],
cross_region_step = [2,2,1,1],
cross_region_interval = 2,
depth=[4,6,24,3],
expansion_factor = 2,
patcher_norm = False,
padding_type = 'circular',
):
patch_size = pair(patch_size)
super().__init__()
self.patcher = PatchEmbedding(dim_in = in_channels, dim_out = d_model[0], kernel_size = 7, stride = patch_size, padding = 3, norm_layer=patcher_norm)
self.layers = nn.ModuleList()
for i_layer in range(len(depth)):
i_depth = depth[i_layer]
i_stage = HireMLPStage(h[i_layer], w[i_layer], d_model[i_layer], d_model_out = d_model[i_layer + 1] if (i_layer + 1 < len(depth)) else d_model[-1],
depth = i_depth, cross_region_step = cross_region_step[i_layer], cross_region_interval = cross_region_interval,
expansion_factor = expansion_factor, pooling = ((i_layer + 1) < len(depth)), padding_type = padding_type)
self.layers.append(i_stage)
self.mlp_head = nn.Sequential(
nn.LayerNorm(d_model[-1]),
Reduce('b h w c -> b c', 'mean'),
nn.Linear(d_model[-1], num_classes)
)
def forward(self, x):
embedding = self.patcher(x)
embedding = embedding.permute(0, 2, 3, 1)
for layer in self.layers:
embedding = layer(embedding)
out = self.mlp_head(embedding)
return out
