深度学习之图像分类（十七）-- Transformer中Self-Attention以及Multi-Head Attention详解

木卯 于 2021-09-08 发布

深度学习之图像分类（十七）Transformer中Self-Attention以及Multi-Head Attention详解

终于来到了 Transformer，从 2013 年分类网络学习到如今最火的 Transformer，真的不容易。本节学习 Transformer 中 Self-Attention 以及 Multi-Head Attention详解（注意不是 Version Transformer）。学习视频源于 Bilibili，博客参考 详解Transformer中Self-Attention以及Multi-Head Attention。建议先看一定李宏毅老师的讲解。

img0

1. 前言

Transformer 是 Google 在 2017 年发表于 Computation and Language 上的，其原始论文为 Attention Is All You Need。Transformer 一开始的提出是针对 NLP 领域的。在此之前主要用 RNN 和 LSTM 等时序网络，这些时序网络他们的问题在于，RNN 的记忆长度是有限的，比较短。此外，他们无法并行化，必须先计算 $t_0$ 时刻再计算 $t_1$ 时刻，是串行的关系，所以训练效率低。基于这些问题，Google 便提出了 Transformer 来解决这一系列问题。Transformer 在理论上不受硬件限制的话，记忆长度可以是无限长的；其次他是可以做并行化的。在这篇文章中作者提出了 Self-Attention 的概念，然后在此基础上提出 Multi-Head Attention。本节主要是对 Transformer 中的 Self-Attention 以及 Multi-Head Attention 进行讲解。

2. Self-Attention

过去我们经常看到这三张图以及对应的公式，但是还是很难理解是什么意思。李宏毅老师对此曾说：”看不懂的人，你再怎么看，还是看不懂“。

img2

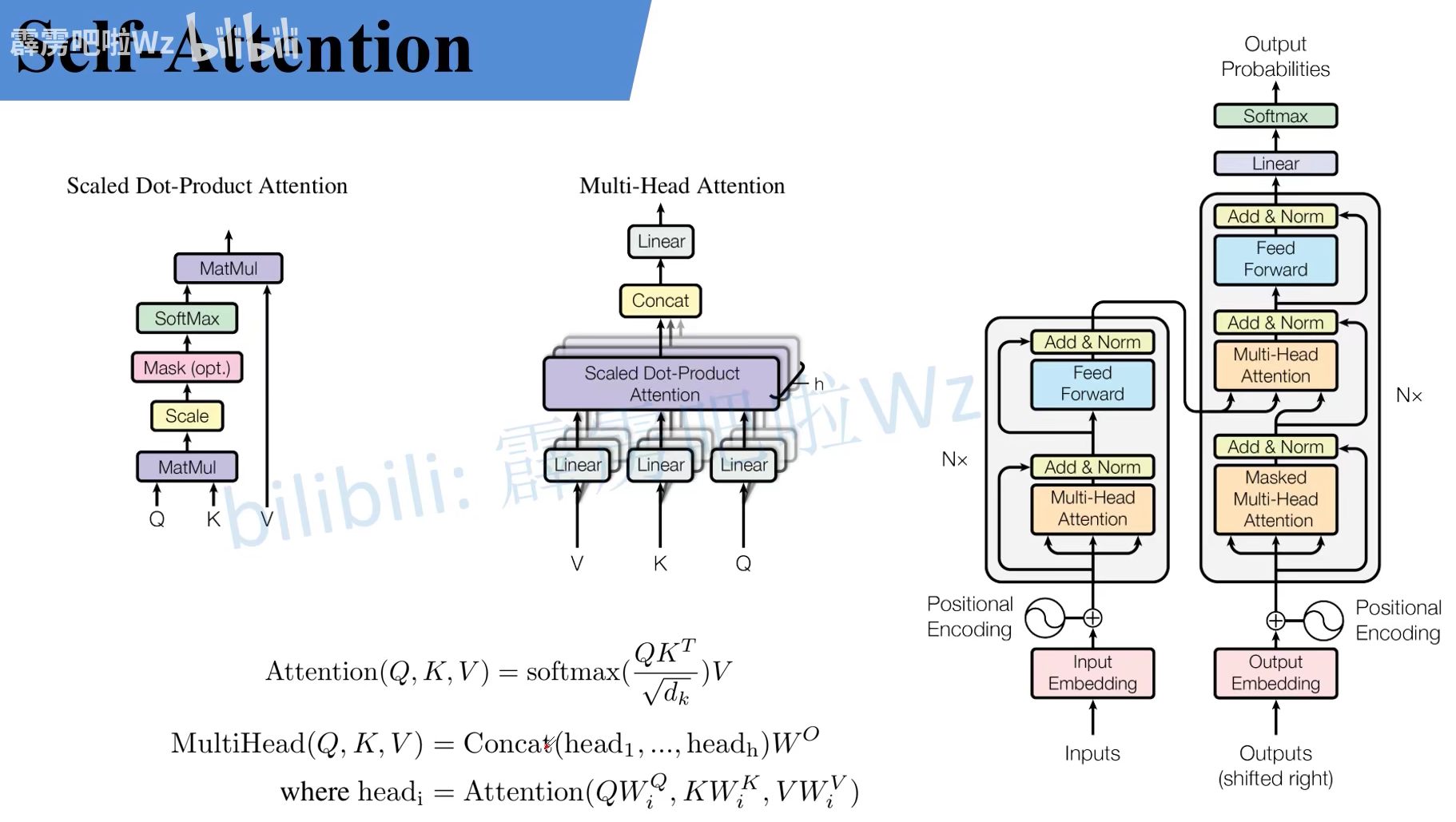
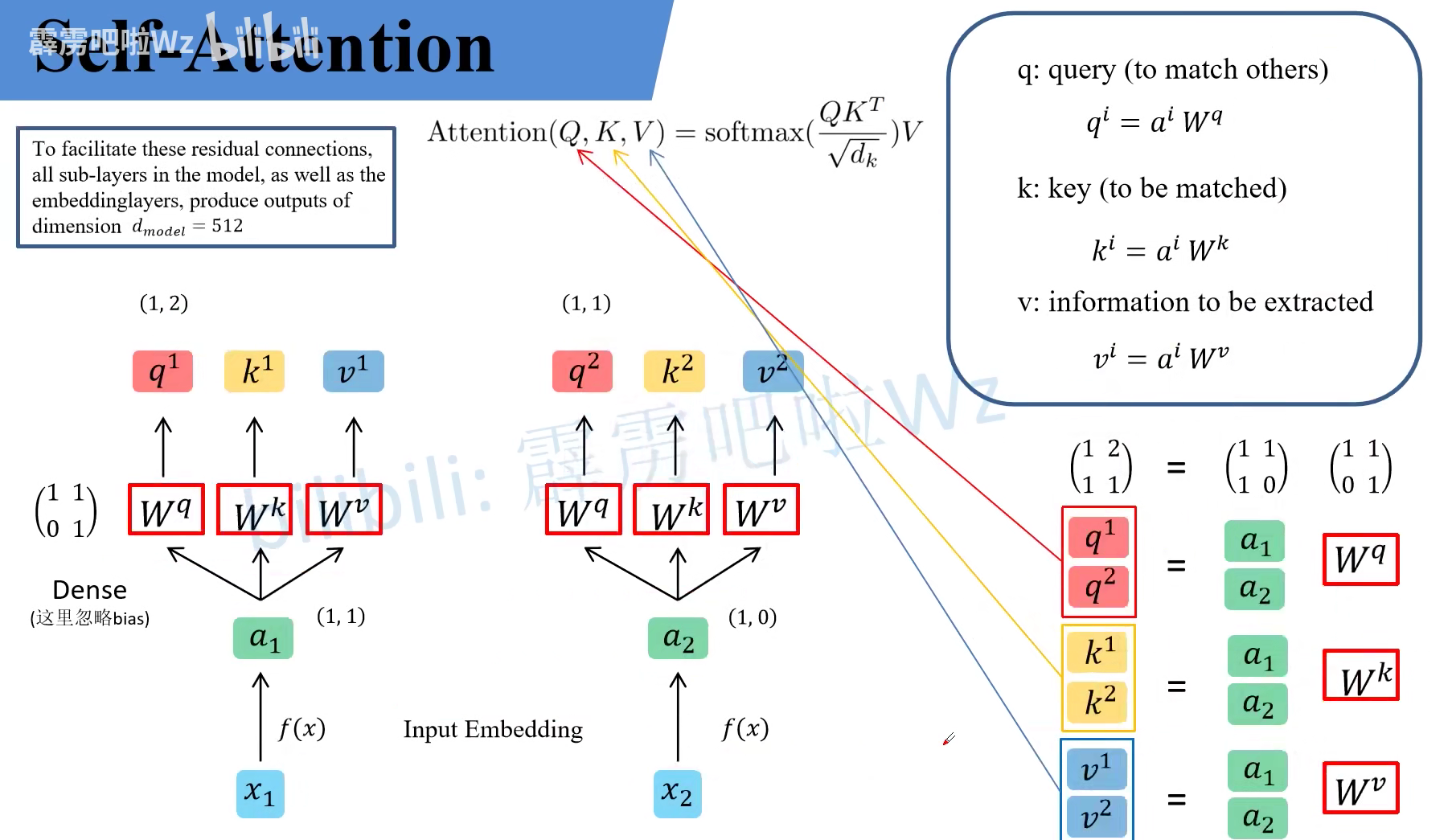
对此我们来进一步细讲它的理论。假如我们输入的时序数据是 $x$，例如这里的 $x_1$ 和 $x_2$。首先我们会把他们通过 Embedding 层映射到更高的维度上得到对应的 $a_1$ 和 $a_2$。紧接着将 $a$ 分别通过 $W^q, W^k, W^v$ 三个参数矩阵生成对应的 $q,k,v$。在网络中 $W^q, W^k, W^v$ 三个参数矩阵是共享的。在源码中， $W^q, W^k, W^v$ 其实直接通过全连接层来实现的，是可训练的参数。在这里讲的时候忽略偏置方便理解。假设 $a_1 = (1,1), a_2 = (1,0)$，然后再假设 $W^q$ 矩阵为 [[1, 1], [0, 1]]。根绝公式就可以得到 $q^1 = a_iW^q = (1,2)$，同理 $q^2 = (1,1)$。 \(q^{1}=(1,1)\left(\begin{array}{l} 1,1 \\ 0,1 \end{array}\right)=(1,2), \quad q^{2}=(1,0)\left(\begin{array}{l} 1,1 \\ 0,1 \end{array}\right)=(1,1)\) 这里的 $q$ 表达的含义是 query。也就是接下来他(query)会去匹配每一个 key。这里的 key 也是 $a$ 与 $W^k$ 进行相乘得到的。$v$ 则是从 $a$ 中提取得到的信息，他是 $a$ 与 $W^v$ 进行相乘得到的，也可理解为网络认为的从 $a$ 中提取到的有用的信息。由于在 Transformer 中是可并行化的，所以可以按照矩阵乘法的形式进行书写。例如 $a_1$ 和 $a_2$ 可以拼接到一起得到 [[1, 1], [1, 0]]。将 $q$ 全部放在一起就是 Attention 公式中的 Q，同理将 $k$ 和 $v$ 分别放在一起就是公式中的 $K$ 和 $V$。 \(\left(\begin{array}{l} q^{1} \\ q^{2} \end{array}\right)=\left(\begin{array}{l} 1,1 \\ 1,0 \end{array}\right)\left(\begin{array}{l} 1,1 \\ 0,1 \end{array}\right)=\left(\begin{array}{l} 1,2 \\ 1,1 \end{array}\right)\) img3

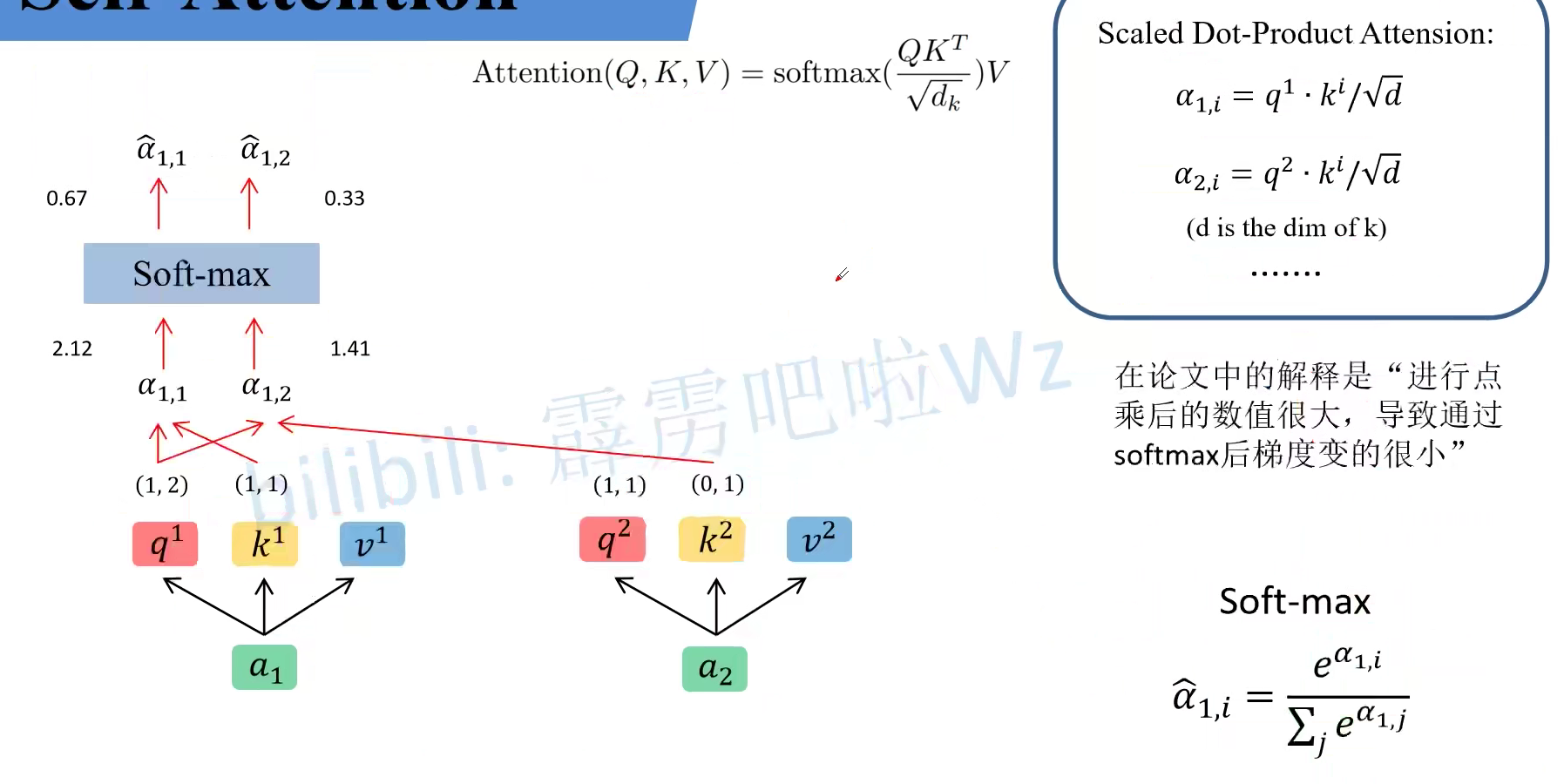
当得到 $Q,K,V$ 之后，就需要将 $q$ 与每一个 $k$ 进行 match 匹配，$\alpha_1,i = q^1 \cdot k^i / \sqrt{d}$，其中 $d$ 是 $k$ 的 dimension ($k$ 求出来其实是一个向量，所以其 dimension 就是向量中元素的个数，即向量的长度，在下图中为 2)。最终经过 Softmax 之后，得到的权重越大，我们就会关注对应的 $v$。 \(\begin{aligned} &\alpha_{1,1}=\frac{q^{1} \cdot k^{1}}{\sqrt{d}}=\frac{1 \times 1+2 \times 0}{\sqrt{2}}=0.71 \\ &\alpha_{1,2}=\frac{q^{1} \cdot k^{2}}{\sqrt{d}}=\frac{1 \times 0+2 \times 1}{\sqrt{2}}=1.41 \end{aligned}\) img4

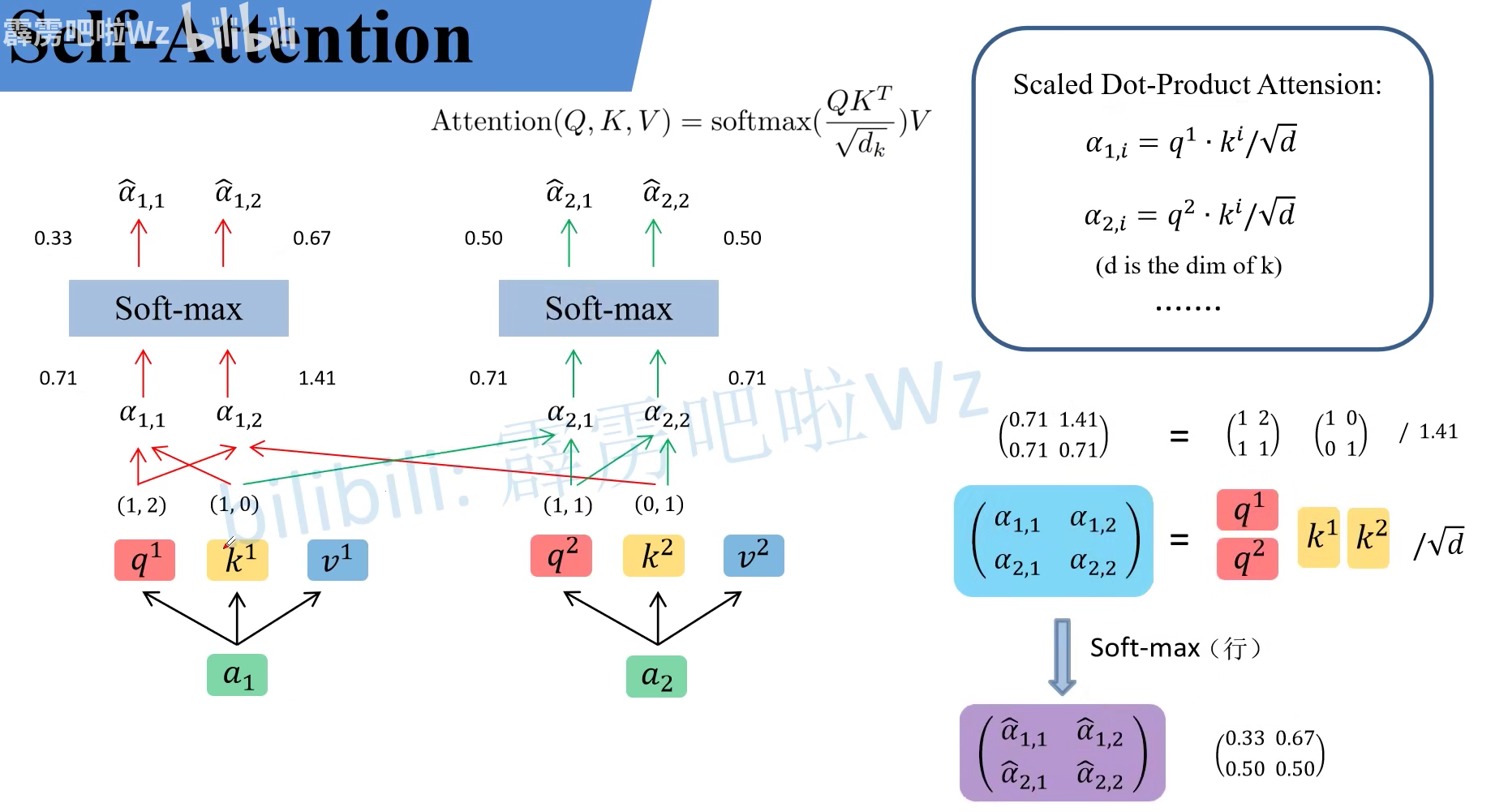
同样的我们也会拿 $q^2$ 和每个 key 进行匹配，同样可以得到 $\alpha_{2,1}$ 和 $\alpha_{2,2}$。经过 Softmax 就可以得到 $\hat{\alpha}{2,1}$ 和 $\hat{\alpha}{2,2}$。这个过程也是可以用矩阵乘法的形式来进行书写的，即 $QK^T$。 \(\left(\begin{array}{ll} \alpha_{1,1} & \alpha_{1,2} \\ \alpha_{2,1} & \alpha_{2,2} \end{array}\right)=\frac{\left(\begin{array}{l} q^{1} \\ q^{2} \end{array}\right)\left(\begin{array}{l} k^{1} \\ k^{2} \end{array}\right)^{T}}{\sqrt{d}}\) img5

$\hat{\alpha}$ 其实就是针对每一个 $v$ 的权重大小。所以接下来使用 $\hat{\alpha}$ 对 $v$ 进行进一步操作。即拿 $\hat{\alpha}{1,1}$ 与 $v^1$ 相乘加上拿 $\hat{\alpha}{1,2}$ 与 $v^2$ 相乘得 $b_1$，即拿 $\hat{\alpha}{2,1}$ 与 $v^1$ 相乘加上拿 $\hat{\alpha}{2,2}$ 与 $v^2$ 相乘得 $b_2$。这个过程也是可以用矩阵乘法的形式来进行书写的。 \(\begin{aligned} &b_{1}=\hat{\alpha}_{1,1} \times v^{1}+\hat{\alpha}_{1,2} \times v^{2}=(0.33,0.67) \\ &b_{2}=\hat{\alpha}_{2,1} \times v^{1}+\hat{\alpha}_{2,2} \times v^{2}=(0.50,0.50) \end{aligned} \\ \left(\begin{array}{l} b_{1} \\ b_{2} \end{array}\right)=\left(\begin{array}{ll} \hat{\alpha}_{1,1} & \hat{\alpha}_{1,2} \\ \hat{\alpha}_{2,1} & \hat{\alpha}_{2,2} \end{array}\right)\left(\begin{array}{l} v^{1} \\ v^{2} \end{array}\right)\) img6

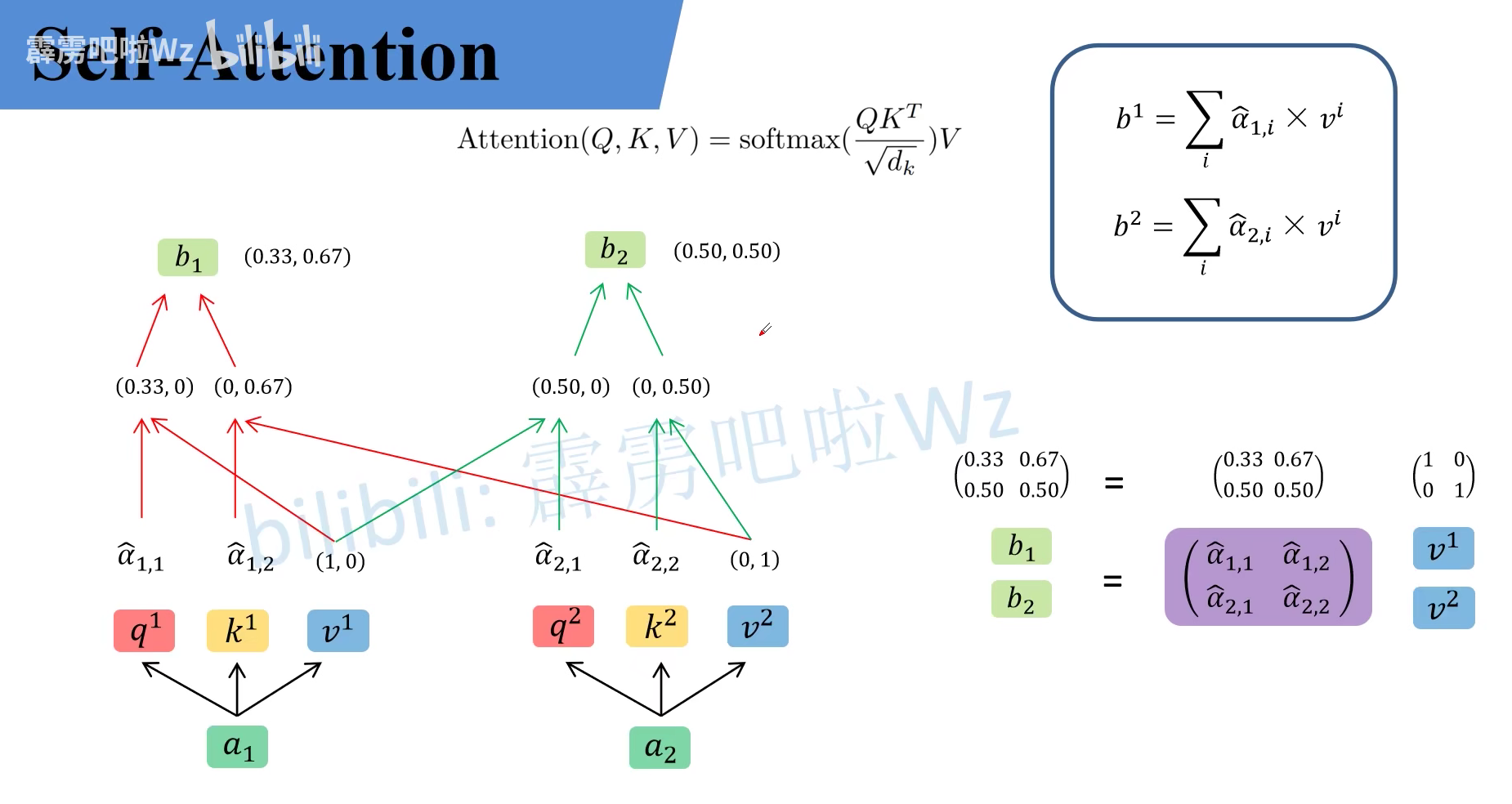
此时对于 Self-Attention 这个公式基本讲解完了。总结下来就是论文中的一个公式： \(\operatorname{Attention}(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{d_{k}}}\right) V\) 如果将其抽象为一个模块的话，可如下所示：

img7

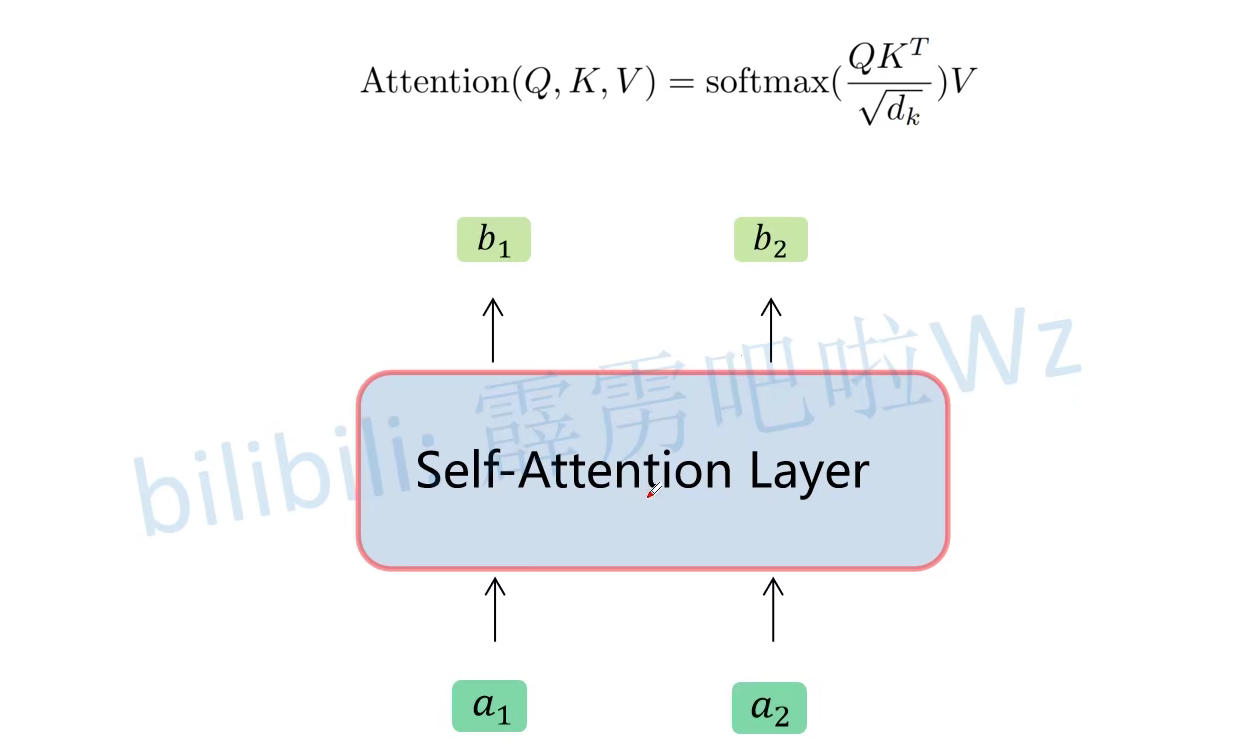
3. Multi-head Self-Attention

在 Transformer 使用过程中使用更多的其实还是 Multi-head Self-Attention。原论文中说使用多头注意力机制能够联合来自不同 head 部分学习到的信息。(Multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions.)

img8

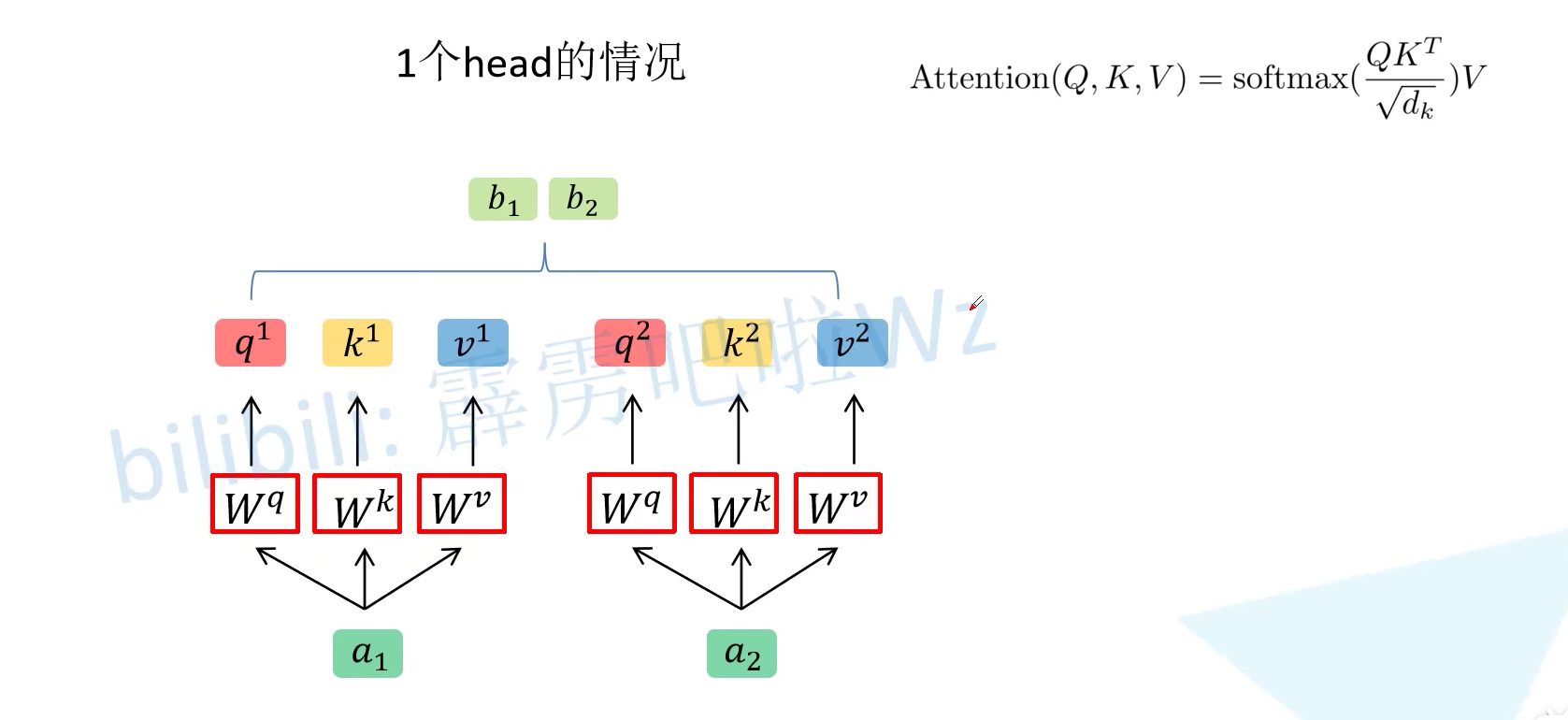
Multi-head Self-Attention 其实也非常简单，首先还是拿 $a$ 与 $W^q, W^k, W^v$ 相乘得到 $q,k,v$。然后我们根据 Head 对数据进行拆分。例如 $q^1 = (1,1,0,1)$，则将它拆分后得到$(1,1)$ 和 $(0,1)$。在源码中就是将 $q^1$ 均分给每个 Head。在论文中作者说通过线性映射得到的，其实可以直接理解为按照 head 的个数直接均分即可。 $$ \text { head }{i}=\text { Attention }\left(Q W{i}^{Q}, K W_{i}^{K}, V W_{i}^{V}\right) \

W_1^Q = W_1^K = W_1^V = \left(\begin{array}{l} 1,0
0,1
0,0
0,0
\end{array}\right) \quad W_2^Q = W_2^K = W_2^V = \left(\begin{array}{l} 0,0
0,0
1,0
0,1
\end{array}\right) $$ img9

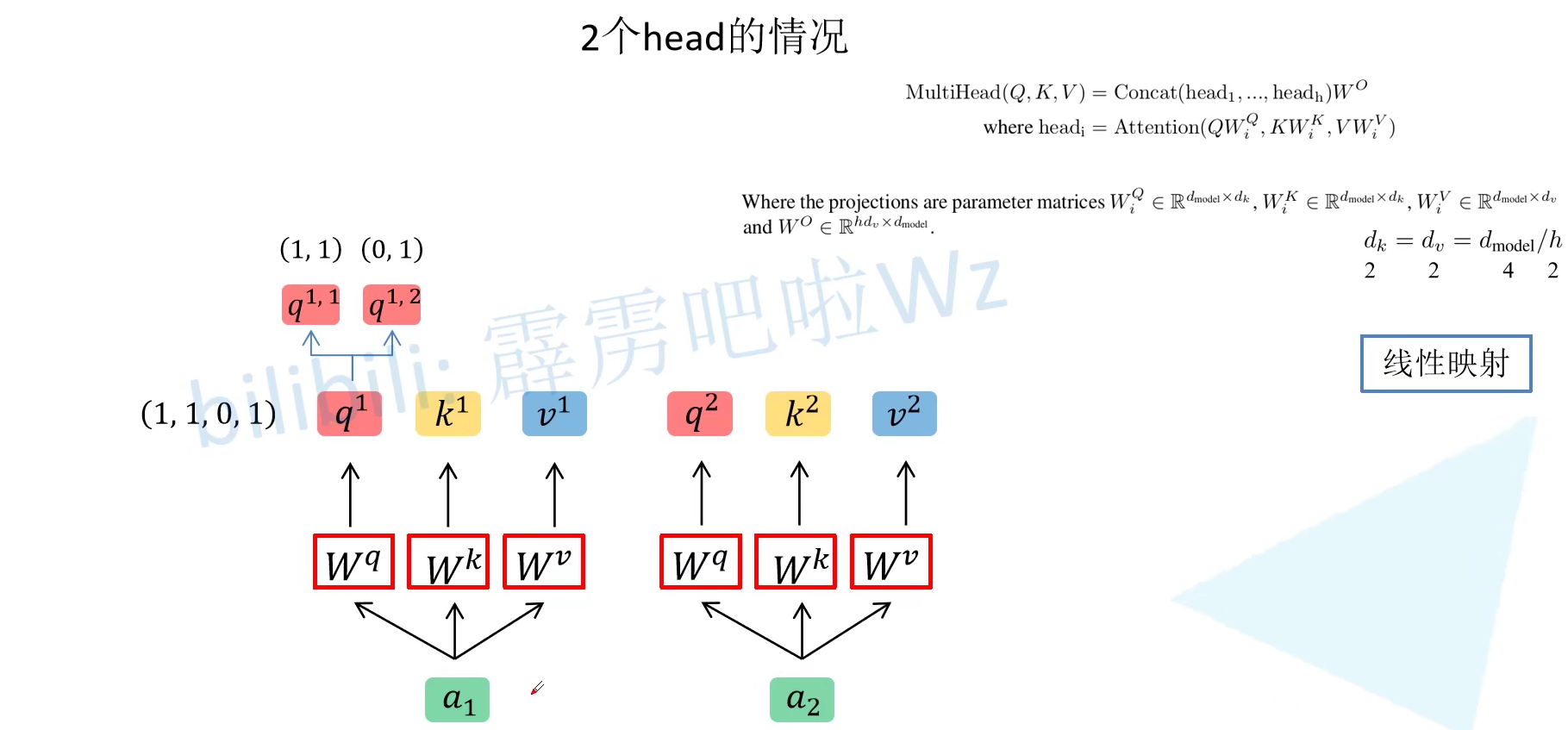
同理将所有的 $q,k,v$ 进行拆分，将第二个下标为 $1$ 的 $q,k,v$ (即 $q^{1,1},k^{1,1},v^{1,1},q^{2,1},k^{2,1},v^{2,1}$ ) 分配给 head 1，将第二个下标为 $2$ 的 $q,k,v$ (即 $q^{1,2},k^{1,2},v^{1,2},q^{2,2},k^{2,2},v^{2,2}$ ) 分配给 head 2。

img10

接下来对于每一个 Head 执行之前描述的 Self-Attention 中的一系列过程。 \(\operatorname{Attention}(Q_i, K_i, V_i)=\operatorname{softmax}\left(\frac{Q_i K_i^{T}}{\sqrt{d_{k}}}\right) V_i\) img11

然后将计算结果进行拼接即可。$b_{1,1}$ (head1 得到的 $b_1$) 和 $b_{1,2}$ (head2 得到的 $b_1$) 拼接在一起。$b_{2,1}$ (head1 得到的 $b_2$) 和 $b_{2,2}$ (head2 得到的 $b_2$) 拼接在一起。

img12

拼接后还需要通过 $W^O$ 将拼接后的数据进行融合得到最终 MultiHead 的输出。为了保证输入输出 multi-head attention 的向量长度保持不变，$W^O$ 的维度是 $hd_v \times d_{model}$，$hd_v$ 其实也等于 $d_{model}$。

img13

multi-head attention 其实和 group conv 很像啊！

总结下来就是论文中的两个公式： \(\begin{gathered} \operatorname{MultiHead}(Q, K, V)=\operatorname{Concat}\left(\operatorname{head}_{1}, \ldots, \text { head }_{\mathrm{h}}\right) W^{O} \\ \text { where head }_{\mathrm{i}}=\operatorname{Attention}\left(Q W_{i}^{Q}, K W_{i}^{K}, V W_{i}^{V}\right) \end{gathered}\) 如果将其抽象为一个模块的话，可如下所示：

img14

原论文章节3.2.2中最后有说 Self-Attention 和 Multi-Head Self-Attention 的计算量其实差不多。Due to the reduced dimension of each head, the total computational cost is similar to that of single-head attention with full dimensionality.

3. Positional Encoding

假设我们输入 $a_1.a_2,a_3$ 得到对应的 $b_1,b_2,b_3$ ；如果将 $a_3,a_2$ 的顺序进行调换，对于 $b_1$ 而言是没有任何影响的。无论后面顺序如何是不影响 $b_1$ 的，但是实际这个是有问题的。所以引入了位置编码的思想。

img15

下面是使用 Pytorch 做的一个实验，首先使用 nn.MultiheadAttention 创建一个 Self-Attention 模块（num_heads=1），注意这里在正向传播过程中直接传入 $Q,K,V$，接着创建两个顺序不同的 $Q,K,V$ 变量 t1 和 t2（主要是将 $q^2, k^2, v^2$ 和 $q^3, k^3, v^3$ 的顺序换了下）。对比结果可以发现，对于 $b_1$ 是没有影响的， $b_2$ 和 $b_3$ 的顺序调换了。

import torch
import torch.nn as nn


m = nn.MultiheadAttention(embed_dim=2, num_heads=1)

t1 = [[[1., 2.],   # q1, k1, v1
       [2., 3.],   # q2, k2, v2
       [3., 4.]]]  # q3, k3, v3

t2 = [[[1., 2.],   # q1, k1, v1
       [3., 4.],   # q3, k3, v3
       [2., 3.]]]  # q2, k2, v2

q, k, v = torch.as_tensor(t1), torch.as_tensor(t1), torch.as_tensor(t1)
print("result1: \n", m(q, k, v))

q, k, v = torch.as_tensor(t2), torch.as_tensor(t2), torch.as_tensor(t2)
print("result2: \n", m(q, k, v))

img17

对于每一个 $a_i$ 会加一个 shape 一样的位置编码。可以根据论文公式进行计算得到位置编码，也可以训练得到位置编码。

img16