深度学习之图像分类(十三)ShuffleNetV1 网络结构
本节学习 ShuffleNetV1 网络结构。学习视频源于 Bilibili。

1. 前言
ShuffleNetV1 是由国产旷视科技团队在 2018 年提出的,其原始论文为 ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices。ShuffleNetV1 主要在于提出了 Channel Shuffle 的思想,shuffleNet Unit 中全是 Group Conv 以及 DW Conv。
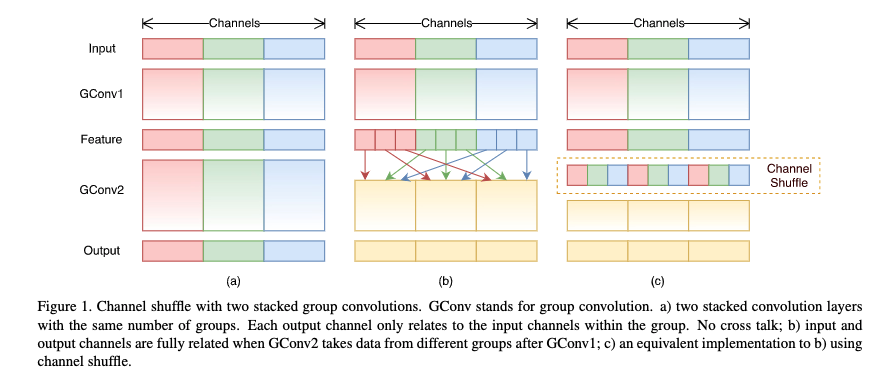
我们先来看一下作者在原论文中给出的性能指标。在骁龙820的处理器上,shuffleNet 0.5x 的错误率与 AlexNet 相当,但是推理速度为原来的十倍,通过对比能发现它有多么轻量级。suffleNet 2x 在推理速度和 MobileNet V1 相当的情况下,准确率要更好。
2. Channel Shuffle
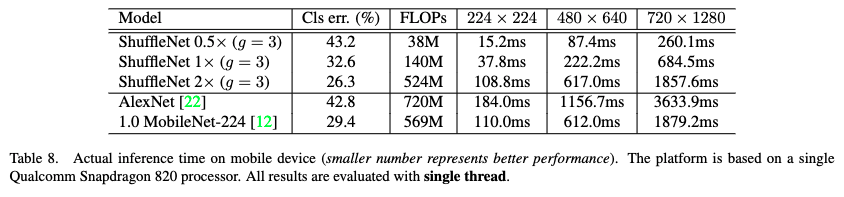
对于普通组卷积,如下图 a 所示,都是针对该组内的 channel 信息进行卷积操作,如果简单串联的话,则一直对同一个组内的信息进行处理,可以看到组与组之间是没有信息交流的,这样效果不好。为了解决这个问题,作者提出了 channel shuffle 这个概念。首先还是进行组卷积得到特征矩阵,假设我们使用三个 group,如下图 b 所示。然后对特征矩阵原来的 group 再进行更细粒度的划分成三个 sub-group,将每个组中的第一个 sub-group 放到一起,将每个组中的第二个 sub-group 放到一起…,就能形成新的特征矩阵。这时候再进行组卷积,就使得组与组之间的信息得到交流了。利用 Channel Shuffle 就可以充分发挥 Group conv 的优点,而避免其缺点。
我们再来看一下原论文中的某些论述。作者发现在 ResNeXt 中,$1 \times 1$ 的普通卷积占据了总计算量的 93.4%。

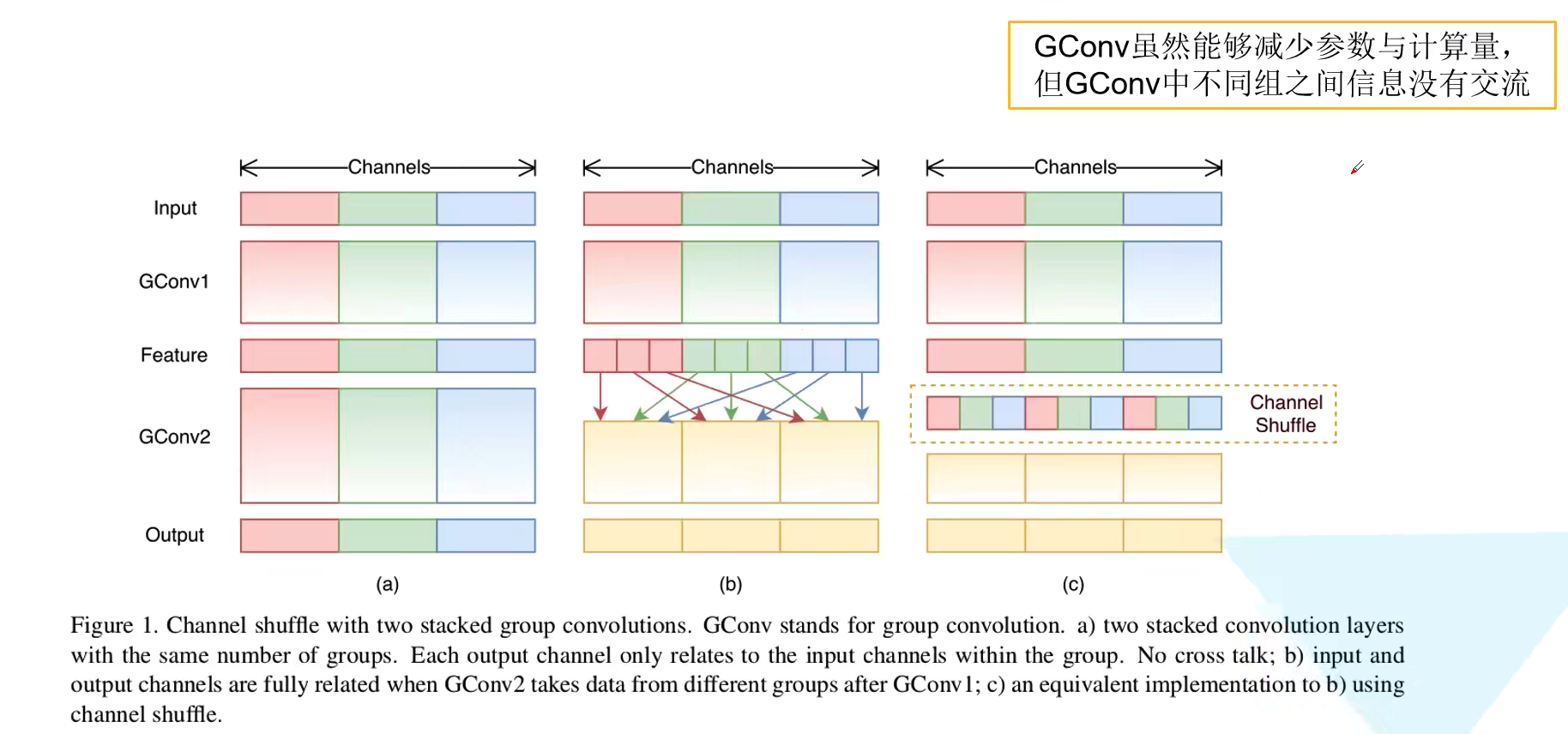
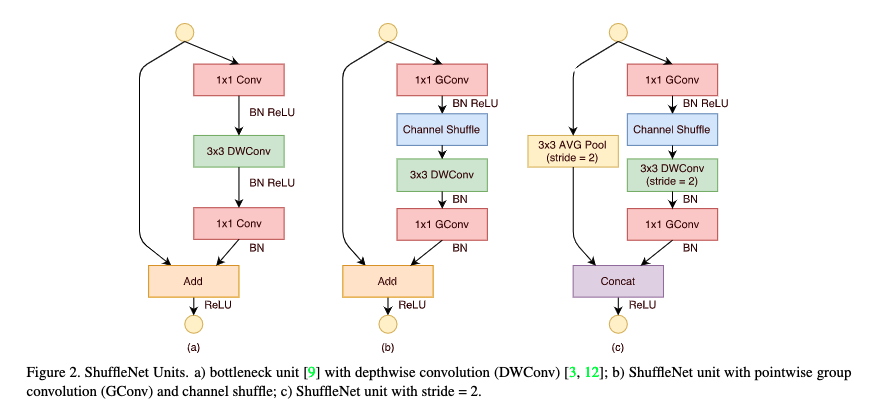
所以在 shuffleNetV1 网络中作者将所有的 $1 \times 1$ 卷积都替换为了 $1 \times 1$ Group 卷积,并且在第一个 $1 \times 1$ Group 卷积之后进行 channel shuffle 操作。下图 c 则展示了 stride = 2 时候的 block,注意当 stride = 2 时是通道 concat 在一起的,而不是残差做加法。
Channel Shuffle 如何实现?注意到,shuffleNetV1 实现的是均匀的 shuffle。所以在程序上实现 Channel Shuffle 是非常容易的:假定将输入层分为 $g$ 组,保证总通道数是 $g$ 的倍数,例如为 $g \times n$ ,首先你将通道那个维度拆分为 $(g, n)$ 两个维度,然后将这两个维度转置变成 $(n, g)$ 两个维度,最后重新 reshape 成一个维度。相当于之前通道方向是一个一维向量,变成 $g \times n$ 的矩阵,每行是一个 group,一个 group 内有 n 个元素。然后把矩阵转置 $n \times g$ ,此时的每一行相当于原来的每一列,再转回原来的一维向量。如果现在看成 g 个 group,则是把原来 group 的第 $i + j \times g$ 元素拿出来组成一个新的第 $i$ 个 group。一般而言,$n$ 是 $g$ 的倍数就实现了真正的“共产主义”平均了,如果 $n$ 不是 $g$ 的倍数,例如 $n = 5, g = 3$,其实也还好,原来的三组是 $[a_1, a_2, a_3, a_4, a_5],[b_1, b_2, b_3, b_4, b_5],[c_1, c_2, c_3, c_4, c_5]$,现在是 $[a_1, b_1, c_1, a_2, b_2],[c_2, a_3, b_3, c_3, a_4],[b_4, c_4, a_5, b_5, c_5]$。实现代码如下:
def channel_shuffle(x, groups):
batchsize, num_channels, height, width = x.data.size()
channels_per_group = num_channels // groups# groups是分的组数
# reshape
x = x.view(batchsize, groups,
channels_per_group, height, width)
# transpose
# - contiguous() required if transpose() is used before view().
# See https://github.com/pytorch/pytorch/issues/764
x = torch.transpose(x, 1, 2).contiguous()
# flatten
x = x.view(batchsize, -1, height, width)
return x
3. ShuffleNetV1 网络结构
下图给出了 ShuffleNetV1 的网络结构。我们主要关注 g = 3 的版本,原论文很多实验也是基于 g = 3 来进行的,g 对应着 group 卷积的 group 数。每一个 stage 给出了使用 block 的 stride 以及重复次数。最后通过全局池化和全连接层得到最终的输出。

有几个注意的关键点,每个 stage 的第一个 block 都是步距为 2。对于下一个 stage 的输出通道会进行一个翻倍的操作。与 ResNet 一致,将第一个 $1 \times 1$ Group 卷积降维的输出通道数设定为 block 输出通道数的 1/4,对应于左下角的图。此外,对于 stage2 的第一个 block 的第一个 $1 \times 1$ 卷积并不使用 group conv,因为输入的 24 通道特别小。
我们再看一下原论文中给出的关于 FLOPs 的一些计算。假设输入每个特征矩阵是 $c \times h \times w$,假设第一个 $1 \times 1$ 卷积和 $3 \times 3$ 卷积的输出通道为 $m$ ,最终的输出通道数为 $c$,stride = 1 。我们就能计算出使用 ResNet ,ResNeXt 以及 ShuffleNetV1 中使用的 block 的 FLOPs。这里注意,组卷积的计算量输入输出通道都要除以组数 g,但是有 g 个组,所以还要乘一个 g,整体而言就是除以一个 g。DW conv 其实就是 g = m。
\[\text { ResNet : } \quad h w(1 \times 1 \times c \times m)+h w(3 \times 3 \times m \times m)+h w(1 \times 1 \times m \times c)=h w\left(2 \mathrm{~cm}+9 m^{2}\right) \\ \text { ResNeXt : } \quad h w(1 \times 1 \times c \times m)+h w(3 \times 3 \times m \times m) / g+h w(1 \times 1 \times m \times c)=h w\left(2 c m+9 m^{2} / g\right) \\ \text { ShuffleNet: } \quad h w(1 \times 1 \times c \times m) / g+h w(3 \times 3 \times m)+h w(1 \times 1 \times m \times c) / g=h w(2 c m / g+9m)\]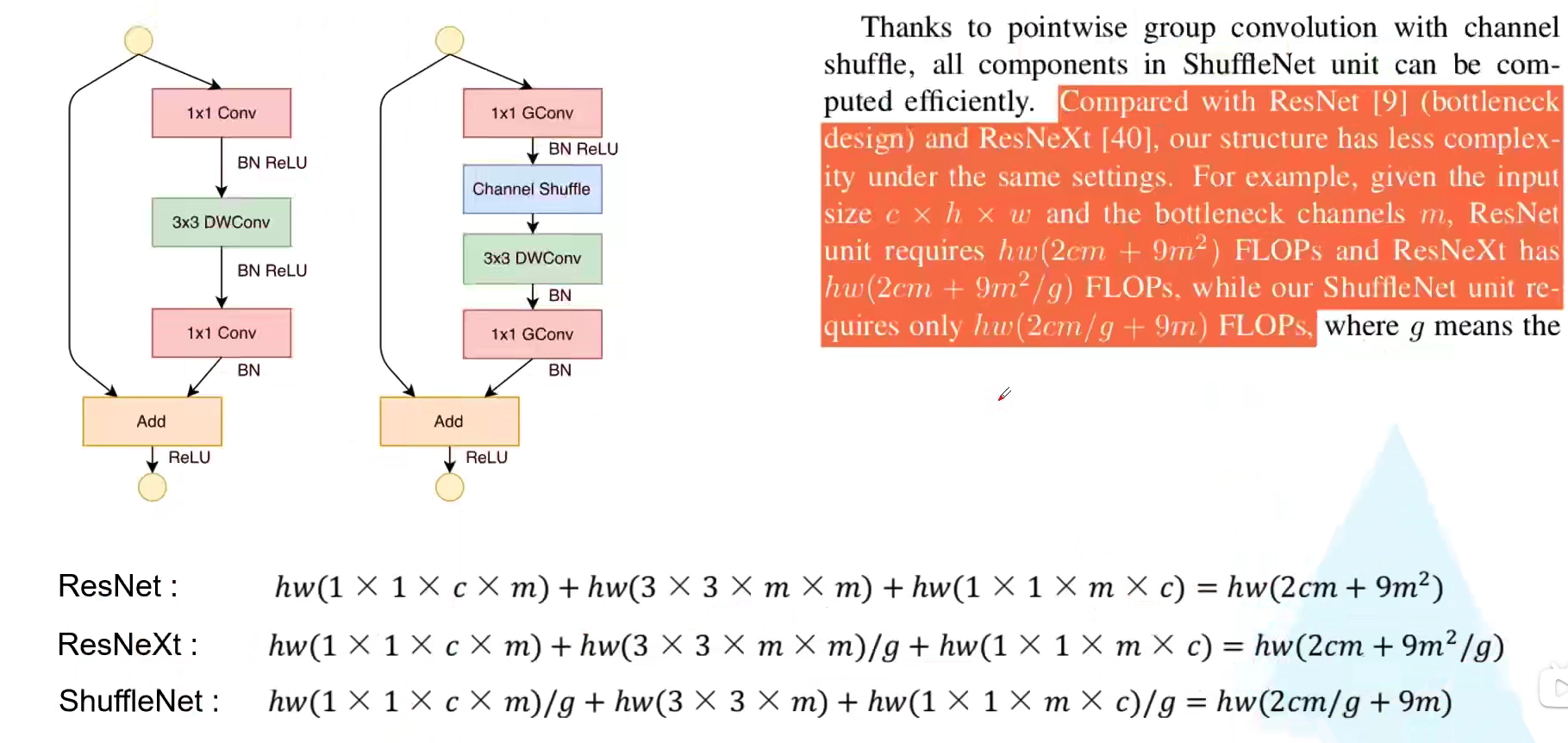
补充一些基础知识:
FLOPS 全大写,指的是每秒浮点数运算次数,可以理解为计算的速度,是衡量硬件性能的一个指标(硬件)
FLOPs s小写,指的是浮点运算数,理解为计算量,可以用来衡量算法/模型的复杂度(模型)
论文中常用的 MFLOPs,1MFLOPs = 10^6 FLOPs
论文中常用的 GFLOPs,1GFLOPs = 10^9 FLOPs
但是计算复杂度不能只看 FLOPs,还要参考一些其他指标
但是 shuffleNet 也有两个缺点:
- Channel Shuffle 在实现的时候需要大量的指针跳转和 Memory set,这本身就是极其耗时的;同时又特别依赖实现细节,导致实际运行速度不会那么理想。
- Channel Shuffle 的规则是人定的,每个通道都需要等量地交换信息,不一定是最优的,不是网络自己学出来的。
4. 代码
ShuffleNetV1 实现代码如下所示,代码来源:
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.autograd import Variable
from collections import OrderedDict
from torch.nn import init
def conv3x3(in_channels, out_channels, stride=1,
padding=1, bias=True, groups=1):
"""3x3 convolution with padding
"""
return nn.Conv2d(
in_channels,
out_channels,
kernel_size=3,
stride=stride,
padding=padding,
bias=bias,
groups=groups)
def conv1x1(in_channels, out_channels, groups=1):
"""1x1 convolution with padding
- Normal pointwise convolution When groups == 1
- Grouped pointwise convolution when groups > 1
"""
return nn.Conv2d(
in_channels,
out_channels,
kernel_size=1,
groups=groups,
stride=1)
def channel_shuffle(x, groups):
batchsize, num_channels, height, width = x.data.size()
channels_per_group = num_channels // groups# groups是分的组数
# reshape
x = x.view(batchsize, groups,
channels_per_group, height, width)
# transpose
# - contiguous() required if transpose() is used before view().
# See https://github.com/pytorch/pytorch/issues/764
x = torch.transpose(x, 1, 2).contiguous()
# flatten
x = x.view(batchsize, -1, height, width)
return x
class ShuffleUnit(nn.Module):
def __init__(self, in_channels, out_channels, groups=3,
grouped_conv=True, combine='add'):
super(ShuffleUnit, self).__init__()
self.in_channels = in_channels
self.out_channels = out_channels
self.grouped_conv = grouped_conv
self.combine = combine
self.groups = groups
self.bottleneck_channels = self.out_channels // 4
# define the type of ShuffleUnit
if self.combine == 'add':
# ShuffleUnit Figure 2b
self.depthwise_stride = 1
self._combine_func = self._add
elif self.combine == 'concat':
# ShuffleUnit Figure 2c
self.depthwise_stride = 2
self._combine_func = self._concat
# ensure output of concat has the same channels as
# original output channels.
self.out_channels -= self.in_channels
else:
raise ValueError("Cannot combine tensors with \"{}\"" \
"Only \"add\" and \"concat\" are" \
"supported".format(self.combine))
# Use a 1x1 grouped or non-grouped convolution to reduce input channels
# to bottleneck channels, as in a ResNet bottleneck module.
# NOTE: Do not use group convolution for the first conv1x1 in Stage 2.
self.first_1x1_groups = self.groups if grouped_conv else 1
self.g_conv_1x1_compress = self._make_grouped_conv1x1(
self.in_channels,
self.bottleneck_channels,
self.first_1x1_groups,
batch_norm=True,
relu=True
)
# 3x3 depthwise convolution followed by batch normalization
self.depthwise_conv3x3 = conv3x3(
self.bottleneck_channels, self.bottleneck_channels,
stride=self.depthwise_stride, groups=self.bottleneck_channels)
self.bn_after_depthwise = nn.BatchNorm2d(self.bottleneck_channels)
# Use 1x1 grouped convolution to expand from
# bottleneck_channels to out_channels
self.g_conv_1x1_expand = self._make_grouped_conv1x1(
self.bottleneck_channels,
self.out_channels,
self.groups,
batch_norm=True,
relu=False
)
@staticmethod
def _add(x, out):
# residual connection
return x + out
@staticmethod
def _concat(x, out):
# concatenate along channel axis
return torch.cat((x, out), 1)
def _make_grouped_conv1x1(self, in_channels, out_channels, groups,
batch_norm=True, relu=False):
modules = OrderedDict()
conv = conv1x1(in_channels, out_channels, groups=groups)
modules['conv1x1'] = conv
if batch_norm:
modules['batch_norm'] = nn.BatchNorm2d(out_channels)
if relu:
modules['relu'] = nn.ReLU()
if len(modules) > 1:
return nn.Sequential(modules)
else:
return conv
def forward(self, x):
# save for combining later with output
residual = x
if self.combine == 'concat':
residual = F.avg_pool2d(residual, kernel_size=3,
stride=2, padding=1)
out = self.g_conv_1x1_compress(x)
out = channel_shuffle(out, self.groups)
out = self.depthwise_conv3x3(out)
out = self.bn_after_depthwise(out)
out = self.g_conv_1x1_expand(out)
out = self._combine_func(residual, out)
return F.relu(out)
class ShuffleNet(nn.Module):
"""ShuffleNet implementation.
"""
def __init__(self, groups=3, in_channels=3, num_classes=1000):
"""ShuffleNet constructor.
Arguments:
groups (int, optional): number of groups to be used in grouped
1x1 convolutions in each ShuffleUnit. Default is 3 for best
performance according to original paper.
in_channels (int, optional): number of channels in the input tensor.
Default is 3 for RGB image inputs.
num_classes (int, optional): number of classes to predict. Default
is 1000 for ImageNet.
"""
super(ShuffleNet, self).__init__()
self.groups = groups
self.stage_repeats = [3, 7, 3]
self.in_channels = in_channels
self.num_classes = num_classes
# index 0 is invalid and should never be called.
# only used for indexing convenience.
if groups == 1:
self.stage_out_channels = [-1, 24, 144, 288, 567]
elif groups == 2:
self.stage_out_channels = [-1, 24, 200, 400, 800]
elif groups == 3:
self.stage_out_channels = [-1, 24, 240, 480, 960]
elif groups == 4:
self.stage_out_channels = [-1, 24, 272, 544, 1088]
elif groups == 8:
self.stage_out_channels = [-1, 24, 384, 768, 1536]
else:
raise ValueError(
"""{} groups is not supported for
1x1 Grouped Convolutions""".format(num_groups))
# Stage 1 always has 24 output channels
self.conv1 = conv3x3(self.in_channels,
self.stage_out_channels[1], # stage 1
stride=2)
self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
# Stage 2
self.stage2 = self._make_stage(2)
# Stage 3
self.stage3 = self._make_stage(3)
# Stage 4
self.stage4 = self._make_stage(4)
# Global pooling:
# Undefined as PyTorch's functional API can be used for on-the-fly
# shape inference if input size is not ImageNet's 224x224
# Fully-connected classification layer
num_inputs = self.stage_out_channels[-1]
self.fc = nn.Linear(num_inputs, self.num_classes)
self.init_params()
def init_params(self):
for m in self.modules():
if isinstance(m, nn.Conv2d):
init.kaiming_normal(m.weight, mode='fan_out')
if m.bias is not None:
init.constant(m.bias, 0)
elif isinstance(m, nn.BatchNorm2d):
init.constant(m.weight, 1)
init.constant(m.bias, 0)
elif isinstance(m, nn.Linear):
init.normal(m.weight, std=0.001)
if m.bias is not None:
init.constant(m.bias, 0)
def _make_stage(self, stage):
modules = OrderedDict()
stage_name = "ShuffleUnit_Stage{}".format(stage)
# First ShuffleUnit in the stage
# 1. non-grouped 1x1 convolution (i.e. pointwise convolution)
# is used in Stage 2. Group convolutions used everywhere else.
grouped_conv = stage > 2
# 2. concatenation unit is always used.
first_module = ShuffleUnit(
self.stage_out_channels[stage-1],
self.stage_out_channels[stage],
groups=self.groups,
grouped_conv=grouped_conv,
combine='concat'
)
modules[stage_name+"_0"] = first_module
# add more ShuffleUnits depending on pre-defined number of repeats
for i in range(self.stage_repeats[stage-2]):
name = stage_name + "_{}".format(i+1)
module = ShuffleUnit(
self.stage_out_channels[stage],
self.stage_out_channels[stage],
groups=self.groups,
grouped_conv=True,
combine='add'
)
modules[name] = module
return nn.Sequential(modules)
def forward(self, x):
x = self.conv1(x)
x = self.maxpool(x)
x = self.stage2(x)
x = self.stage3(x)
x = self.stage4(x)
# global average pooling layer
x = F.avg_pool2d(x, x.data.size()[-2:])
# flatten for input to fully-connected layer
x = x.view(x.size(0), -1)
x = self.fc(x)
return x
