深度学习之图像分类(九)ResNeXt 网络结构
本节学习 ResNeXt 网络结构,以及组卷积原理。学习视频源于 Bilibili。
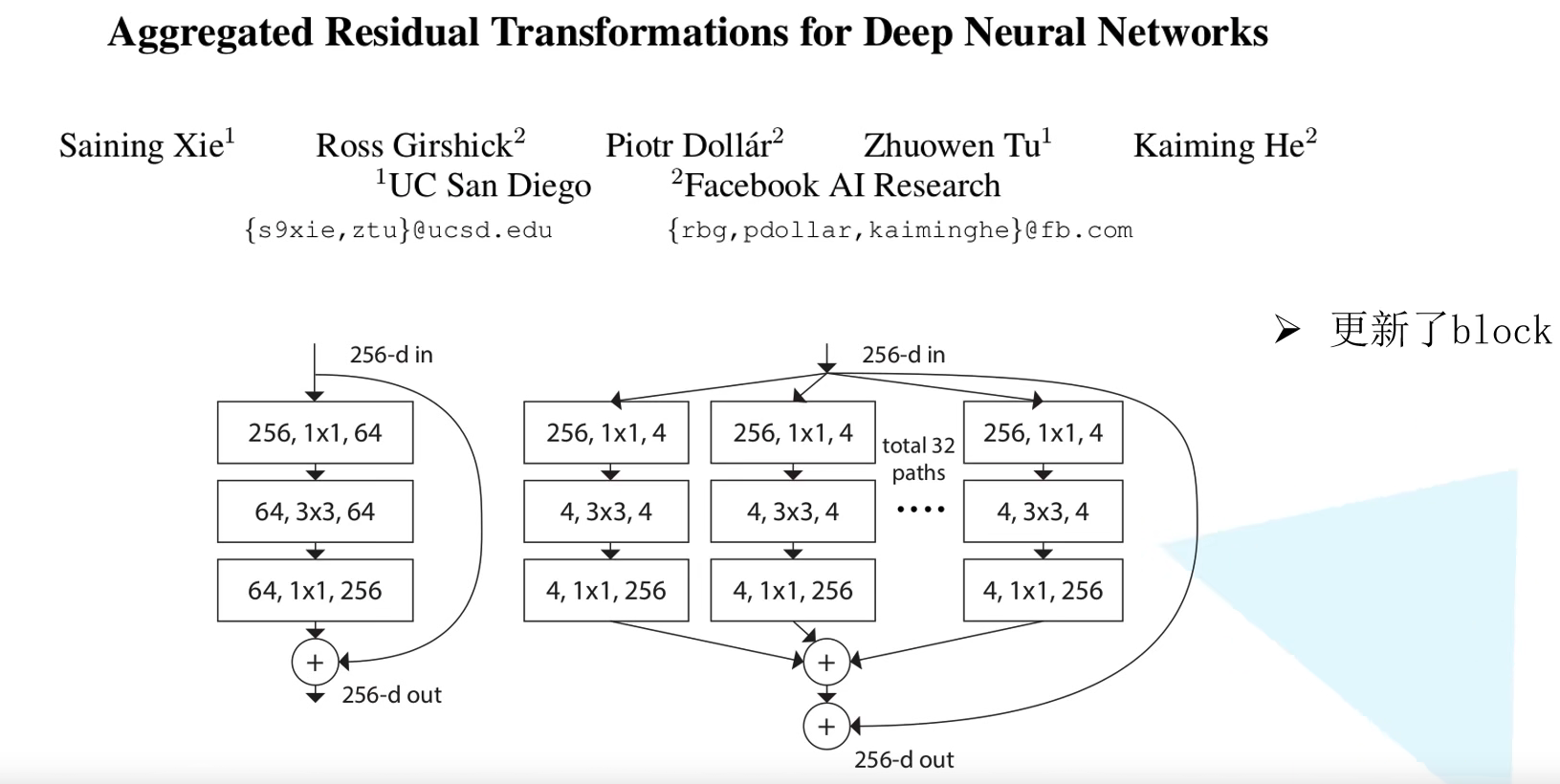
1. 前言
在提出 ResNet 网络之后,很多模型都会拿 ResNet 网络作为基准和比对。本章讲述的 ResNeXt 网络可以被视作对 ResNet 的小幅升级,其实不难发现其也参考了 Inception 的思想。其原始论文为 Aggregated Residual Transformations for Deep Neural Network,发表于 2017 年的 CVPR。但是这篇论文没有当初的 ResNet 那么惊艳了。本论文最大的贡献点就在于更新了 Residual Block,采用 split-transform-merge 策略,本质是分组卷积,但是不需要像 Inception 一样人工设计复杂的结构,也不像 Inception 一样结合不同尺寸感受野的信息,拓扑结构一致的 ResNeXt 对 GPU 等硬件也更友好 (所以这个结构跑得更快)。
值得指出的是,split-transform-merge 策略其实在 VGG 堆叠的思想和 Inception 的思想中都有体现,只不过 VGG split 的是变换函数本身,ResNeXt 和 Inception 都是 split 输入特征。
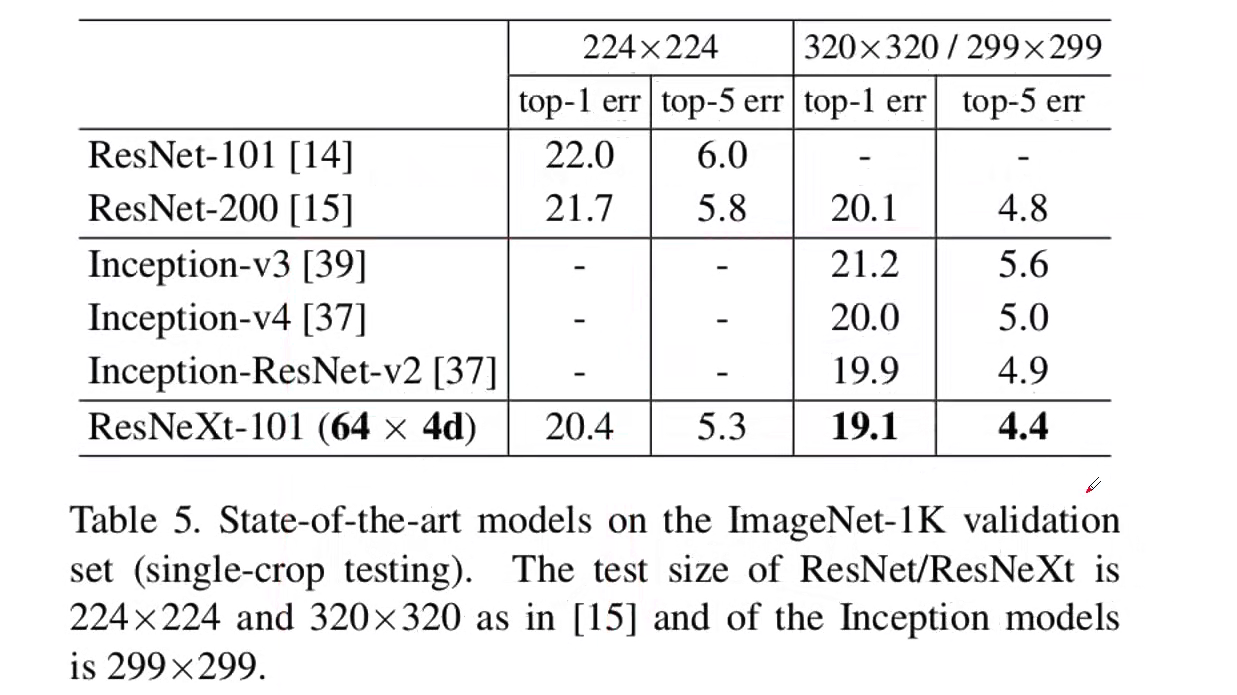
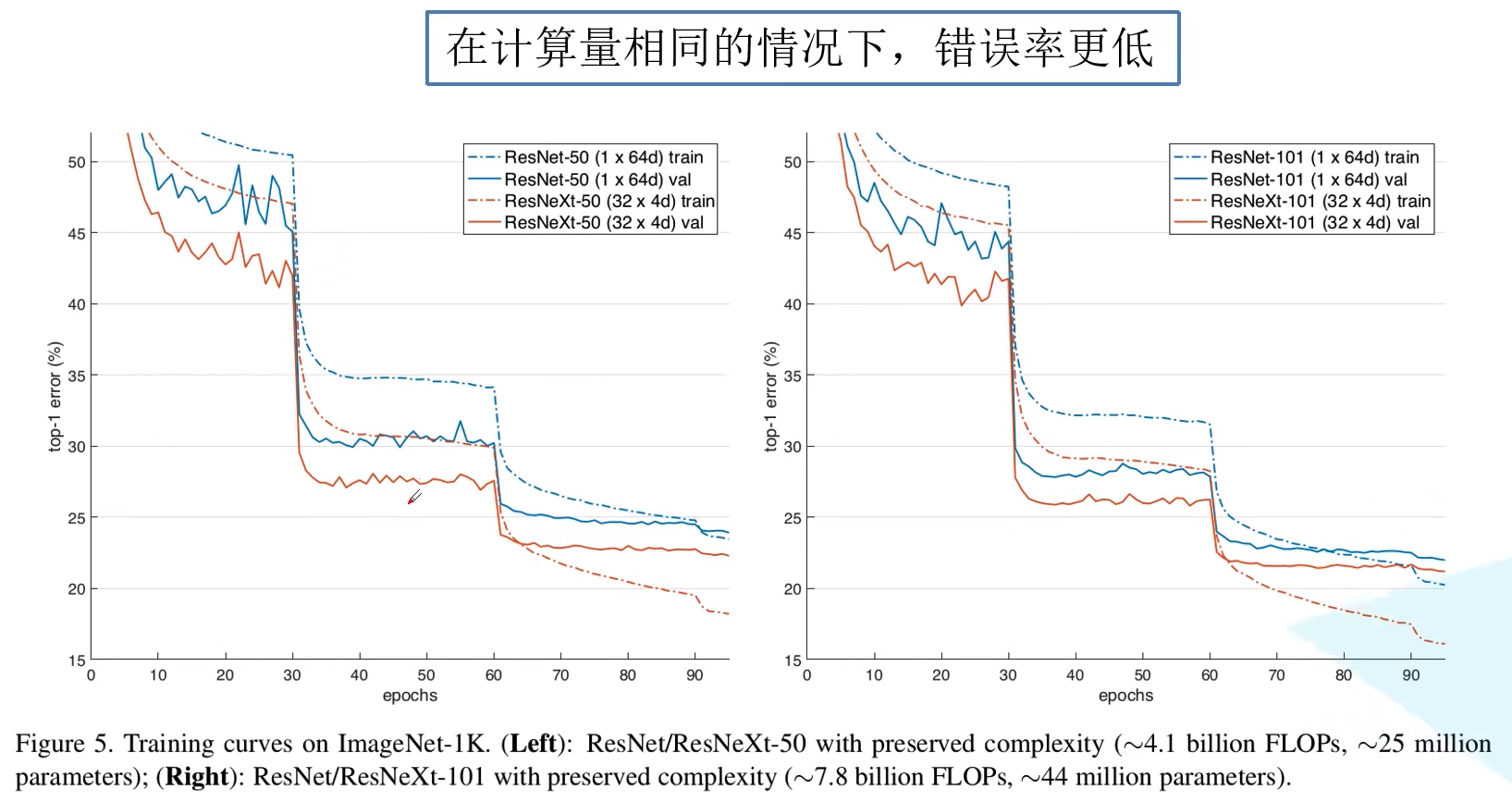
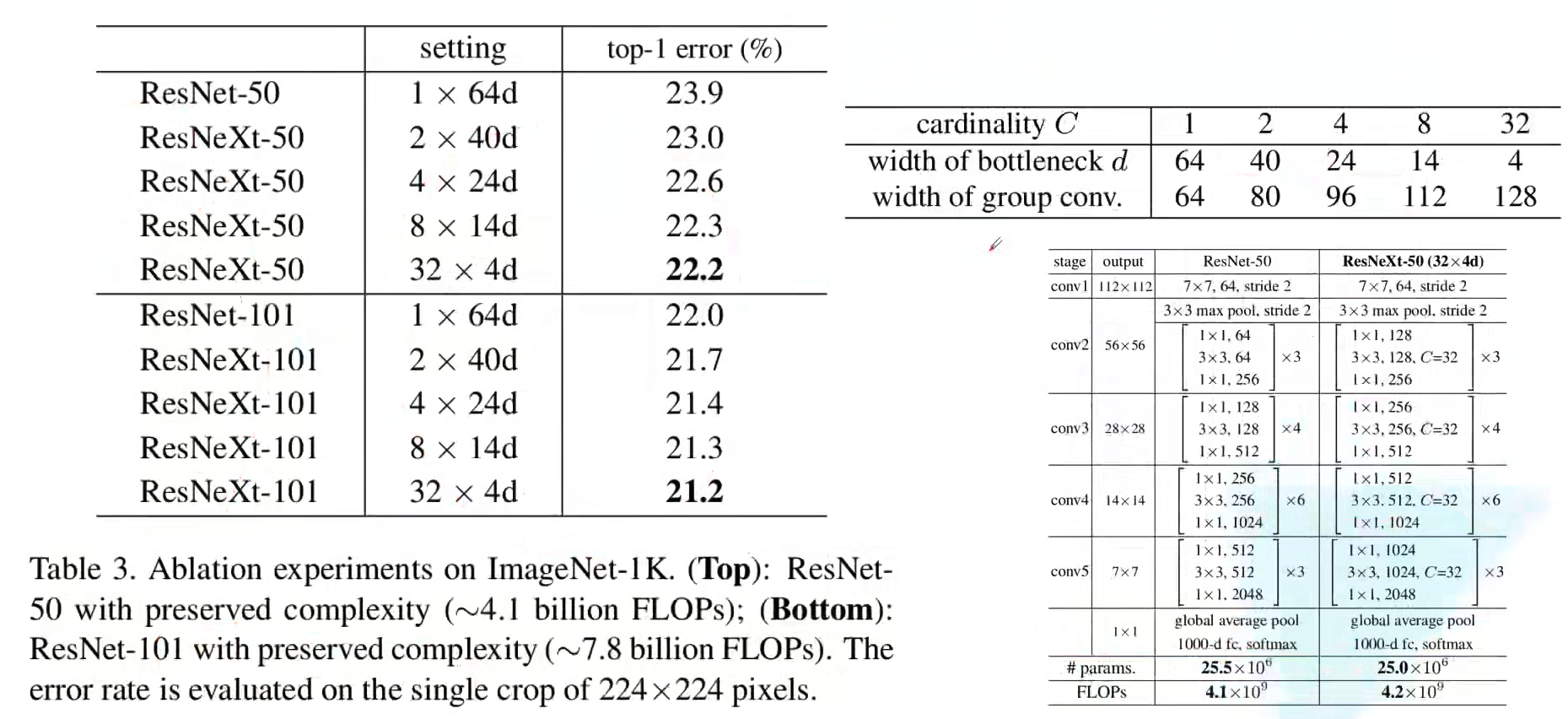
最终性能参数指标如图所示,可见 ResNeXt 比 ResNet 以及 Inception-ResNet-v2 都要好,并且在相同计算量的情况下,错误率更低:
2. 组卷积
在讲述 ResNeXt 之前,我们首先来了解一下什么是 组卷积 (Group Convolution)。分组卷积的雏形其实可以追溯到 2012 年深度学习鼻祖文章 AlexNet。受限于当时硬件的限制,作者不得不将卷积操作拆分到两台GPU上运行,这两台GPU的参数是不共享的。后来在实现中被我们简化到一个卷积层,不分组了。
对于普通卷积而言,每个卷积核的 channel 于输入通道数保持一致。然后 $n$ 个卷积核对应于输出通道为 $n$。所以整个卷积层的参数(不考虑偏置)为 $k \times k \times C_{in} \times n$,其中 $k$ 为卷积核大小。然而对于组卷积而言,假设平均分为 $g$ 组,对每组分别进行卷积操作,每组得到的最终输出为 $n / g$。那么这 $g$ 组卷积的总参数量为 $(k \times k \times \frac{C_{in}}{g} \times \frac{n}{g}) \times g = k \times k \times C_{in} \times n / g$。即为原来的 $1/g$。如果 $g = C_{in}, n = C_{in}$ ,那么就是 DW Conv(mobileNet 会讲解),也就是对于我们输入的特征矩阵的每一个 Channel 分配了一个 Channel 为 1 的卷积核进行卷积。
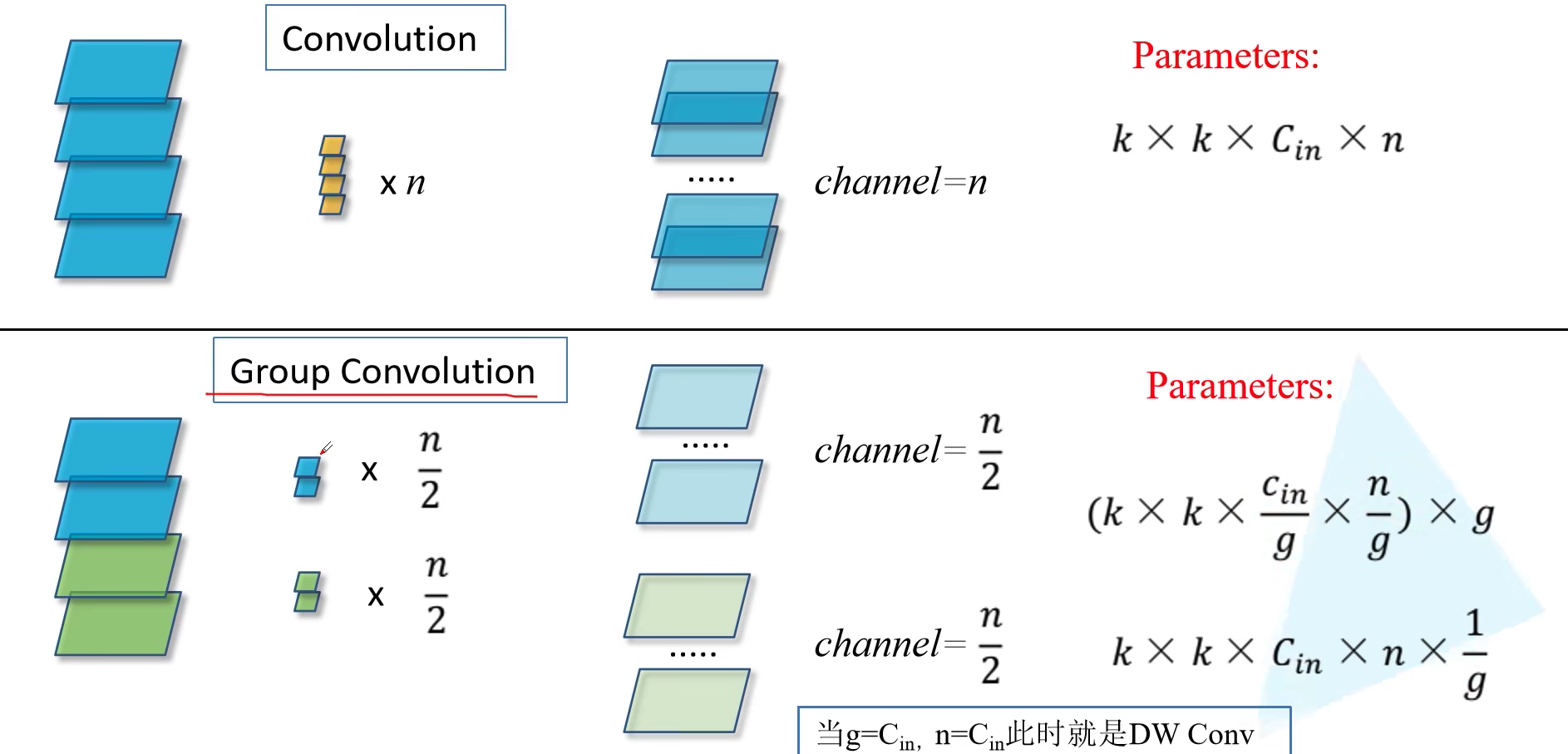
感觉什么东西,考虑居中方案,都能发文章…. 分组卷积是介于普通卷积核深度可分离卷积的一种折中方案,不是彻底的将每个 channel 都要单独赋予一个独立的卷积核,也不是整个 Feature Map 使用同一个卷积核。这就像之前说的 Group Normalization 一样….
3. ResNeXt block 分析
作者在论文中给出了三种 block 模块,注意,他们在数学计算上完全等价!其中 (c) 形式就是利用组卷积。
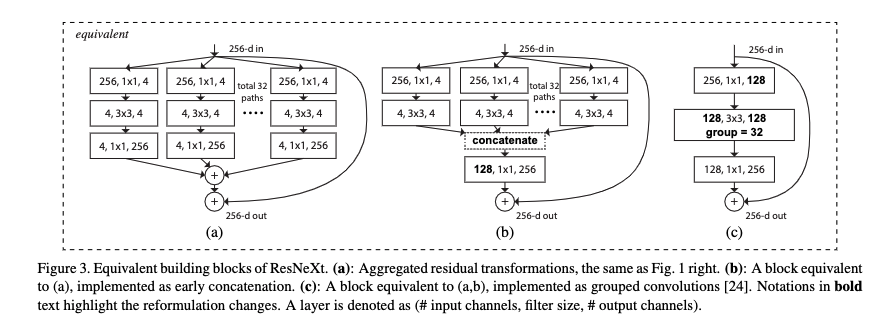
让我们来分析下为什么他们是完全等价的。
首先看从 ( c ) 到 ( b )。在 ( c ) 中上面 256 通道特征图通过 $1 \times 1$ 卷积变为 128 个通道,每个卷积核大小为 $1 \times 1 \times 256$,一共 128 个卷积核。我们考虑将 128 个卷积核 4 个一组,那么就可以成为 32 组。因为卷积核之间是没什么关联的,所以完全可以独立分开,就对应于 ( b ) 的第一行。因为在 ( c ) 中第二行是组卷积,其实也是把 $1 \times 1$ 卷积变为 128 个通道独立拆分为 32 组,每组 4 通道,就和 ( b ) 中第二层的输入是一致的。 ( b ) 的第二层其实就是把组卷积给画开了而已。所以 ( b ) 的第二层与 ( c ) 的第二层一致,即 ( b ) 和 ( c ) 是完全等价的。
然后我们看从 ( b ) 到 ( a )。重点在于为什么 concatenate 之后通过 256 个 $1 \times 1 \times 128$ 卷积和直接使用 32 组 256 个 $1 \times 1 \times 4$ 卷积后直接相加是等价的。其实这非常自然,让我们想象一下,最终输出的某个通道的某个元素,其实就是之前 128 个通道那个元素位置元素的加权求和,权就是 $1 \times 1 \times 128$ 卷积核的参数。那么他可以把 128 个求和元素拆开成先加 4 个,再加 4 个,这样加 32 下,最后再把这 32 个元素加起来。本质就是 256 个 $1 \times 1 \times 128$ 卷积核可以拆成 32 组 256 个 $1 \times 1 \times 4$ 卷积核。所以 ( b ) 和 ( a ) 是等价的。
所以为了搭建 ResNeXt 网络,只需简单地将搭建 ResNet 网络中的 block 进行替换就行了。
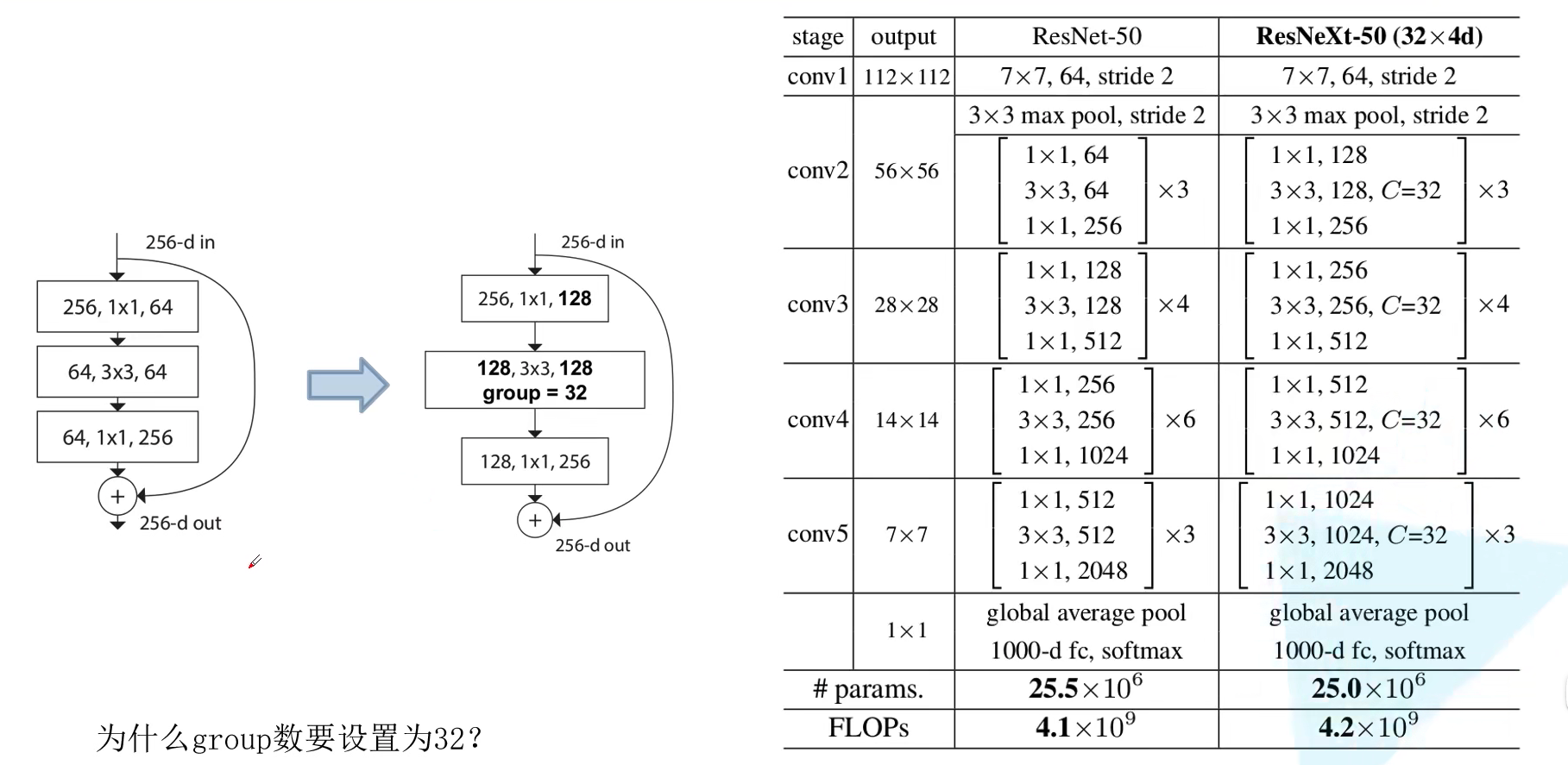
还有一个问题是:为什么要设置成 32 组?基于组数 (作者取名为 Cardinality),可以计算出组卷积通道数,使得和原始 ResNet 计算量基本一致(原论文提到尽可能减少训练过程中超参数个数)。参数量计算很简单,参考如下公式,当 $C = 32, d = 4$ 时计算可得参数量为 70k:
\[C \times (256 \times d + 3 \times 3 \times d \times d + d \times 256)\]实践是检验真理的唯一标准,在没有理论的支撑下,作者干脆就是根据实验发现,这样性能好,所以设置为 32。
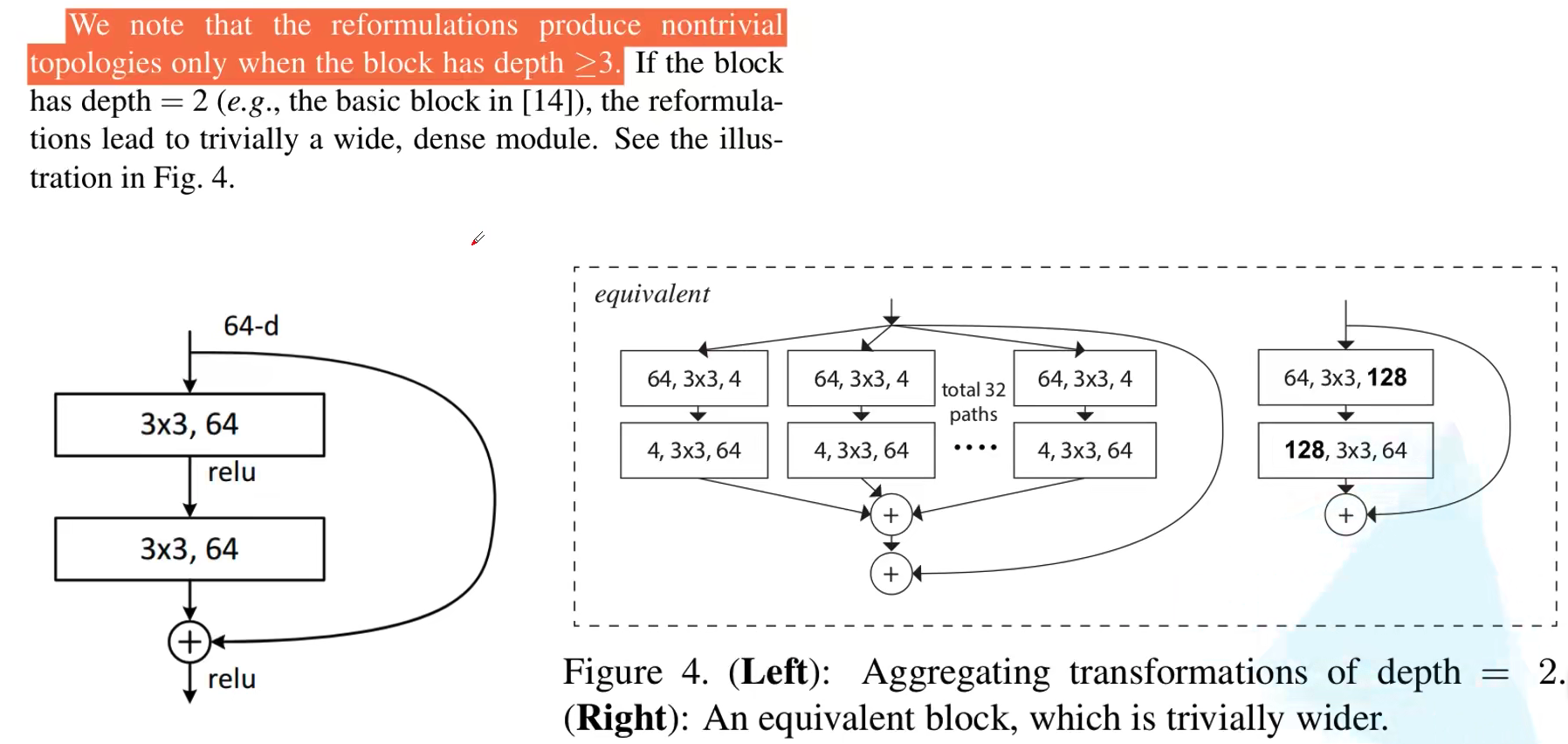
最后补充一下,上述 block 都是针对 ResNet50 及以上的网络进行替换的。如果对于浅层的例如 ResNet18 和 ResNet34 怎么替换呢?可以参考下图的结构进行替换即可。
4. 代码
注意 Bottleneck 的 groups=1, width_per_group=64 参数。观察代码,其实就是使用组卷积实现的。由此可见,如何将一件简单的事情(idea)讲成一个故事,是一门艺术!
import torch.nn as nn
import torch
class Bottleneck(nn.Module):
"""
注意:原论文中,在虚线残差结构的主分支上,第一个1x1卷积层的步距是2,第二个3x3卷积层步距是1。
但在pytorch官方实现过程中是第一个1x1卷积层的步距是1,第二个3x3卷积层步距是2,
这么做的好处是能够在top1上提升大概0.5%的准确率。
可参考Resnet v1.5 https://ngc.nvidia.com/catalog/model-scripts/nvidia:resnet_50_v1_5_for_pytorch
"""
expansion = 4
def __init__(self, in_channel, out_channel, stride=1, downsample=None,
groups=1, width_per_group=64):
super(Bottleneck, self).__init__()
width = int(out_channel * (width_per_group / 64.)) * groups
self.conv1 = nn.Conv2d(in_channels=in_channel, out_channels=width,
kernel_size=1, stride=1, bias=False) # squeeze channels
self.bn1 = nn.BatchNorm2d(width)
# -----------------------------------------
self.conv2 = nn.Conv2d(in_channels=width, out_channels=width, groups=groups,
kernel_size=3, stride=stride, bias=False, padding=1)
self.bn2 = nn.BatchNorm2d(width)
# -----------------------------------------
self.conv3 = nn.Conv2d(in_channels=width, out_channels=out_channel*self.expansion,
kernel_size=1, stride=1, bias=False) # unsqueeze channels
self.bn3 = nn.BatchNorm2d(out_channel*self.expansion)
self.relu = nn.ReLU(inplace=True)
self.downsample = downsample
def forward(self, x):
identity = x
if self.downsample is not None:
identity = self.downsample(x)
out = self.conv1(x)
out = self.bn1(out)
out = self.relu(out)
out = self.conv2(out)
out = self.bn2(out)
out = self.relu(out)
out = self.conv3(out)
out = self.bn3(out)
out += identity
out = self.relu(out)
return out
class ResNet(nn.Module):
def __init__(self,
block,
blocks_num,
num_classes=1000,
include_top=True,
groups=1,
width_per_group=64):
super(ResNet, self).__init__()
self.include_top = include_top
self.in_channel = 64
self.groups = groups
self.width_per_group = width_per_group
self.conv1 = nn.Conv2d(3, self.in_channel, kernel_size=7, stride=2,
padding=3, bias=False)
self.bn1 = nn.BatchNorm2d(self.in_channel)
self.relu = nn.ReLU(inplace=True)
self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
self.layer1 = self._make_layer(block, 64, blocks_num[0])
self.layer2 = self._make_layer(block, 128, blocks_num[1], stride=2)
self.layer3 = self._make_layer(block, 256, blocks_num[2], stride=2)
self.layer4 = self._make_layer(block, 512, blocks_num[3], stride=2)
if self.include_top:
self.avgpool = nn.AdaptiveAvgPool2d((1, 1)) # output size = (1, 1)
self.fc = nn.Linear(512 * block.expansion, num_classes)
for m in self.modules():
if isinstance(m, nn.Conv2d):
nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
def _make_layer(self, block, channel, block_num, stride=1):
downsample = None
if stride != 1 or self.in_channel != channel * block.expansion:
downsample = nn.Sequential(
nn.Conv2d(self.in_channel, channel * block.expansion, kernel_size=1, stride=stride, bias=False),
nn.BatchNorm2d(channel * block.expansion))
layers = []
layers.append(block(self.in_channel,
channel,
downsample=downsample,
stride=stride,
groups=self.groups,
width_per_group=self.width_per_group))
self.in_channel = channel * block.expansion
for _ in range(1, block_num):
layers.append(block(self.in_channel,
channel,
groups=self.groups,
width_per_group=self.width_per_group))
return nn.Sequential(*layers)
def forward(self, x):
x = self.conv1(x)
x = self.bn1(x)
x = self.relu(x)
x = self.maxpool(x)
x = self.layer1(x)
x = self.layer2(x)
x = self.layer3(x)
x = self.layer4(x)
if self.include_top:
x = self.avgpool(x)
x = torch.flatten(x, 1)
x = self.fc(x)
return x
def resnext50_32x4d(num_classes=1000, include_top=True):
# https://download.pytorch.org/models/resnext50_32x4d-7cdf4587.pth
groups = 32
width_per_group = 4
return ResNet(Bottleneck, [3, 4, 6, 3],
num_classes=num_classes,
include_top=include_top,
groups=groups,
width_per_group=width_per_group)
def resnext101_32x8d(num_classes=1000, include_top=True):
# https://download.pytorch.org/models/resnext101_32x8d-8ba56ff5.pth
groups = 32
width_per_group = 8
return ResNet(Bottleneck, [3, 4, 23, 3],
num_classes=num_classes,
include_top=include_top,
groups=groups,
width_per_group=width_per_group)
