深度学习之图像分类(五)GoogLeNet网络结构
本节学习 GoogLeNet 网络结构,学习视频源于 Bilibili,部分描述参考 大话CNN经典模型:GoogLeNet(从Inception v1到v4的演进)。

1. 前言
GoogLeNet 是 2014 年由 Google 团队提出的,斩获了当年 ImageNet 竞赛中 Classification Task 的第一名。注意是 GoogLeNet,大写 L 是为了致敬 LeNet。其原始论文为《Going deeper with convolutions》。
如何提升网络性能?一般来说,提升网络性能最直接的办法就是增加网络深度和宽度,深度指网络层次数量、宽度指神经元数量。但这种方式存在以下问题:
(1)参数太多,如果训练数据集有限,很容易产生过拟合;
(2)网络越大、参数越多,计算复杂度越大,难以应用;
(3)网络越深,容易出现梯度弥散问题(梯度越往后穿越容易消失),难以优化模型。
解决这些问题的方法当然就是在增加网络深度和宽度的同时减少参数,为了减少参数,自然就想到将全连接变成稀疏连接。但是在实现上,全连接变成稀疏连接后实际计算量并不会有质的提升,因为大部分硬件是针对密集矩阵计算优化的,稀疏矩阵虽然数据量少,但是计算所消耗的时间却很难减少。
那么,有没有一种方法既能保持网络结构的稀疏性,又能利用密集矩阵的高计算性能。大量的文献表明可以将稀疏矩阵聚类为较为密集的子矩阵来提高计算性能,就如人类的大脑是可以看做是神经元的重复堆积,因此,GoogLeNet 团队提出了 Inception 网络结构,就是构造一种“基础神经元”结构,来搭建一个稀疏性、高计算性能的网络结构。
该网络的亮点包括:
- 引入了 Inception 结构,融合不同尺度的特征信息
- 使用 $1 \times 1$ 的卷积核进行降维以及映射处理(VGGNet 中也有使用)
- 添加两个辅助分类器帮助训练(深监督,AlexNet和VGGNet都只有一个输出层)
- 丢弃全连接层,使用平均池化层(大大减少模型参数)
GoogLeNet 的网络结构图如下所示:
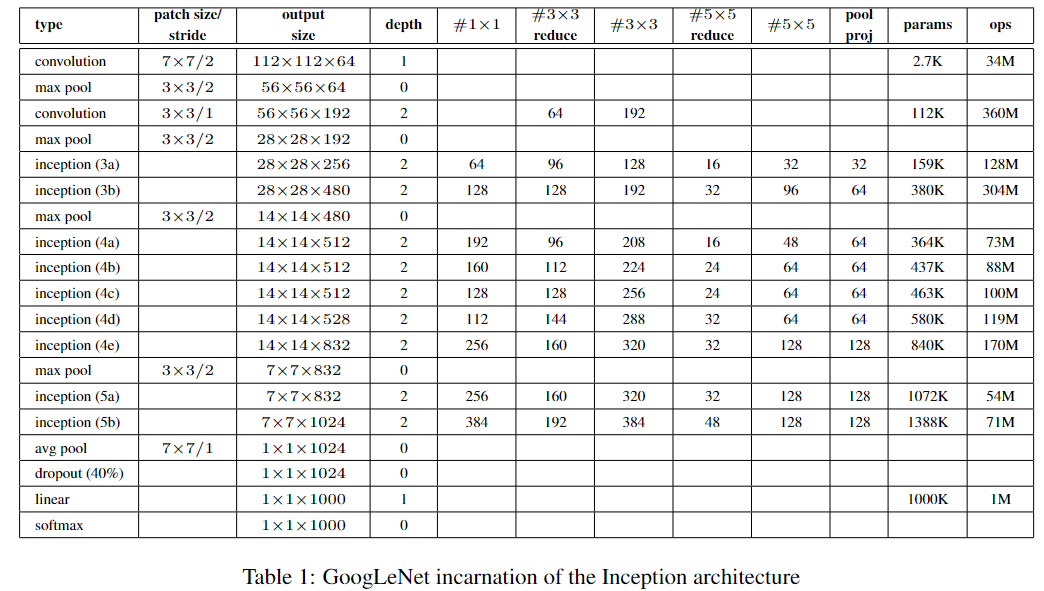
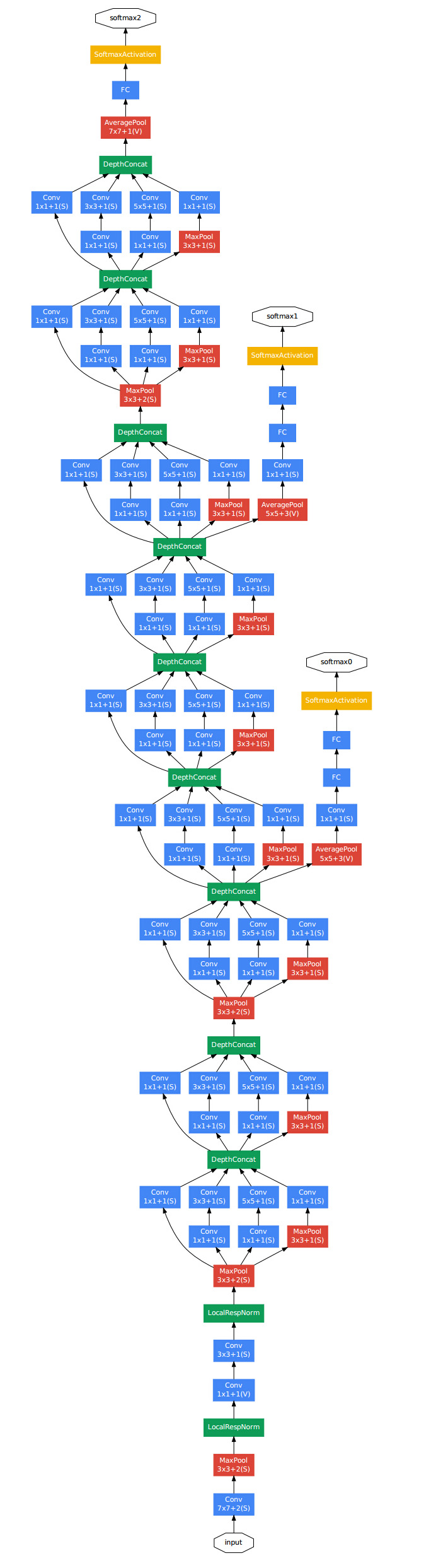
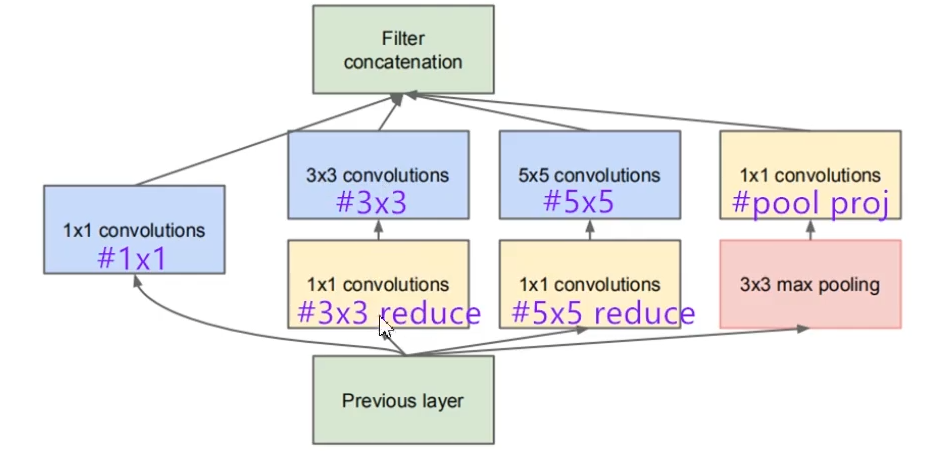
参数表中 #1x1,#3x3 reduce 等对应的子模块如下所示:
不包含辅助分类器的 GoogLeNet 的参数量约为 VGG16 的 1/20。且只相当于Alexnet的 1/12。

2. Inception 结构
在 AlexNet 和 VGGNet 中,网络都是串行结构,将一系列卷积层和池化层进行串联得到网络结构。但是在 Inception 中出现了并行结构。在图(a)中,将特征矩阵输入四个分支进行处理,再将处理结果拼接成输出特征矩阵。需要注意的是:每个分支所得到的特征矩阵的高和宽必须相同,否则我们没办法按照通道进行拼接。在图(b)中,加上了三个 $1 \times 1$ 卷积层进行降维处理。注意,在 Inception 的 Maxpool 中 stride = 1,也就是保特征图大小的池化操作。
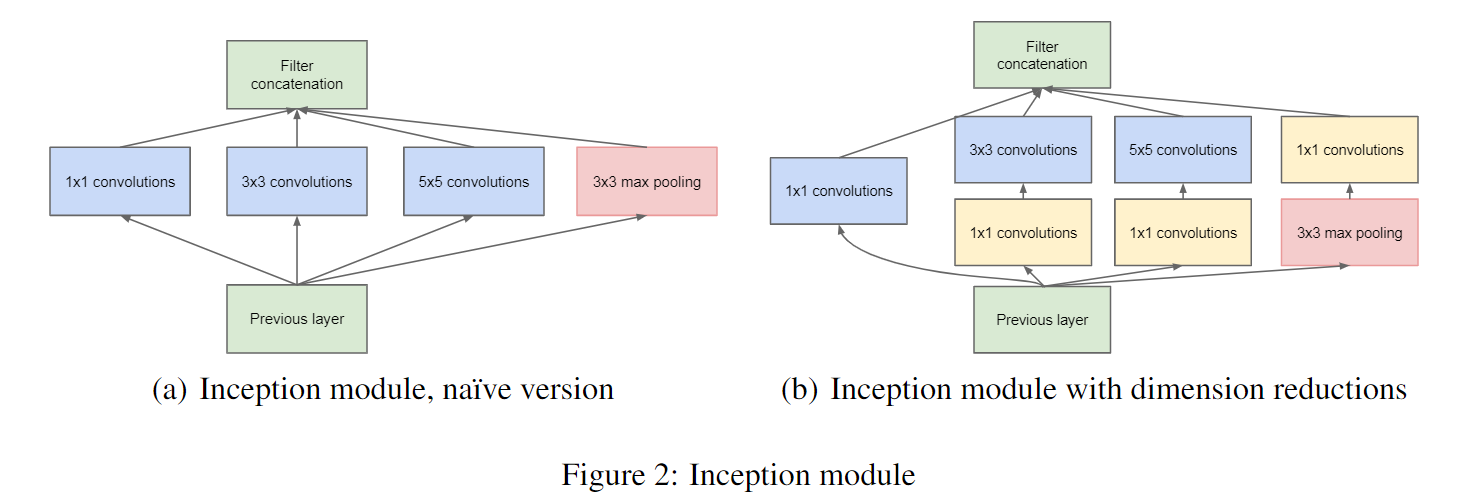
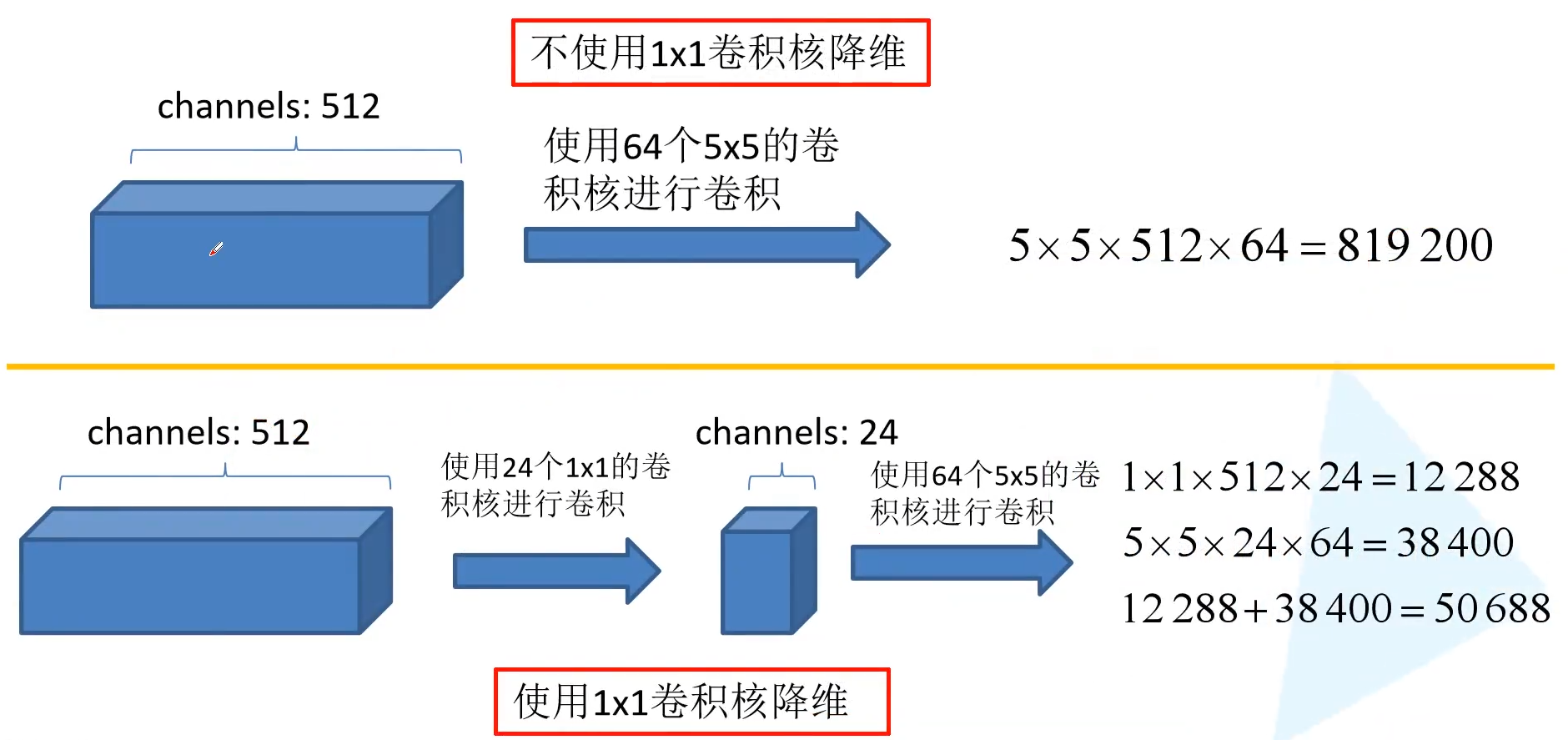
假设我们不使用 $1 \times 1$ 卷积层进行降维,对于输入通道为 512 的特征图使用 64 个 $5 \times 5$ 的卷积核进行卷积,那么参数量为 $5 \times 5 \times 512 \times 64 = 819200$。如果先使用 $1 \times 1$ 卷积将通道缩小为 24,再使用 64 个 $5 \times 5$ 的卷积核进行卷积,则参数量为 $1 \times 1 \times 512 \times 24 + 5 \times 5 \times 24 \times 64= 50688$。而且,感受野一样!
inception 有什么好处呢?Szegedy从多个角度进行了解释(参考百度百科):
解释1:在直观感觉上在多个尺度上同时进行卷积,能提取到不同尺度的特征。特征更为丰富也意味着最后分类判断时更加准确。
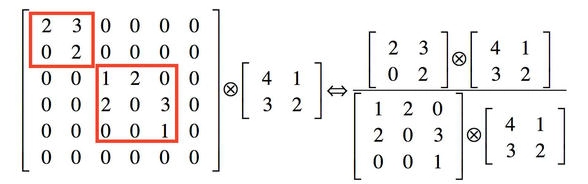
解释2:利用稀疏矩阵分解成密集矩阵计算的原理来加快收敛速度。举个例子下图左侧是个稀疏矩阵(很多元素都为 0,不均匀分布在矩阵中),和一个 2x2 的矩阵进行卷积,需要对稀疏矩阵中的每一个元素进行计算;如果像下图右图那样把稀疏矩阵分解成2个子密集矩阵,再和 2x2 矩阵进行卷积,稀疏矩阵中 0 较多的区域就可以不用计算,计算量就大大降低。这个原理应用到 inception 上就是要在特征维度上进行分解!传统的卷积层的输入数据只和一种尺度(比如 3x3 )的卷积核进行卷积,输出固定维度(比如 256 个特征)的数据,所有 256 个输出特征基本上是均匀分布在 3x3 尺度范围上,这可以理解成输出了一个稀疏分布的特征集;而 inception 模块在多个尺度上提取特征(比如 1x1,3x3,5x5 ),输出的 256 个特征就不再是均匀分布,而是相关性强的特征聚集在一起(比如 1x1 的 96 个特征聚集在一起,3x3 的 96 个特征聚集在一起,5x5 的 64 个特征聚集在一起),这可以理解成多个密集分布的子特征集。这样的特征集中因为相关性较强的特征聚集在了一起,不相关的非关键特征就被弱化,同样是输出 256 个特征,Inception 方法输出的特征“冗余”的信息较少。用这样的“纯”的特征集层层传递最后作为反向计算的输入,自然收敛的速度更快。
解释3:Hebbin 赫布原理。Hebbin 原理是神经科学上的一个理论,解释了在学习的过程中脑中的神经元所发生的变化,用一句话概括就是 fire togethter, wire together 。赫布认为 “两个神经元或者神经元系统,如果总是同时兴奋,就会形成一种‘组合’,其中一个神经元的兴奋会促进另一个的兴奋”。比如狗看到肉会流口水,反复刺激后,脑中识别肉的神经元会和掌管唾液分泌的神经元会相互促进,“缠绕”在一起,以后再看到肉就会更快流出口水。用在 Inception 结构中就是要把相关性强的特征汇聚到一起。这有点类似上面的解释2,把 1x1,3x3,5x5 的特征分开。因为训练收敛的最终目的就是要提取出独立的特征,所以预先把相关性强的特征汇聚,就能起到加速收敛的作用。
3. 辅助分类器
在 GoogLeNet 中有两个结构一模一样的辅助分类器,分别对 Inception 4a 和 Inception 4d 的输出结果进行。Inception 4a 的输出尺寸为 $14 \times 14 \times 512$,Inception 4d 的输出尺寸为 $14 \times 14 \times 528$。
辅助分类器其结构如右图所示,首先经过平均池化下采样,池化核大小为 $5 \times 5$,stride = 3,padding = 0。所以对于 Inception 4a 的输出特征矩阵变为了 $4 \times 4 \times 512$;对于 Inception 4d 的输出特征矩阵变为了 $4 \times 4 \times 528$。然后通过 $1 \times 1$ 卷积降维到 128 个通道,并使用 ReLU 激活函数。展平后使用 1024 个节点的全连接层以及 ReLU 函数(对应于右图第一个 FC)。然后经过一个 0.7 dropout ratio 的 Dropout 层,防止过拟合。然后经过 1000 个节点的输出全连接层。

4. 代码
import torch.nn as nn
import torch
import torch.nn.functional as F
class GoogLeNet(nn.Module):
def __init__(self, num_classes=1000, aux_logits=True, init_weights=False):
super(GoogLeNet, self).__init__()
self.aux_logits = aux_logits
self.conv1 = BasicConv2d(3, 64, kernel_size=7, stride=2, padding=3)
self.maxpool1 = nn.MaxPool2d(3, stride=2, ceil_mode=True)
self.conv2 = BasicConv2d(64, 64, kernel_size=1)
self.conv3 = BasicConv2d(64, 192, kernel_size=3, padding=1)
self.maxpool2 = nn.MaxPool2d(3, stride=2, ceil_mode=True)
self.inception3a = Inception(192, 64, 96, 128, 16, 32, 32)
self.inception3b = Inception(256, 128, 128, 192, 32, 96, 64)
self.maxpool3 = nn.MaxPool2d(3, stride=2, ceil_mode=True)
self.inception4a = Inception(480, 192, 96, 208, 16, 48, 64)
self.inception4b = Inception(512, 160, 112, 224, 24, 64, 64)
self.inception4c = Inception(512, 128, 128, 256, 24, 64, 64)
self.inception4d = Inception(512, 112, 144, 288, 32, 64, 64)
self.inception4e = Inception(528, 256, 160, 320, 32, 128, 128)
self.maxpool4 = nn.MaxPool2d(3, stride=2, ceil_mode=True)
self.inception5a = Inception(832, 256, 160, 320, 32, 128, 128)
self.inception5b = Inception(832, 384, 192, 384, 48, 128, 128)
if self.aux_logits:
self.aux1 = InceptionAux(512, num_classes)
self.aux2 = InceptionAux(528, num_classes)
self.avgpool = nn.AdaptiveAvgPool2d((1, 1))
self.dropout = nn.Dropout(0.4)
self.fc = nn.Linear(1024, num_classes)
if init_weights:
self._initialize_weights()
def forward(self, x):
# N x 3 x 224 x 224
x = self.conv1(x)
# N x 64 x 112 x 112
x = self.maxpool1(x)
# N x 64 x 56 x 56
x = self.conv2(x)
# N x 64 x 56 x 56
x = self.conv3(x)
# N x 192 x 56 x 56
x = self.maxpool2(x)
# N x 192 x 28 x 28
x = self.inception3a(x)
# N x 256 x 28 x 28
x = self.inception3b(x)
# N x 480 x 28 x 28
x = self.maxpool3(x)
# N x 480 x 14 x 14
x = self.inception4a(x)
# N x 512 x 14 x 14
if self.training and self.aux_logits: # eval model lose this layer
aux1 = self.aux1(x)
x = self.inception4b(x)
# N x 512 x 14 x 14
x = self.inception4c(x)
# N x 512 x 14 x 14
x = self.inception4d(x)
# N x 528 x 14 x 14
if self.training and self.aux_logits: # eval model lose this layer
aux2 = self.aux2(x)
x = self.inception4e(x)
# N x 832 x 14 x 14
x = self.maxpool4(x)
# N x 832 x 7 x 7
x = self.inception5a(x)
# N x 832 x 7 x 7
x = self.inception5b(x)
# N x 1024 x 7 x 7
x = self.avgpool(x)
# N x 1024 x 1 x 1
x = torch.flatten(x, 1)
# N x 1024
x = self.dropout(x)
x = self.fc(x)
# N x 1000 (num_classes)
if self.training and self.aux_logits: # eval model lose this layer
return x, aux2, aux1
return x
def _initialize_weights(self):
for m in self.modules():
if isinstance(m, nn.Conv2d):
nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
if m.bias is not None:
nn.init.constant_(m.bias, 0)
elif isinstance(m, nn.Linear):
nn.init.normal_(m.weight, 0, 0.01)
nn.init.constant_(m.bias, 0)
class Inception(nn.Module):
def __init__(self, in_channels, ch1x1, ch3x3red, ch3x3, ch5x5red, ch5x5, pool_proj):
super(Inception, self).__init__()
self.branch1 = BasicConv2d(in_channels, ch1x1, kernel_size=1)
self.branch2 = nn.Sequential(
BasicConv2d(in_channels, ch3x3red, kernel_size=1),
BasicConv2d(ch3x3red, ch3x3, kernel_size=3, padding=1) # 保证输出大小等于输入大小
)
self.branch3 = nn.Sequential(
BasicConv2d(in_channels, ch5x5red, kernel_size=1),
BasicConv2d(ch5x5red, ch5x5, kernel_size=5, padding=2) # 保证输出大小等于输入大小
)
self.branch4 = nn.Sequential(
nn.MaxPool2d(kernel_size=3, stride=1, padding=1),
BasicConv2d(in_channels, pool_proj, kernel_size=1)
)
def forward(self, x):
branch1 = self.branch1(x)
branch2 = self.branch2(x)
branch3 = self.branch3(x)
branch4 = self.branch4(x)
outputs = [branch1, branch2, branch3, branch4]
return torch.cat(outputs, 1)
class InceptionAux(nn.Module):
def __init__(self, in_channels, num_classes):
super(InceptionAux, self).__init__()
self.averagePool = nn.AvgPool2d(kernel_size=5, stride=3)
self.conv = BasicConv2d(in_channels, 128, kernel_size=1) # output[batch, 128, 4, 4]
self.fc1 = nn.Linear(2048, 1024)
self.fc2 = nn.Linear(1024, num_classes)
def forward(self, x):
# aux1: N x 512 x 14 x 14, aux2: N x 528 x 14 x 14
x = self.averagePool(x)
# aux1: N x 512 x 4 x 4, aux2: N x 528 x 4 x 4
x = self.conv(x)
# N x 128 x 4 x 4
x = torch.flatten(x, 1)
x = F.dropout(x, 0.5, training=self.training)
# N x 2048
x = F.relu(self.fc1(x), inplace=True)
x = F.dropout(x, 0.5, training=self.training)
# N x 1024
x = self.fc2(x)
# N x num_classes
return x
class BasicConv2d(nn.Module):
def __init__(self, in_channels, out_channels, **kwargs):
super(BasicConv2d, self).__init__()
self.conv = nn.Conv2d(in_channels, out_channels, **kwargs)
self.relu = nn.ReLU(inplace=True)
def forward(self, x):
x = self.conv(x)
x = self.relu(x)
return x
