深度学习之图像分类（一）-- 分类模型的混淆矩阵

木卯 于 2021-08-26 发布

深度学习之图像分类（一）分类模型的混淆矩阵

今天开始学习深度学习图像分类模型Backbone理论知识，首先学习分类模型的混淆矩阵，学习视频源于 Bilibili。

img5

1. 混淆矩阵

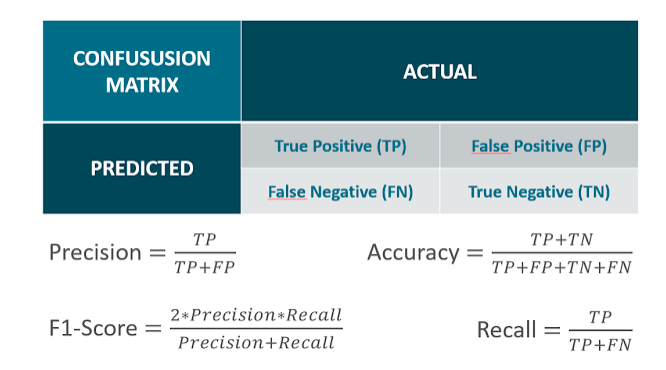
混淆矩阵是评判模型结果的一种指标，属于模型评估的一部分，常用语评判分类模型的优劣。图中左下角为混淆矩阵的一个示例，横坐标为 True Label，纵坐标为 Predicted Label。混淆矩阵每一行对应着预测属于该类的所有样本，混淆矩阵的对角线表示预测正确的样本个数。希望网络预测过程中，将预测类别分布在对角线上。预测值在对角线上分布越密集，则表现模型性能越好。通过混淆矩阵还容易看出模型对于哪些类别容易分类出错。

利用混淆矩阵可以算出精确率，召回率和特异度，这三个指标是对于每个类别得到的结果。注意到，精确率和准确率 Accuracy 是不一样的。准确率是使用所有预测正确样本的个数除以所有样本数量之和。

img0

1.1 二分类混淆矩阵

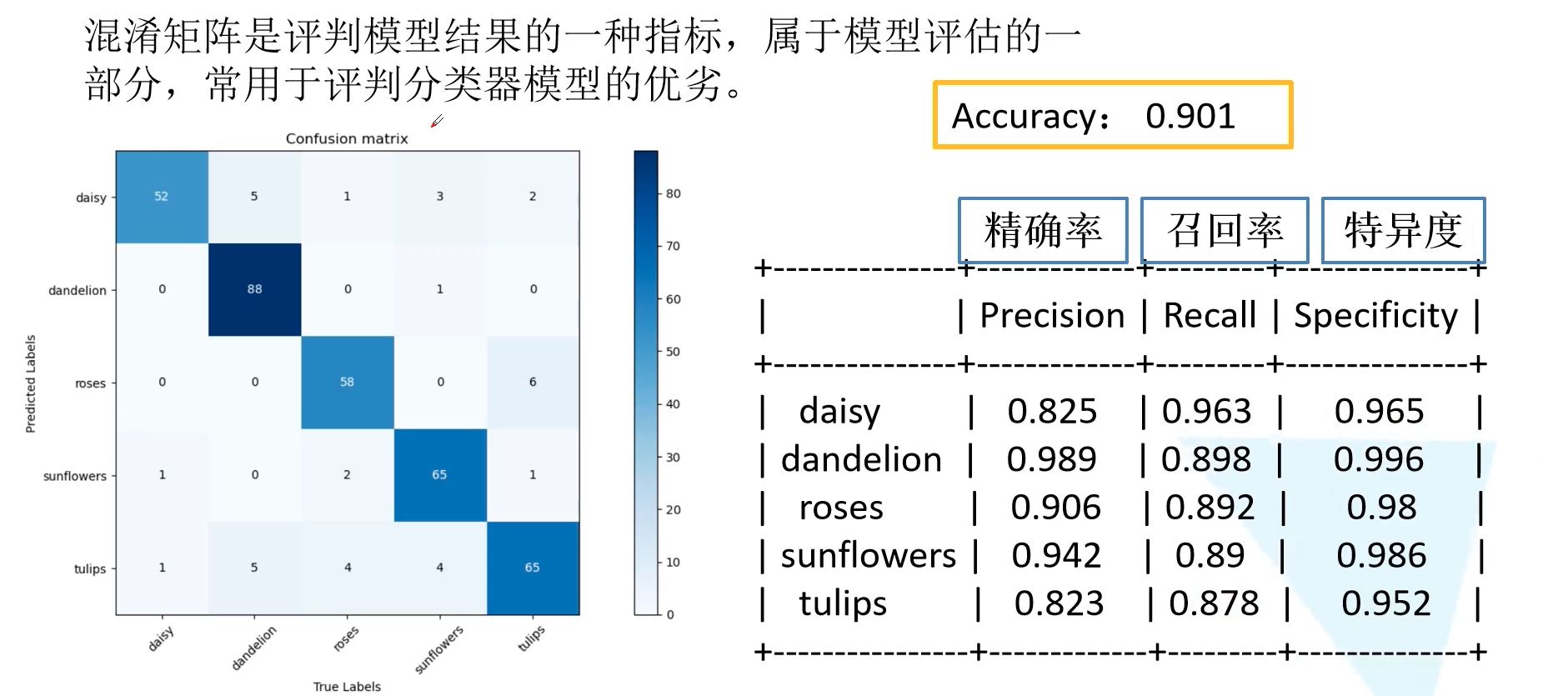
我们首先以二分类混淆矩阵作为讲解。首先每一列表示真实值的标签，每一列表示预测值的标签。Positive 为正样本，Negative 为负样本。此时我们可以有四种分类：

TP 和 TN 都对应着网络预测正确的部分，FP 和 FN 对应着网络预测错误的部分。所以我们期望 TP 和 TN 越大越好，而 FP 和 FN 越小越好。

img1

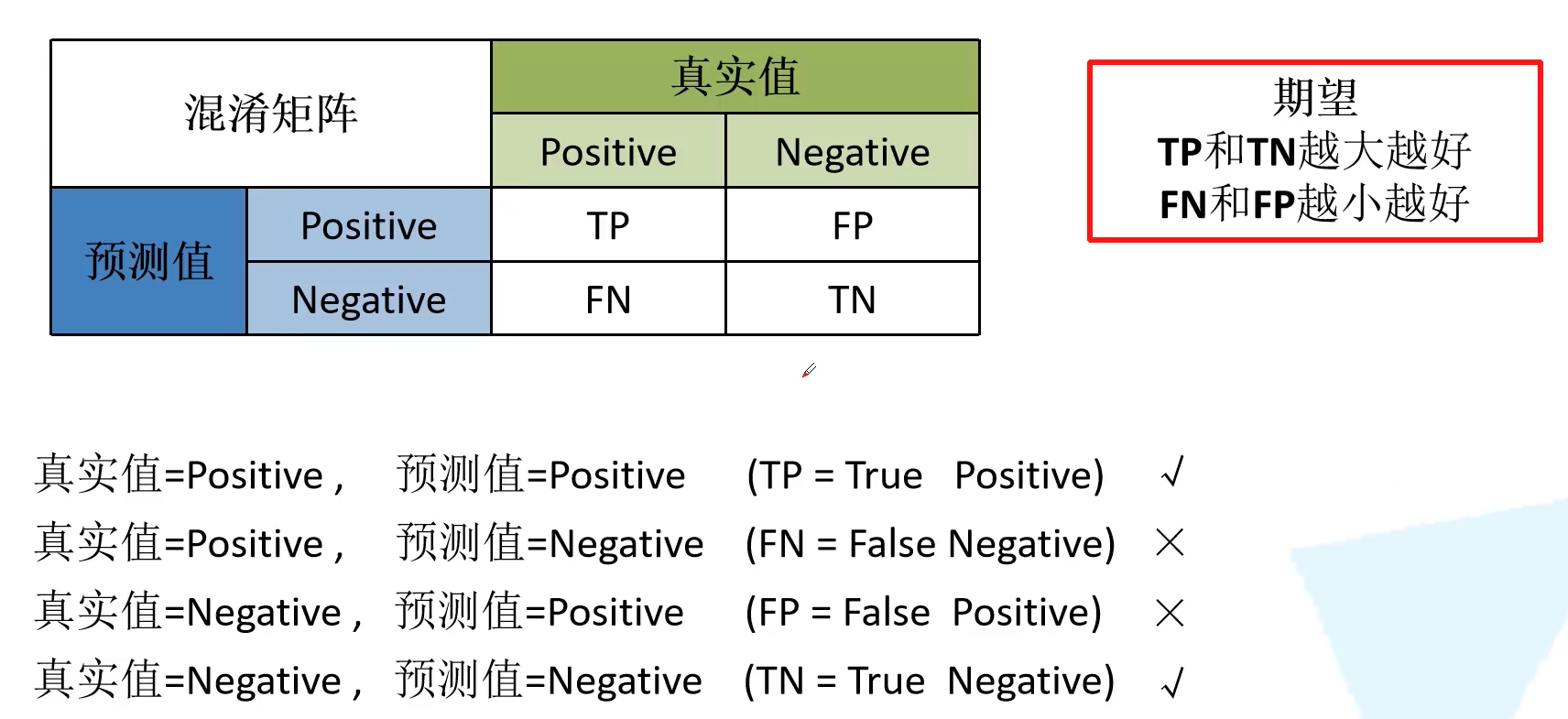
有了 TP、FN、FP、TN 的概念后，我们就可以引入准确率 (Acc, Accuracy)、精确率 (PPV, Positive Predictive Value)、召回率 (TPR, True Positive Rate) 以及特异度 (TNR, True Negative Rate)。注意到，准确率是对所有样本而言的，精确率召回率以及特异度是对于每个类别而言的。计算公式如下表所示：

img2

1.2 混淆矩阵计算实例

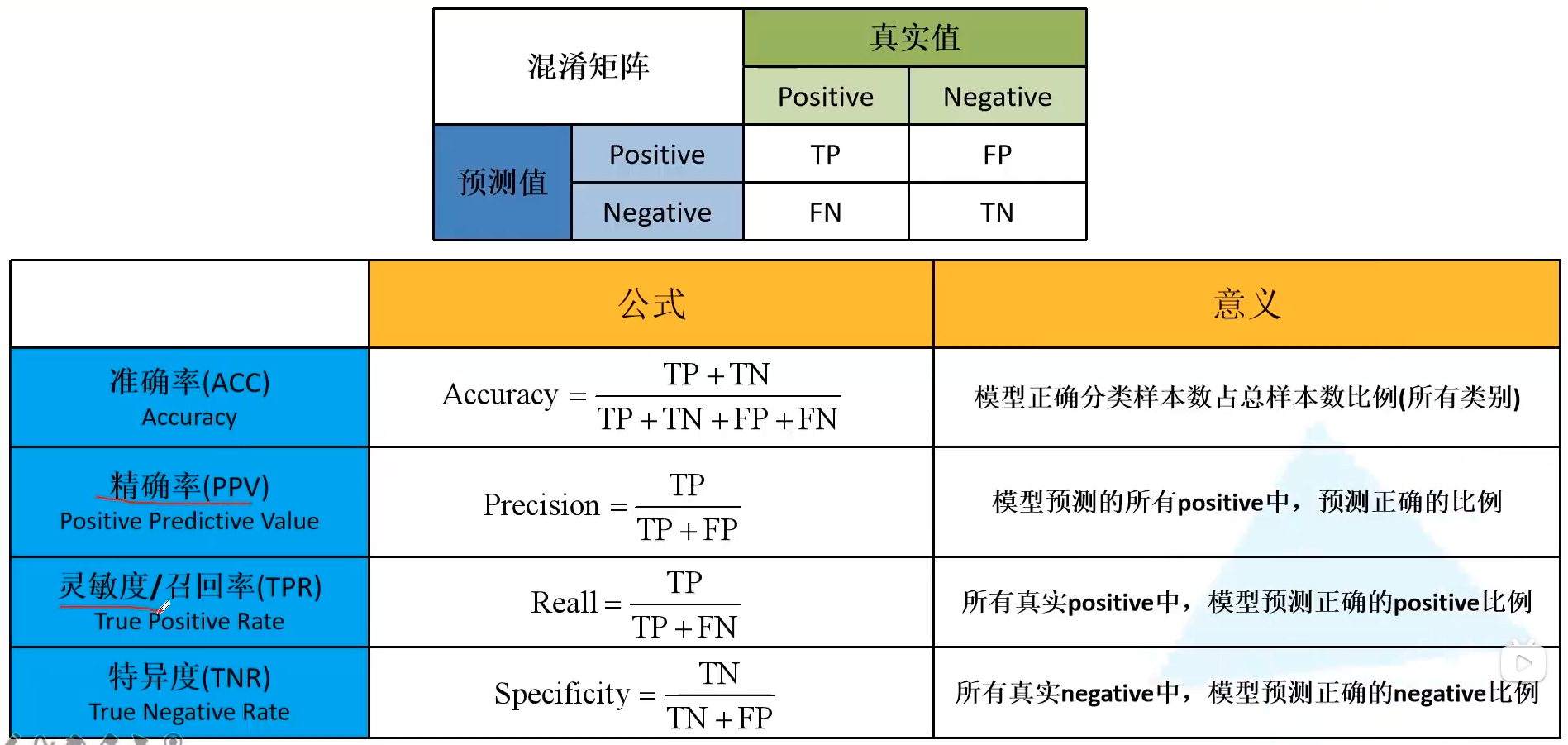
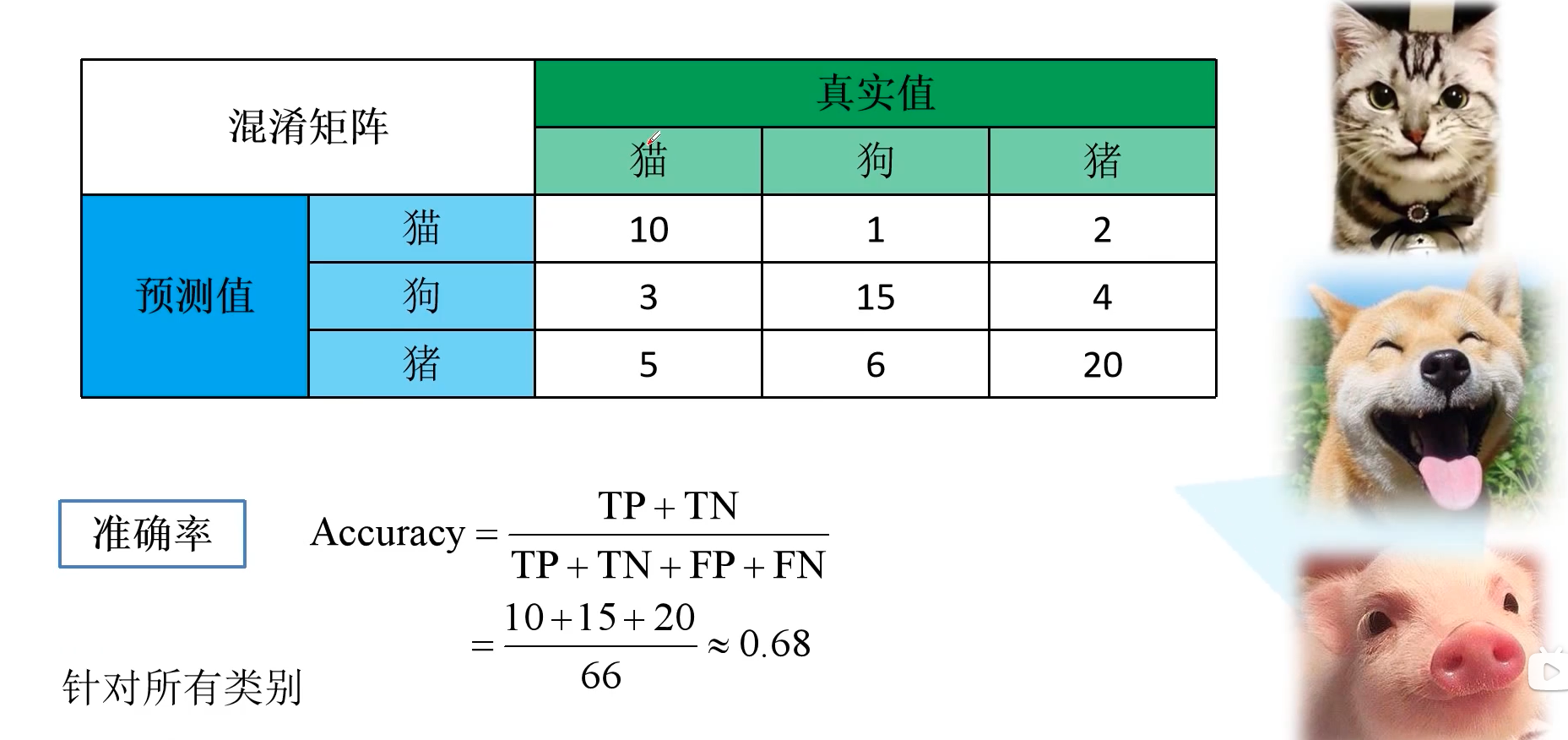
下图给出了一个计算指标的实例，以猫狗猪三分类为例。准确率计算结果如下所示：

img3

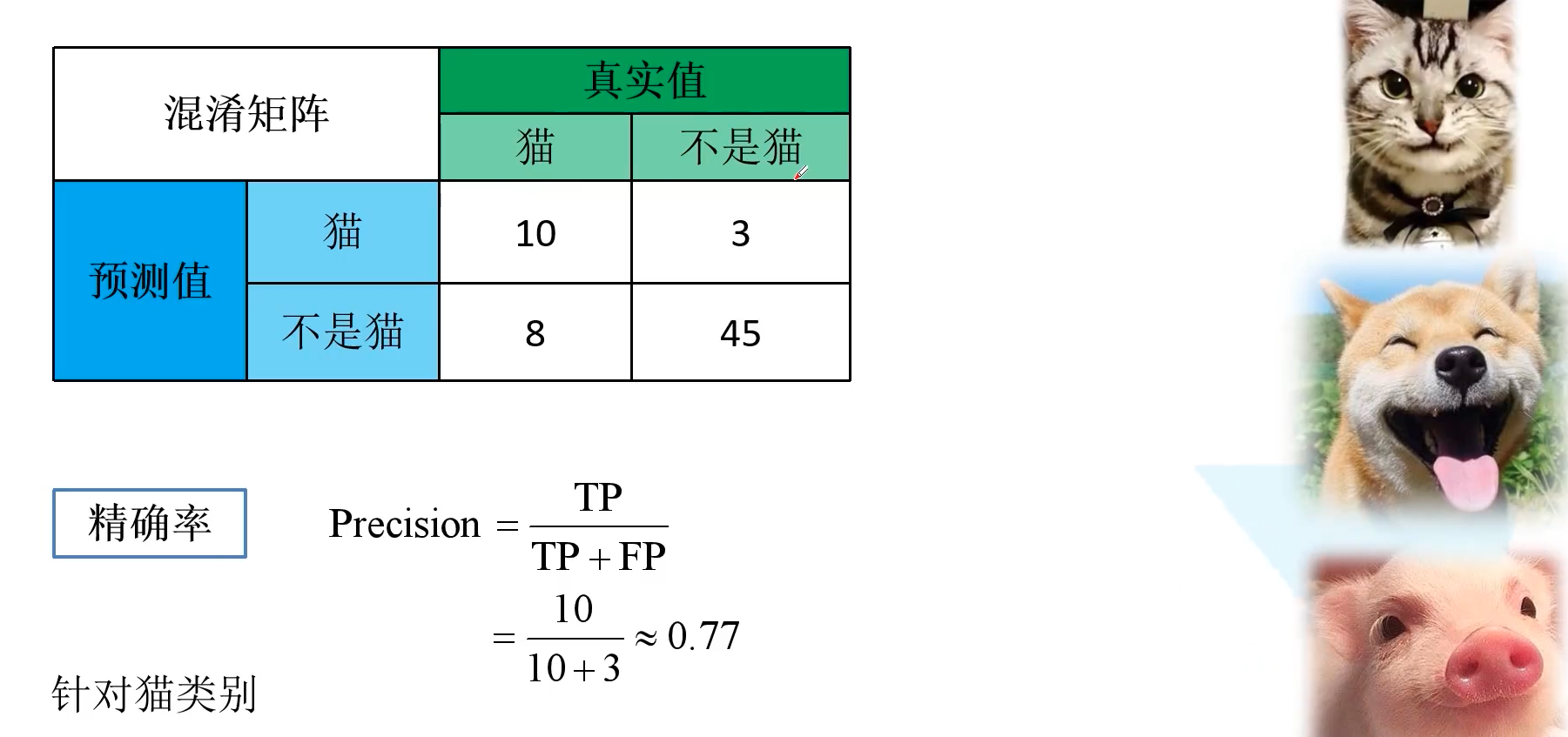
为了算针对 猫 类别的精确率召回率以及特异度，我们统一将狗和猪融合为不为猫的情况。精确率 Precision = 10 / (10 + 3) = 0.77，同样的能算出召回率 Recall = 10 / (10 + 8) = 0.56，特异度 Sepcificity = 45 / (45 + 3) = 0.94。

img4

2. 混淆矩阵代码

完整代码详见 此处。

import os
import json

import torch
from torchvision import transforms, datasets
import numpy as np				# 用 numpy 实现，目的是 pytorch 和 tensorflow 的框架都能使用，label.numpy()
from tqdm import tqdm
import matplotlib.pyplot as plt
from prettytable import PrettyTable

class ConfusionMatrix(object):
    """
    注意，如果显示的图像不全，是matplotlib版本问题
    本例程使用matplotlib-3.2.1(windows and ubuntu)绘制正常
    需要额外安装prettytable库: pip install prettytable
    """
    def __init__(self, num_classes: int, labels: list):
        self.matrix = np.zeros((num_classes, num_classes))	# 初始化混淆矩阵
        self.num_classes = num_classes
        self.labels = labels

    # 混淆矩阵更新
    def update(self, preds, labels):
        for p, t in zip(preds, labels):
            self.matrix[p, t] += 1

    # 计算并打印评价指标
    def summary(self):
        # calculate accuracy
        sum_TP = 0
        for i in range(self.num_classes):
            sum_TP += self.matrix[i, i]				# 对角线元素求和
        acc = sum_TP / np.sum(self.matrix)
        print("the model accuracy is ", acc)

        # precision, recall, specificity
        table = PrettyTable()
        table.field_names = ["", "Precision", "Recall", "Specificity"]	# 第一个元素是类别标签
        for i in range(self.num_classes):			# 针对每个类别进行计算
            # 整合其他行列为不属于该类的情况
            TP = self.matrix[i, i]
            FP = np.sum(self.matrix[i, :]) - TP
            FN = np.sum(self.matrix[:, i]) - TP
            TN = np.sum(self.matrix) - TP - FP - FN
            Precision = round(TP / (TP + FP), 3) if TP + FP != 0 else 0.		# 注意分母为 0 的情况
            Recall = round(TP / (TP + FN), 3) if TP + FN != 0 else 0.
            Specificity = round(TN / (TN + FP), 3) if TN + FP != 0 else 0.
            table.add_row([self.labels[i], Precision, Recall, Specificity])
        print(table)

    # 可视化混淆矩阵
    def plot(self):
        matrix = self.matrix
        print(matrix)
        plt.imshow(matrix, cmap=plt.cm.Blues)		# 从白色到蓝色

        # 设置x轴坐标label
        plt.xticks(range(self.num_classes), self.labels, rotation=45)	# x 轴标签旋转 45 度方便展示
        # 设置y轴坐标label
        plt.yticks(range(self.num_classes), self.labels)
        # 显示colorbar
        plt.colorbar()
        plt.xlabel('True Labels')
        plt.ylabel('Predicted Labels')
        plt.title('Confusion matrix')

        # 在图中标注数量/概率信息
        thresh = matrix.max() / 2
        for x in range(self.num_classes):
            for y in range(self.num_classes):
                # 注意这里的matrix[y, x]不是matrix[x, y]
                # 画图的时候横坐标是x，纵坐标是y
                info = int(matrix[y, x])
                plt.text(x, y, info,
                         verticalalignment='center',
                         horizontalalignment='center',
                         color="white" if info > thresh else "black")
        plt.tight_layout()		# 图形显示更加紧凑
        plt.show()

3. 混淆矩阵用途