深度学习之目标检测（八）-- YOLOv3理论介绍

木卯 于 2021-08-23 发布

深度学习之目标检测（八）YOLOv3理论介绍

本章学习 YOLO v3 相关理论知识，学习视频源于 Bilibili，部分参考叙述源自 知乎 。

1. YOLO v3

YOLO v2 论文为发表于 2018 CVPR 的 YOLOv3: An Incremental Improvement。YOLOv3 更像是作者一年工作的总结，不像一篇正式的 paper，没有太多创新点，整合了当前主流网络的优点，其核心在于做大做强，再创辉煌。通过在 COCO 数据集上正确率的对比我们可以看出，相比于其他网络而言，YOLOv3 速度非常的快，但是正确率并没有那么高。

img0

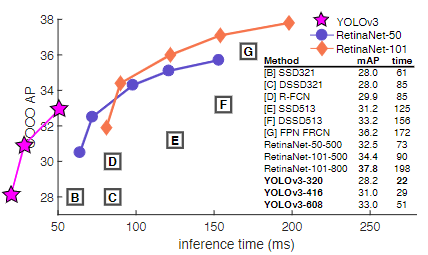
当 IoU=0.5 时候的 AP 对应的是 PASCAL VOC 的评价指标了，可见其检测效果对于其他网络而言还是有竞争力的，且速度奇快无比。

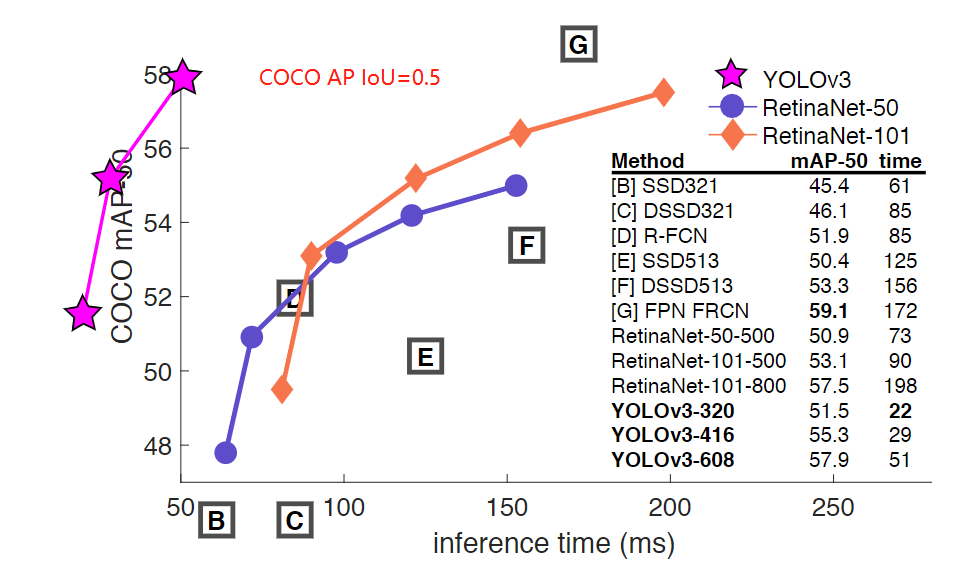
img00

1.1 YOLOv3 网络架构

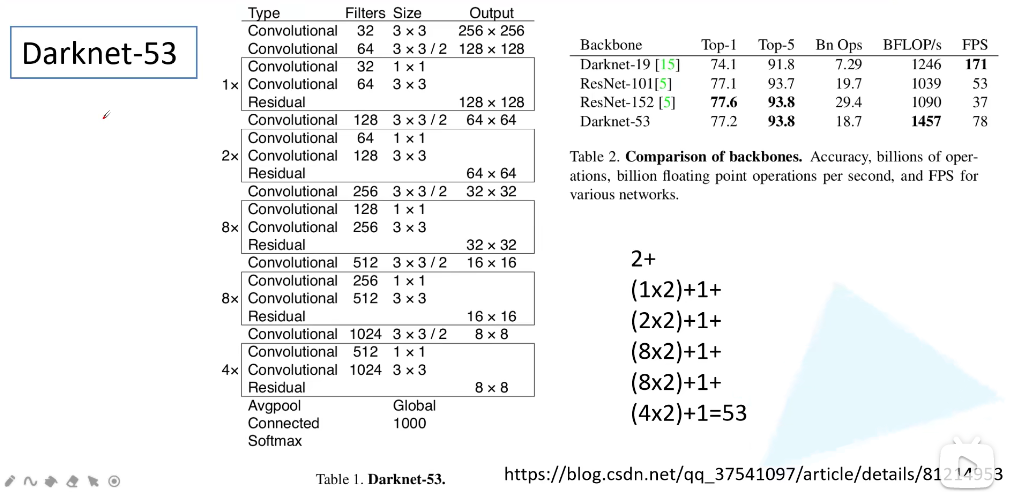
YOLOv3 的第一个改进之处就是将 backbone 替换为 Darknet-53。在 YOLOv2 中采用的是 Darknet-19 这样一个网络。Darknet-53 的 top-1 准确率相较于 Darknet-19 有比较大的提升，与 ResNet 性能相当，但是检测速度 FPS 比 ResNet 要好很多。注意最后的全连接层也是可以通过卷积来实现的，所以最后那里的 Connected 也算了一个卷积层。

img1

什么是 Top-1 和 Top-5 准确率？

模型在 ImageNet 数据集上进行推理，按照置信度排序总共生成 5 个标签。按照第一个标签预测计算正确率，即为 Top-1 正确率；前五个标签中只要有一个是正确的标签，则视为正确预测，称为 Top-5 正确率。

为什么 Darknet-53 比更深层的 ResNet 的效果要好一些呢？

通过看网络结构，和 ResNet 没有太大的区别，都是堆叠一系列的残差结构来得到最终网络的。但是细看在 Darknet-53 中是没有池化层的，所有下采样都是通过卷积层来实现的。那速度为什么这么快呢？Darknet-53 的卷积核个数（通道数）要少一些，网络计算量要少一些。 —— 个人观点仅供参考

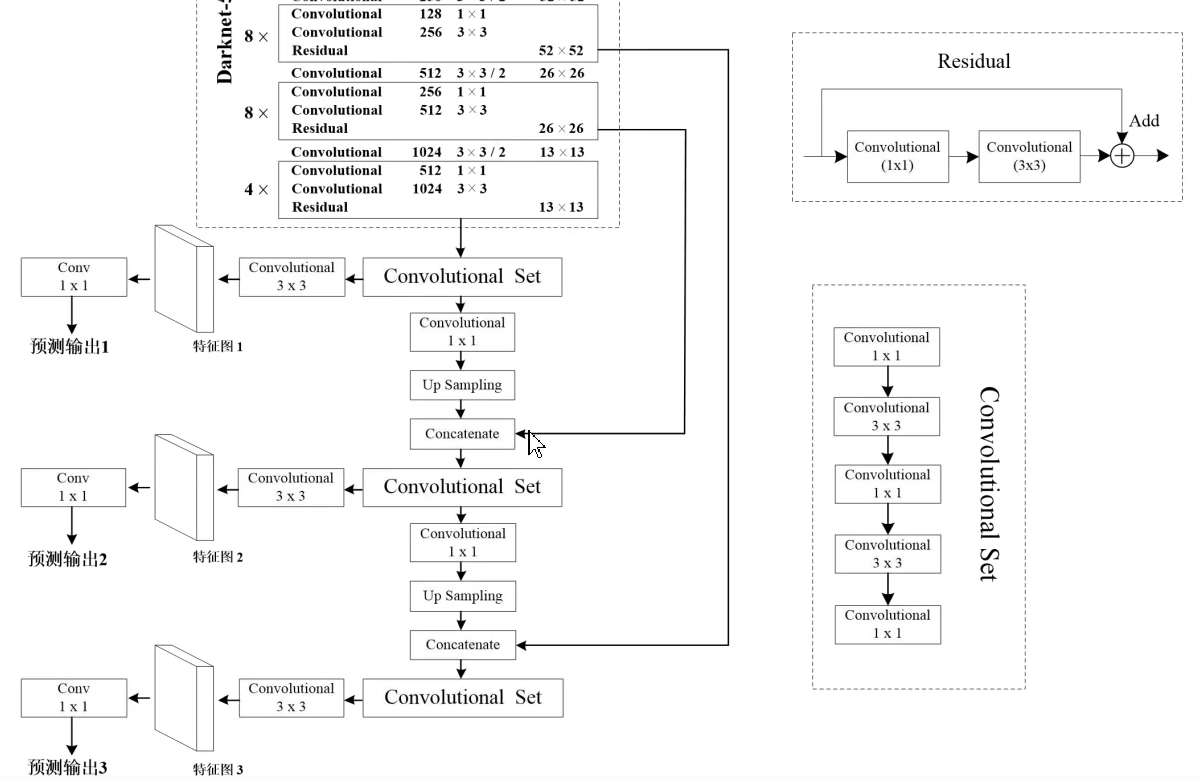
最终整体网络结构如下所示，其实一个 Convolutional 包含三个部分：卷积层，BN层和 LeakyReLU 激活层，因为使用了 BN 层（BN 操作自带偏置），所以卷积层是没有偏置 bias 的。

img2

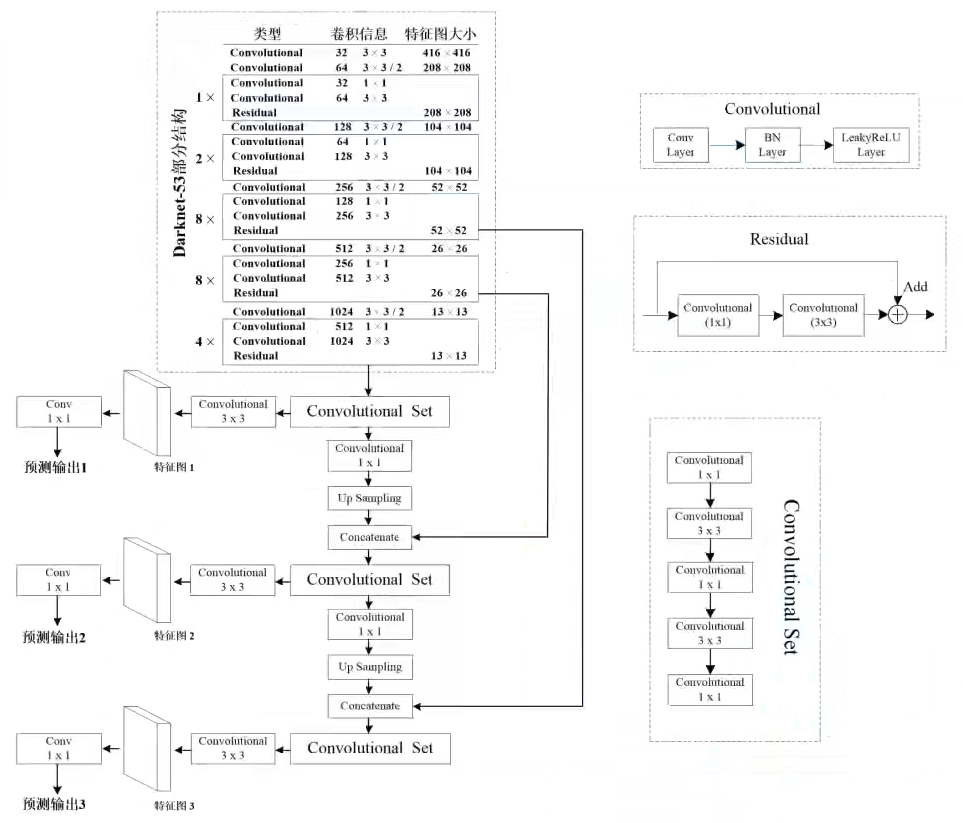
关于 YOLOv3 模型结构部分，其实原始论文讲得非常模糊，比如原始论文中说来自前面的两个层（哪两个？），来自早期的特征层（哪一个？），添加一些卷积层（在哪里添加什么样子的？）。光看论文还不够搭建出来，看源码才能看出来。YOLOv3 其实是在三个预测特征层上进行预测的，每个预测特征层上会使用三种尺度，这也是根据 K-means 算法得到的，得到的九组尺度（下图中左下角部分）三个三个一分就分给了三个预测特征层，依然保持早期特征层预测小目标，后期特征层预测大目标的做法。这些预设的框被称为 bounding box priors，这个和 Anchor 以及 Default box 其实是一个概念。

img3

img4

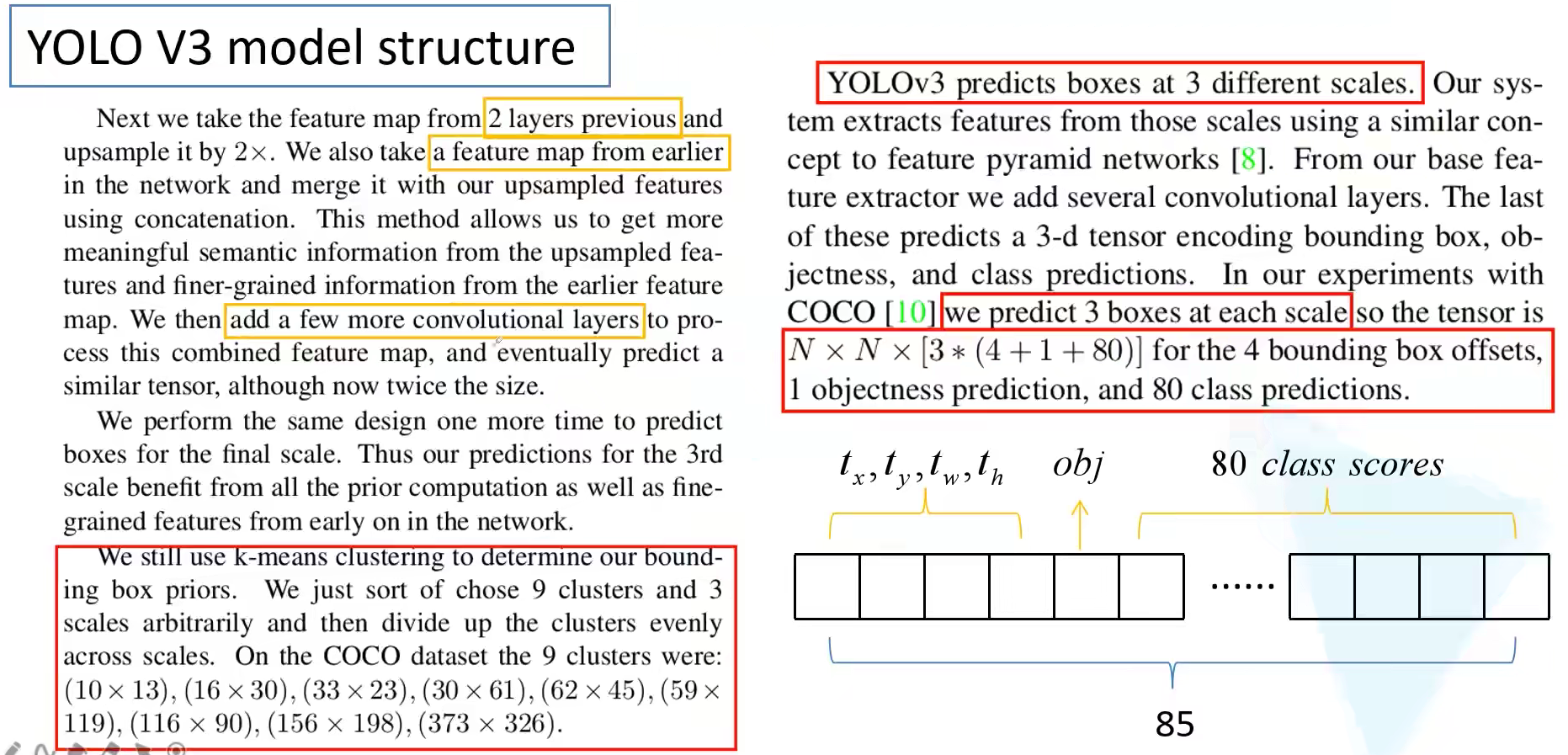
最终在COCO数据集上进行预测，在每一个预测特征层上会预测 $N \times N \times [3 * (4 + 1 + 80)]$ 个参数。

在 YOLO 中，这部分拼接 concatenate 是在通道维度上进行，回忆 FPN 则是在对应元素上做加法! 将拼接后预测特征图的进行预测。预测器 Conv $1 \times 1$ 就是一个卷积层。

img5

1.2 目标边界框预测

在 YOLOv3 中目标边界框预测和 YOLOv2 其实是一样的。并且使用 k-means 对数据集中的标签框进行聚类，得到类别中心点的 9 个框，作为先验框。在 COCO 数据集中（原始图片全部 resize 为 416 × 416），九个框分别是 (10 × 13)，(16 × 30)，(33 × 23)，(30 × 61)，(62 × 45)，(59 × 119)， (116 × 90)， (156 × 198)，(373 × 326) ，顺序为 w × h。值得注意的是，先验框只与检测框的尺寸 w、h 有关，与位置 x、y 无关。

下面这个图和原论文的图其实有一点不一样，因为原论文中写到偏移量其实是相对于 cell 的左上角位置来的，所以下面这个图的虚线框 Anchor 的中心画到了 cell 的左上角，它的中心坐标就是 $(c_x, c_y)$，宽度和高度就是 $P_w$ 和 $P_h$。预测值就是 $t_x, t_y, t_w, t_h$，$\sigma$ 是 sigmoid 函数。通过上述公式，计算出实际预测框的位置以及宽高 $(b_x, b_y, b_w, b_h)$。注意到，confidence 值也需要进行 sigmoid 函数处理归一化到 [0. 1] 中。

·img6

举个具体的例子，假设对于第二个特征图 16 × 16 × 3 × 85 中的第 [5，4，2] 维，上图中的 $c_y$ 为 5， $c_x$ 为 4，第二个特征图对应的先验框为 (30 × 61)，(62 × 45)，(59 × 119)，prior_box 的 index 为 2，那么取最后一个59 和 119 分别作为先验 $P_w$、先验 $P_h$。这样计算之后的 $b_x, b_y$ 还需要乘以特征图二的采样率 16，得到真实的检测框的 x 和 y 中心坐标位置。最后在进行裁剪确保检测框限定在目标图像内即可。

三个特征图一共可以解码出 8 × 8 × 3 + 16 × 16 × 3 + 32 × 32 × 3 = 4032 个 bounding box 以及相应的类别、置信度。这 4032 个 bounding box，在训练和推理时，使用方法不一样：

YOLOv3 不再像 YOLOv1 和 YOLOv2 那样，每个 cell 负责中心落在该 cell 中的 ground truth。原因是 YOLOv3 一共产生3 个特征图，3 个特征图上的 cell，中心是有重合的。训练时，可能最契合的是特征图 1 的第 3 个 box，但是推理的时候特征图 2 的第 1 个 box 置信度最高。所以 YOLOv3 的训练，不再按照 ground truth 中心点，严格分配指定 cell，而是根据预测值寻找 IOU 最大的预测框作为正例。

Anchor 如何和 Cell 进行匹配？比较位置偏移量是相对于 Cell 左上角而言的。知乎网友有个详细的回答：

求 IOU 和 Anchor 位置无关，只和形状有关，假设一共有 9 种 Anchor，那么找到和 GT 重合最大的那个 Anchor，假设这个 Anchor 属于最后一层 feature map 的第一种 Anchor 形状上，那么然后算出 GT 的中心点落在最后一层 feature map 的对应 cell，然后就是这个 cell 的第一种 Anchor 形状来负责预测它！

1.3 正负样本匹配

在 YOLOv3 中正负样本是如何匹配的呢？对每一个 ground box 会分配一个 bounding box prior，一张图片中有几个 GT 目标，就有几个正样本。并且将与 GT box 重合度最高（IoU 分数最大）的 bounding box prior 作为正样本。对于那些与某个 GT box 重合度超过一定阈值（论文中使用 0.5），但是又不是最大的，则它既不是正样本也不是负样本，直接将其进行丢弃不用于计算损失。对于剩下的样本（与所有 GT box 的 IoU 分数都小于 0.5）则认为是负样本。仅有正样本才有定位损失和类别损失，负样本仅仅用于计算 confidence 值损失。

img7

这里有几个注意点需要强调：

1.4 损失函数

YOLOv3 的损失依然由三部分组成，置信度损失，分类损失以及定位损失。在 YOLOv3 的原始论文中没有给出具体的损失函数公式。

img8

特征图 1 的 Yolov3 的损失函数抽象表达式如下： \(\begin{gathered} \operatorname{los} s_{N_{1}}=\lambda_{b o x} \sum_{i=0}^{N_{1} \times N_{1}} \sum_{j=0}^{3} 1_{i j}^{o b j}\left[\left(t_{x}-t_{x}^{\prime}\right)^{2}+\left(t_{y}-t_{y}^{\prime}\right)^{2}\right] \\ +\lambda_{b o x} \sum_{i=0}^{N_{1} \times N_{1}} \sum_{j=0}^{3} 1_{i j}^{o b j}\left[\left(t_{w}-t_{w}^{\prime}\right)^{2}+\left(t_{h}-t_{h}^{\prime}\right)^{2}\right] \\ -\lambda_{o b j} \sum_{i=0}^{N \times N} \sum_{j=0}^{3} 1_{i j}^{o b j} \log \left(c_{i j}\right) \\ -\lambda_{\text {noobj }} \sum_{i=0}^{N_{1} \times N_{1}} \sum_{j=0}^{3} 1_{i j}^{n o o b j} \log \left(1-c_{i j}\right) \\ \qquad-\lambda_{\text {class }} \sum_{i=0}^{N_{1} \times N_{1}} \sum_{j=0}^{3} 1_{i j}^{o b j} \sum_{c \in \text { classes }}\left[p_{i j}^{\prime}(c) \log \left(p_{i j}(c)\right)+\left(1-p_{i j}^{\prime}(c)\right) \log \left(1-p_{i j}(c)\right)\right] \end{gathered}\) $\lambda$ 为权重常数，控制检测框 Loss、obj 置信度 Loss、noobj 置信度 Loss 之间的比例，通常负例的个数是正例的几十倍以上，可以通过权重超参控制检测效果。$1{ij}^{obj}$ 若是正例则输出 1，否则为0；$1{ij}^{noobj}$ 若是负例则输出 1，否则为 0；忽略样例都输出 0。看着复杂不要怕，我们来一个一个分析：

1.4.1 置信度损失

首先是置信度损失，右下角原文写了，对于所有 bounding box 的置信度分数使用逻辑回归，网上一般使用逻辑回归都是使用二值交叉熵损失，包括源码也是使用的二值交叉熵损失。在原文中其实只有 0 和 1 两个值的。但是在 YOLOv3+SPP （下篇博客会讲）中，置信度损失计算部分求得的 $o_i$ 就是预测目标边界框与真实目标边界框的 IoU 值（注意不是 bounding box prior 和 GT box）。假设右边蓝色的部分是 bounding box prior，绿色边界框是 GT box，黄色就是预测的 4 个边界框回归参数作用于蓝色的 bounding box prior 得到预测目标边界框。黄色和绿色的边界框的 IoU 就是 $o_i$ 了。嫌麻烦其实可以直接取 0 和 1。

img9

1.4.2 类别损失

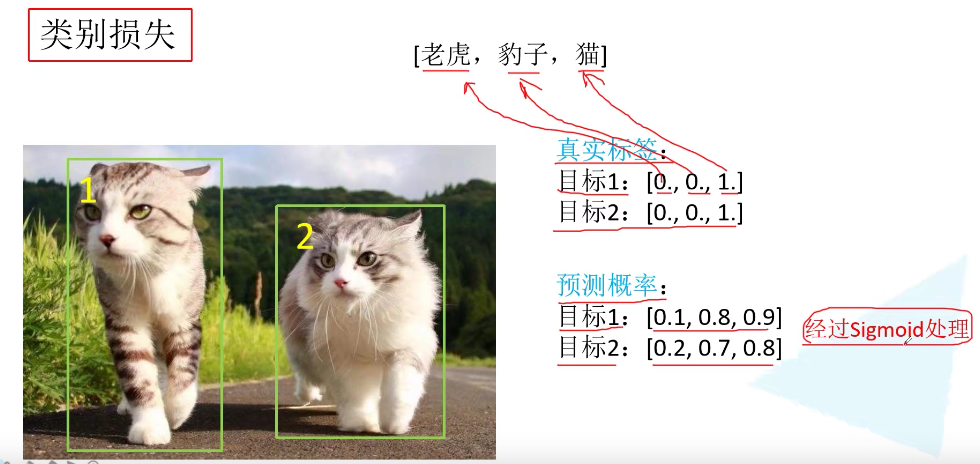
类别损失也是使用二值交叉熵损失，这个与原文表述一致。

img10

需要注意的是，COCO 数据集有 80 个类别，所以类别数在 85 维输出中占了 80 维，每一维独立代表一个类别的置信度。作者使用 Sigmoid 激活函数替代了 YOLOv2 中的 softmax，取消了类别之间的互斥，可以使网络更加灵活。但是经过 Sigmoid 处理可能出现认为目标既是猫又是狗的情况（两个概率都大于 0.5）。所以 80 个概率之和并不是等于 1 的。

img11

上述公式是否正确呢？通过实践其实可以检验，关于 PyTorch 官方对于 BCELoss 的描述可以参见 此处：

import torch
import numpy as np

loss = torch.nn.BCELoss(reduction="none")		# reduction="none" 不进行求均值处理
po = [[0.1, 0.8, 0.9], [0.2, 0.7, 0.8]]
p = torch.tensor(po)
p.requires_grad_()

go  = [[0., 0., 1.], [0., 0., 1.]]
g = torch.tensor(go)

l = loss(input = p, target = g)
print(np.round(l.detach().numpy(), 5))			# detach() 去除梯度信息

print("------------------------------")

def bce(c, o):
    return np.round(-(o * np.log(c) + (1 - o) * np.log(1 - c)), 5)

pn = np.array(po)
gn = np.array(go)

print(bce(pn, gn))

'''
[[0.10536 1.60944 0.10536] 
 [0.22314 1.20397 0.22314]]
------------------------------
[[0.10536 1.60944 0.10536] 
 [0.22314 1.20397 0.22314]]
'''
1.4.3 定位损失

论文中写道，在训练过程中使用平方差损失。也可以使用出自 Faster R-CNN 的 smooth L1 loss，smooth L1可以使训练更加平滑。在 YOLOv3+SPP 中定位损失会使用 GIOU。

img12