深度学习之目标检测(四)SSD算法理论
本章学习 SSD 相关知识,学习视频源于 Bilibili。
Faster R-CNN 存在的问题:
- 对于小目标检测效果很差
- 个人看法:只在一个特征层上进行预测 (FPN对此进行了改善),而这个特征层经过很多卷积层,已经被抽象到高层语意了,抽象层次越高,细节信息的保留越少。而检测小目标需要细节信息。
- 模型大,两阶段,检测速度较慢
- 主要原因还是因为两阶段,在 RPN 和 fast R-CNN 处进行了两次预测。这是两阶段网络的通病。
既然高层次的 feature map 保存的细节信息比较少,那么能不能在相对低一点的层次上进行预测呢?
既然两阶段目标检测器效率低,能不能直接摈弃了proposal的生成阶段,生成全部 anchor box 来做单阶段呢?
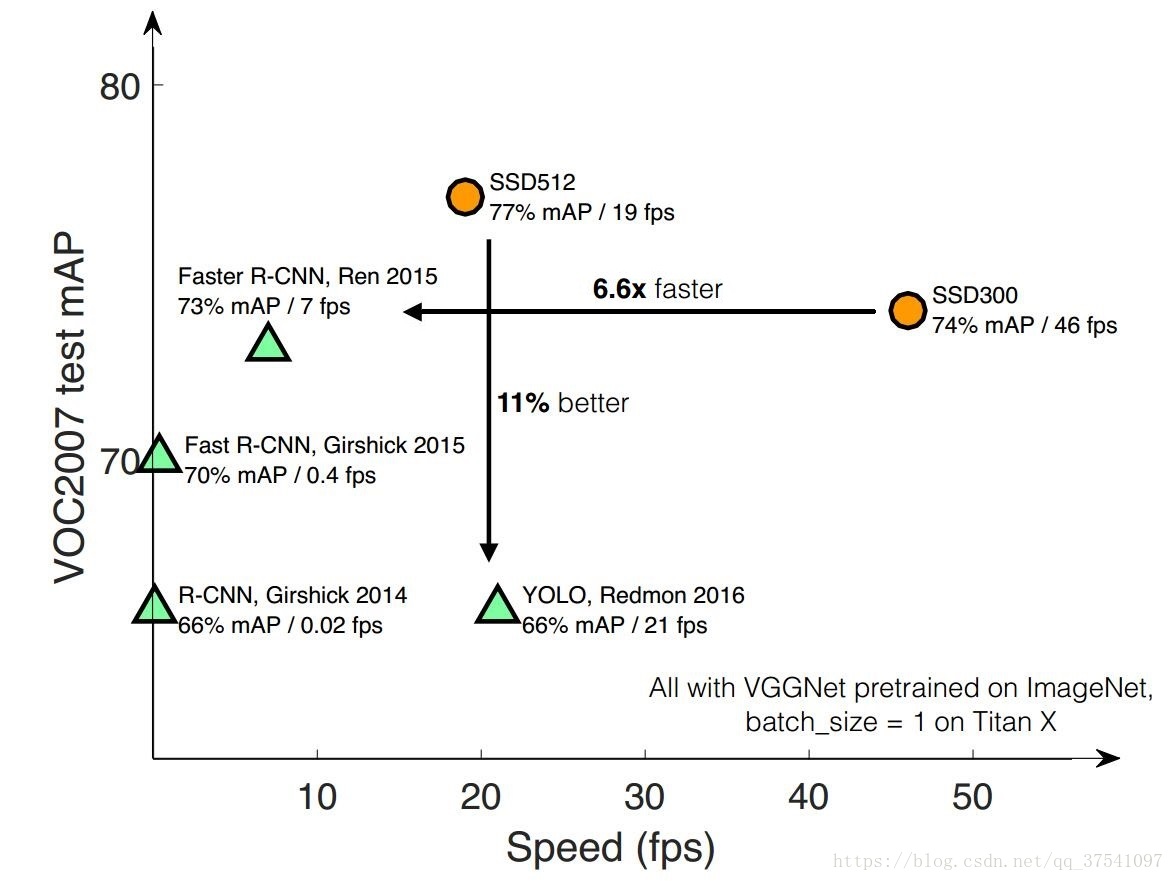
1. SSD – 真正的实时,单阶段检测器
SSD 原始论文为发表于 2016 ECCV 的 SSD: Single Shot MultiBox Detector。对于输入尺寸为 $300 \times 300$ 的网络使用 Nvidia Titan X 在 VOC 2007 测试集上达到了 74.3% mAP 以及 59 FPS (每秒检测59张图片)。对于输入尺寸为 $512 \times 512$ 的网络达到了 76.9% mAP,超越了当时最强的 Faster R-CNN (73.2% mAP)。
SSD 结构如下图所示:

1.1 预测特征层
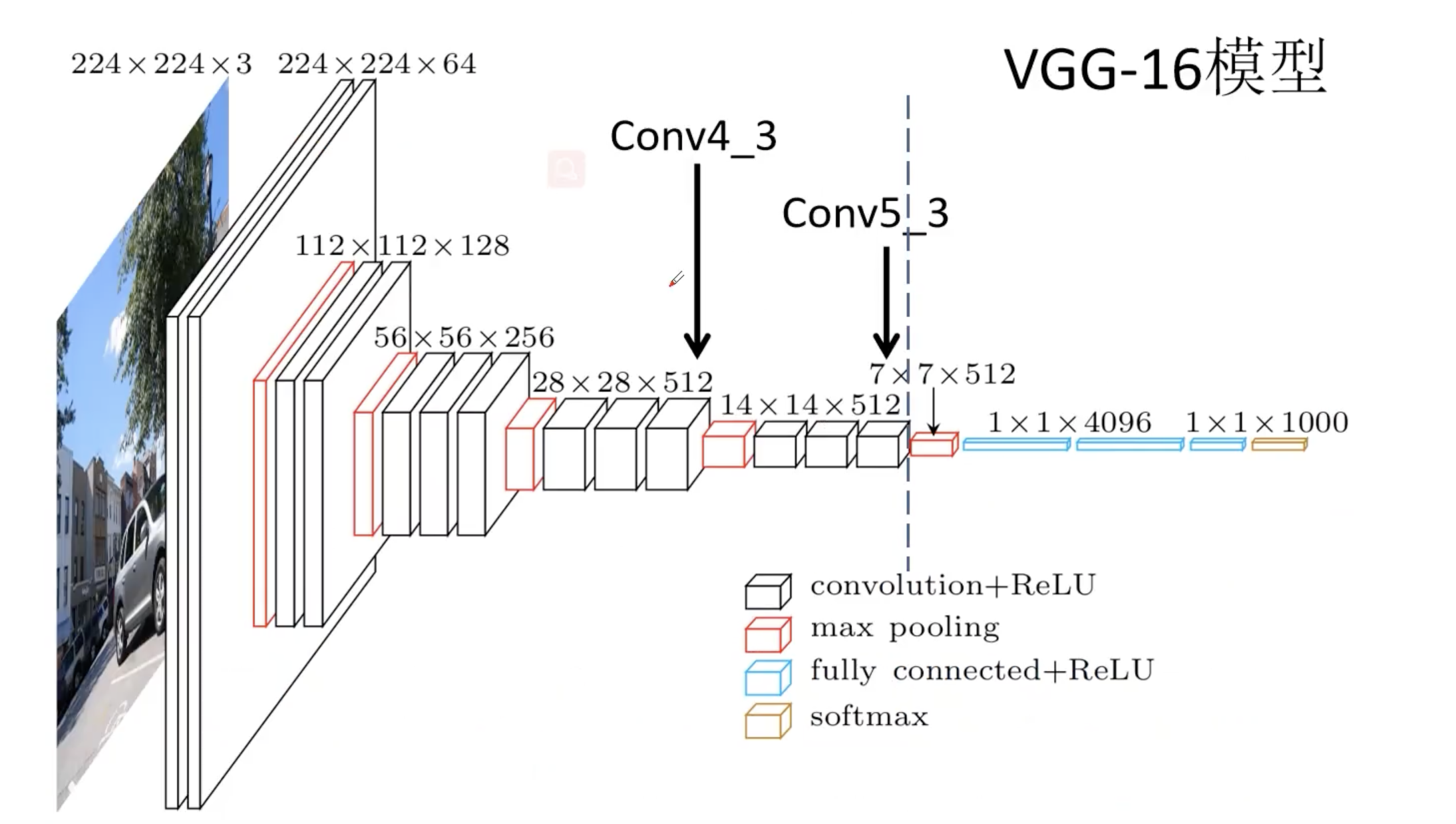
输入图像为 $300 \times 300$ 的,因为后面有展平连接,特征图大小必须固定。图像首先被 resize 到 $300 \times 300$ 的尺寸,然后输入 VGG-16 的 backbone。其中 Conv4_3 得到的是 SSD 的第一个预测特征层。注意到 max pooling 5 从 $2 \times 2$,stride 为 2 变为 $3 \times 3$,stride 为 1。所以通过新的 pooling 层之后特征图的宽和高是不会变化的,还是和原来一样的。经过新的 pooling 层之后输出的是 $19 \times 19 \times 512$ 的特征图。在其后面再添加一系列卷积层,获得其他的预测特征层,注意到 $3 \times 3$ 卷积层的步距是不一样的,有 2 也有 1,有些 padding 也不一样。一共有 6 个预测特征层。
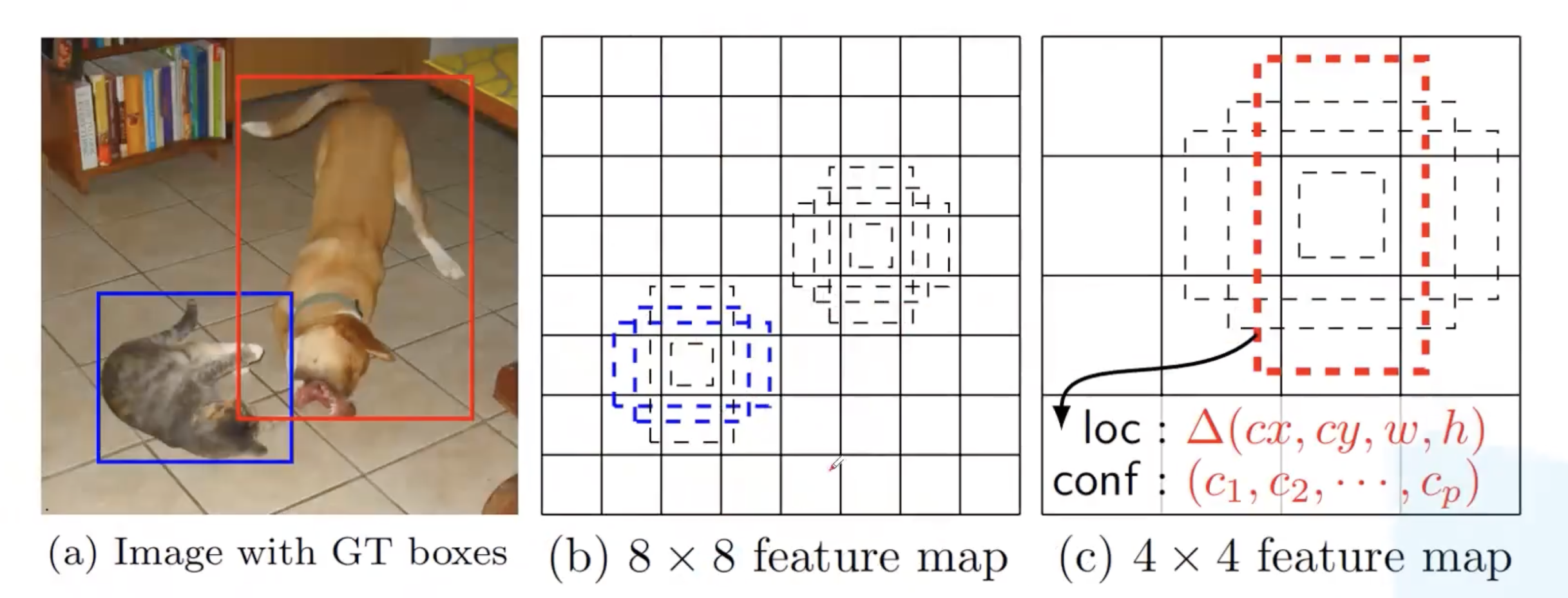
为了方便理解,我们分析一下原论文给出的示例。最左边为标注好的原图,然后有两个特征矩阵,分别为 $8 \times 8$ 和 $4 \times 4$。 $8 \times 8$ 的特征矩阵相较于 $4 \times 4$ 的特征矩阵抽象程度更低一些,细节信息保留更多一些。所以我们在相对底层的特征图上预测较小的目标。比如猫的面积相比于狗就会小一些,所以在 $8 \times 8$ 的特征图上预测猫的目标边界框,在 $4 \times 4$ 的特征图上预测狗的目标边界框。从而提升小目标的检测效果。
1.2 Default Box
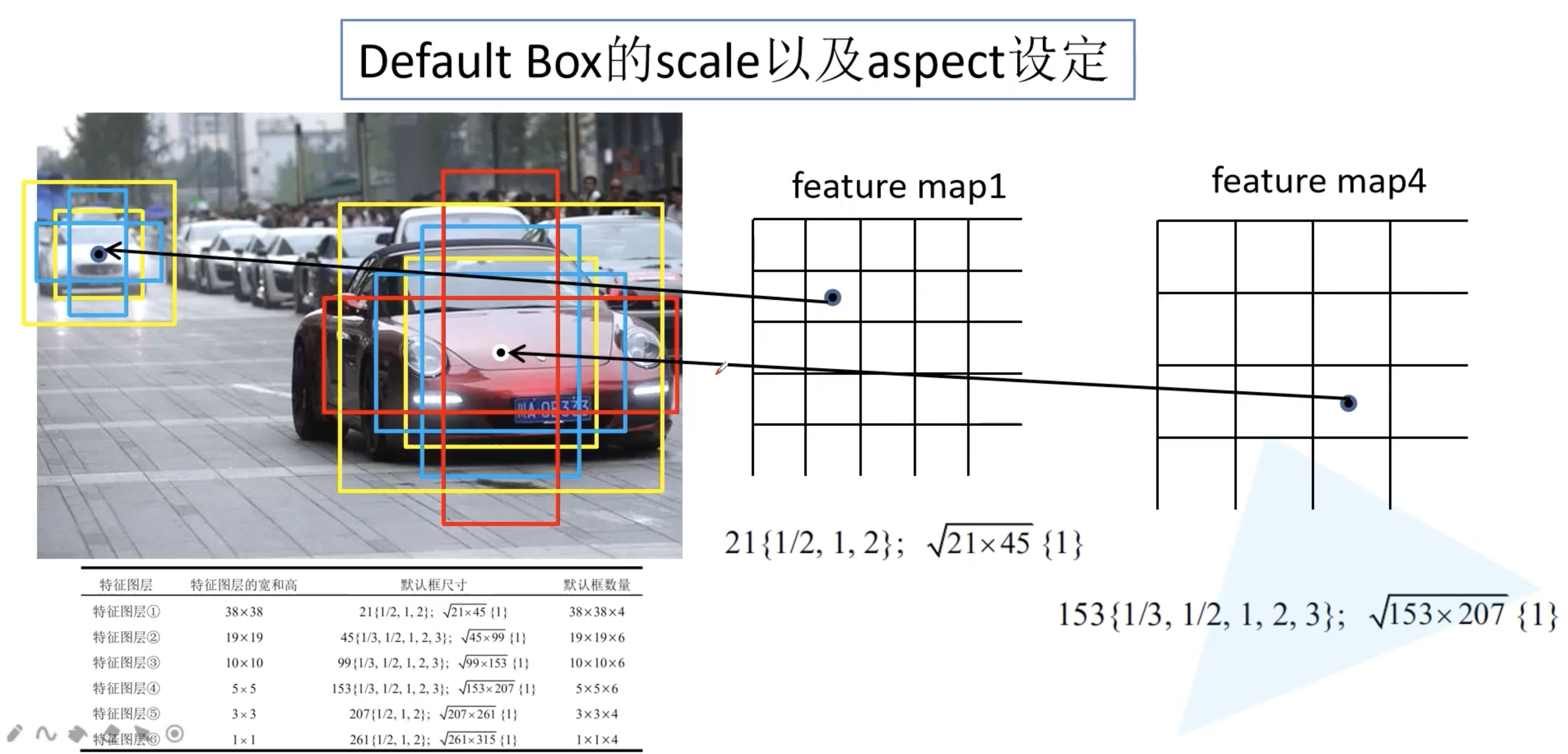
SSD 中使用的 Default Box 其实和 Faster R-CNN 中的 anchor box 相近。我们来看看 Default Box 尺度和比例的设定。下图来自于原论文。其实原论文的 Scale 计算公式 4 会发现和 github 上很多开源的实现并不一样。

所以我们直接来看看 scale 和 aspect 的参数。为什么每个 scale 有两个值?在原论文中写到 (上面那张图中的下划线),如果 aspect 比例为 1,在每一个特征层上面会额外添加一个 default box 的 scale, $S_k’ = \sqrt{S_k S_{k+1}}$。$S_k$ 对应的就是 scale 中的第一个元素,当前层的 $S_{k+1}$ 对应的就是下一层的 $S_k$。此外,对于 conv4_3,conv10_2,conv11_2 的特征层使用 4 个 default box,其他特征层都使用 6 个 default box。言外之意则是:图片中大的物体和小的物体占少数,比例更固定,中等物体占多数,比例更多样。(1, 2, .5) 分别表示 1:1, 2:1 以及 1:2。对于 $\sqrt{21 \times 45}$ 的 scale 只有 1:1 这个比例。

| 下表给出了每一个预测特征层的高和宽,以及在该层所预测的 default box 的信息。在 6 个特征图上会生成 38 x 38 x 4、19 x 19 x 6、10 x 10 x 6、5 x 5 x 6、3 x 3 x 4、1 x 1 x 4,也就是 5773、2166、600、150、36、4,加起来一共有 8732 个 default box (同样是滑动窗口)。 其中 default box 的中心点坐标为: $((i + 0.5) / | f_k | , (j + 0.5) / | f_k | )$ , $f_k$ 为第 k 层的feature map 的大小。 |

为了更进一步方便理解 default box,下图例举了两个预测特征层。首先找到对应坐标,然后确定 box。这其实看起来和 Anchor box 差不多。将所有特征图上的所有 default box 绘制到原图基本就能覆盖原图出现的所有物体了。
1.3 Predictor
了解完了 default box,我们来看看预测器 predictor 的实现。如何在六个预测特征矩阵上进行预测?原论文中写道:对于尺寸为 $m \times n$,通道数为 $p$ 的特征层,直接使用卷积核大小为 $3 \times 3 \times p$ 的卷积核进行实现,生成预测概率分数和相对 default box 的坐标偏移量。对于特征图上的每一个位置的 k 个default box,每个 default box 生成 c 个类别分数和 4 个坐标偏移量(x, y, w, h),并不关心每个坐标回归参数属于哪个类别(这与 Faster R-CNN 不同),需要 (c+4)k 个卷积核。所以对于 $m \times n$ 的特征图而言,就会生成 (c+4)kmn 个预测输出值。


(c+4)k 个卷积核,其中 ck 个用于预测目标类别分数,4k 对应的是每个 default box 的边界框回归参数。注意到:这里的 c 是包括了背景类别的。例如对于 PASCAL VOC 数据集,c 就是 21。在 feature map 的每个位置都会生成 k 个 default box。
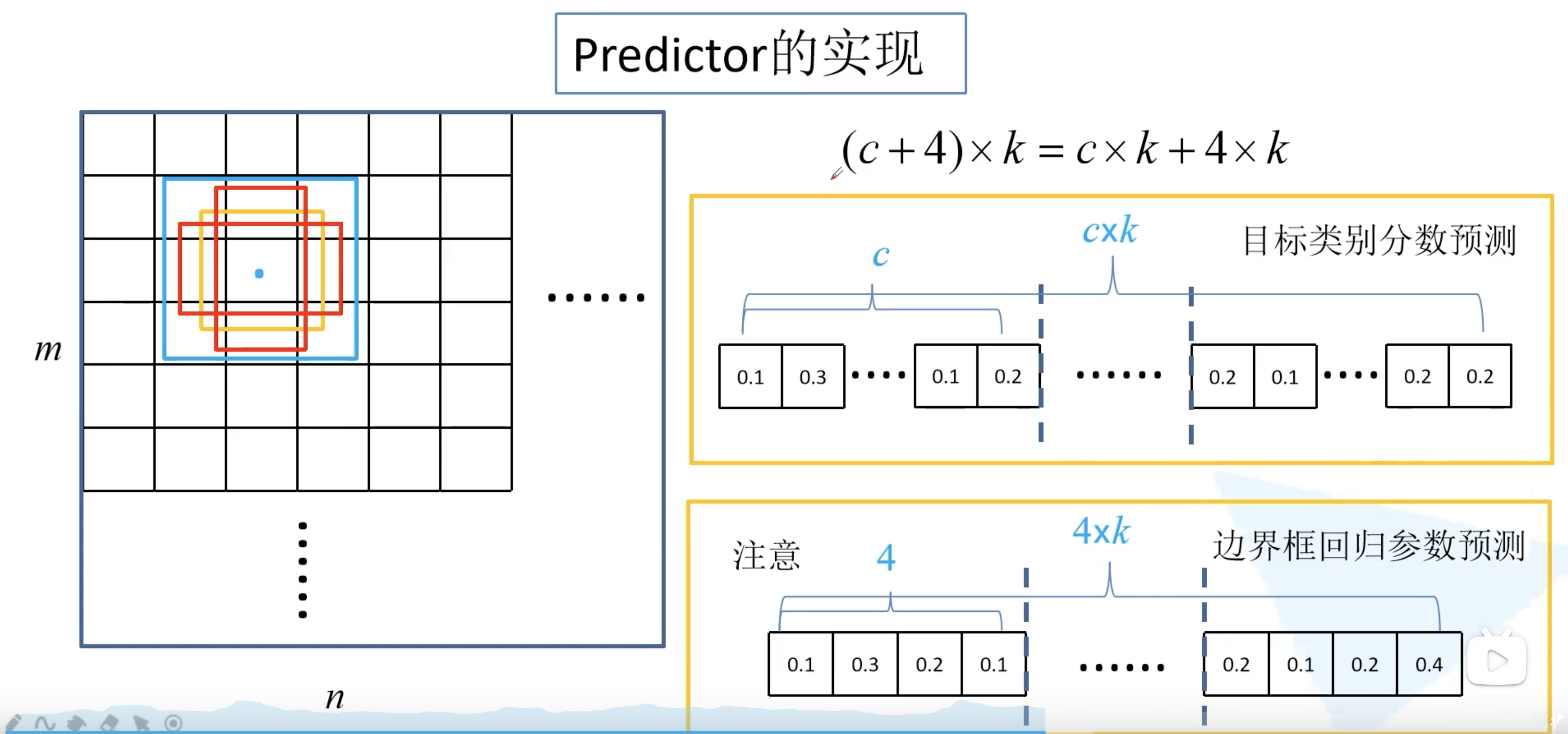
基于类别预测分数,将这 8732 个 default box 送入 NMS 非极大值抑制模块中,获得最终的检测结果。
1.4 训练过程中正负样本选择
对于正样本的选取,论文中给出了两个准则,首先是与 ground truth 匹配 iou 最大的 default box;第二个匹配准则则是与任何 ground truth 的 iou 值大于 0.5。这与 Faster R-CNN 也比较类似。其实虽然生成了 8 千多个 default box,真正属于正样本的其实很少,基本就是几个到十几个。剩下的全当负样本肯定不好,带来样本不平衡问题。对于剩下的样本,首先计算 confidence loss,意味着网络将这个负样本预测为目标的概率越大,这是不能容忍的。所以选择 confidence loss 靠前的负样本,且负样本和正样本比例为 3:1。该方法在论文中被称为 Hard negative mining。


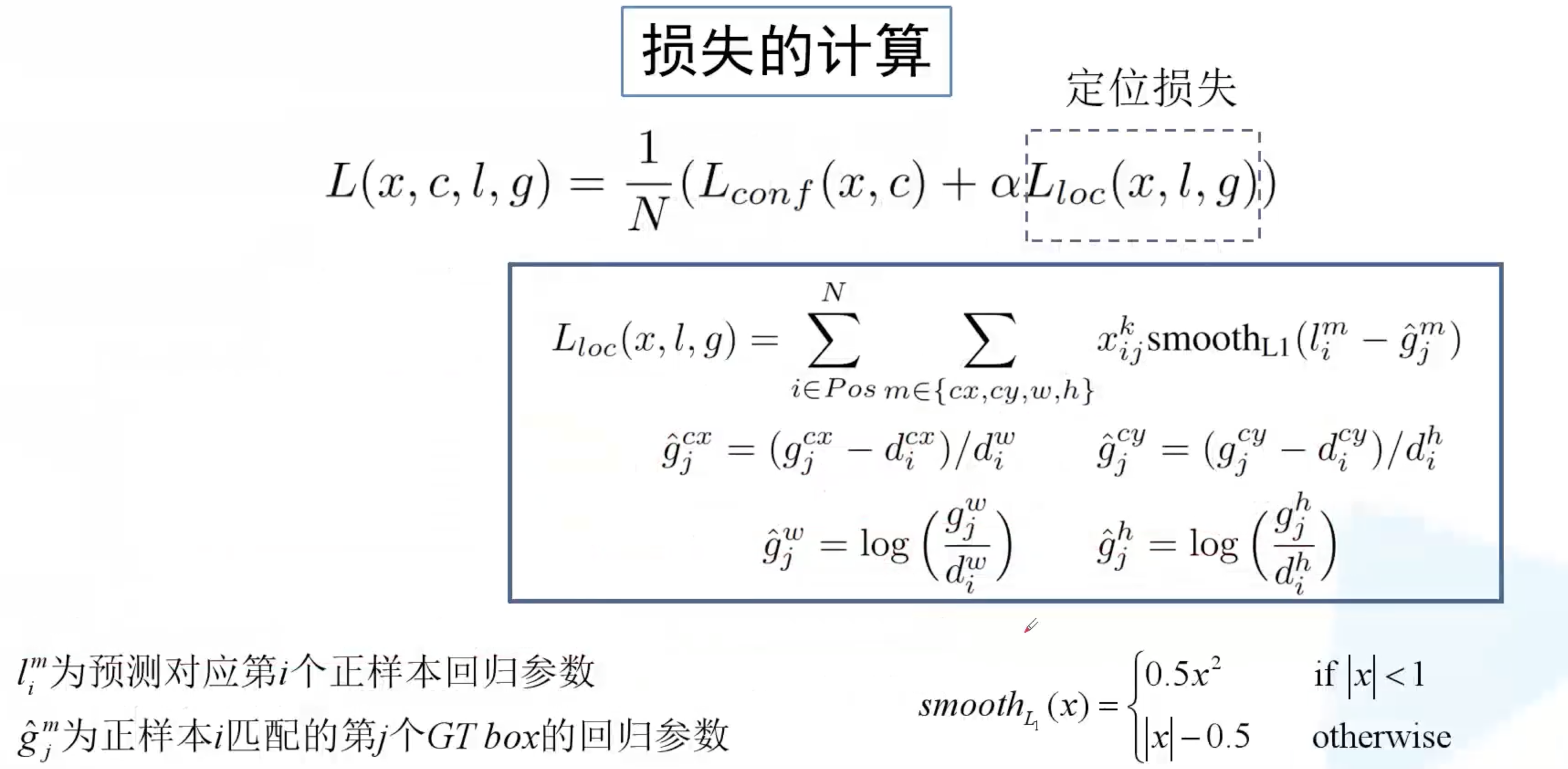
1.5 损失计算
损失依然分为两部分,类别损失和定位损失,N 为正样本个数,$\alpha$ 为平衡系数。

类别损失分为两部分,第一部分为正样本的类别损失,第二部分为负样本的类别损失。第一项是让 default box 的 GT box 类别预测概率值接近于 1;第二项是说网络预测负样本的类别为 0 的概率分数接近于 1,即负样本的类别为 0。

定位损失则仅针对正样本而言,定位损失以及回归参数的计算方式都与 Faster R-CNN 是一样。
1.6 总结
SSD算法也同样产生了很多后续工作比如 DSSD、RefineDet等等,知乎 有简单的专栏综述,后续将继续进行学习。
DSSD: Deconvolutional Single Shot Detector
FSSD:Feature Fusion Single Shot Multibox Detector
RefineDet: Single-Shot Refinement Neural Network for Object Detection
RfbNet:Receptive Field Block Net for Accurate and Fast Object Detection
M2Det: A Single-Shot Object Detector based on Multi-Level Feature Pyramid Network
Pelee:Pelee: A Real-Time Object Detection System on Mobile Devices
