稀疏表示学习(五)
本次主要学习资料是Duke大学Guillermo Sapiro教授的公开课——Image and video processing, by Pro.Guillermo Sapiro 课程。该课程可以在 Bilibili 上找到学习资源。
1. 结构化稀疏模型与高斯混合模型 Structured Sparse Models and Gaussian Mixture Models
Structured Sparsity 是在标准稀疏算法基础上,修改惩罚项而成。约束项为图像先验信息,迫使学习特征按照一定规则排列,行成有结构的字典。
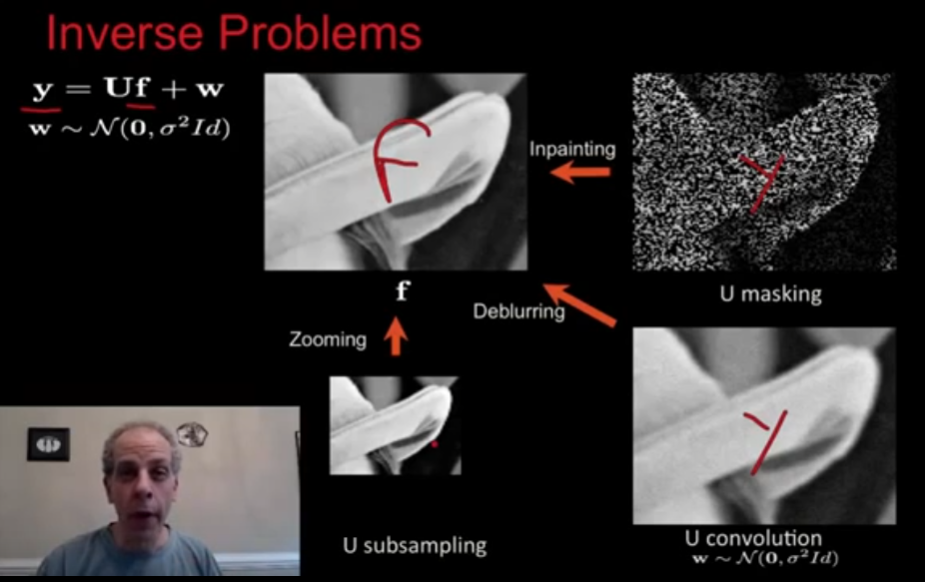
我们要从 $y$ 恢复出来 $f$。我们考虑 $f$ 是干净无噪的图片,我们观测到的是 $y$,他其实是 $f$ 经过了某个变换 $U$,再加上高斯噪声 $w$。$U$ 可以是 Mask 矩阵,可以是缩放操作,也可以是(模糊)卷积。
Gaussian Mixture Models of Patches
我们的想法是,为图片 $f$ 的每个 patch $f_i$ 进行建模,由于可能每个 patch 的变换不同,所以使用对应的 $U_i$。噪声依然是高斯噪声。现在我们将对此进行建模。
信号具有 $K$ 个不同的高斯子信号,因此基本上我们可以知道如果色块是 $8 \times 8$ 大小的,我们将和以前一样有一个对应的 64 维度的向量。为此我们要使用 $K$ 个 64 维的高斯模型进行建模。我们需要计算这 64 维向量的平均值和协方差。
高斯等效于将模型作为主成分分析的PCA,基本思想是,我们可以计算此协方差矩阵的特征值和特征向量,特征向量可以给我们一个字典,其中有 64 个 atom。假设 $K = 10$,那么我们就得到了 640 个 atom 的字典。
现在每一个 patch 都由其中一个进行建模。我们要做的就是从带噪图像中估计图像的知识或者模糊因子等。然后确认哪个高斯是适合这个 patch 的,并且从这个高斯模型中估计出来这个 patch。
(上述部分其实听课听的二懂二懂的,希望有人能够进行补充)

Structured and Collaborative Sparsity
普通的稀疏建模中我们有一个很大的过完备的字典,我们可以选择所有的 atom,我们可以从一个很大的 $K$ 中选择不超过 $L$ 个 atom 来进行信号的稀疏表示。我们的选择可能有 $C(K, L)$ 种,这是非常大的数。我们有大量的子空间可供选择。这样的生成模型非常丰富,这是他的优势。但是另一方面,这样的模型非常不稳定,我们有太多的可以选择,我们在图像或者 patch 进行微小的更改,最终选择可能非常不同。
如果考虑高斯混合模型,这与进行主成分分析等价,因此我们采用协方差矩阵,分解它以获得本征向量。我们一共有 K 个高斯模型,将协方差矩阵连接起来,所以这是一个个高斯的协方差矩阵。
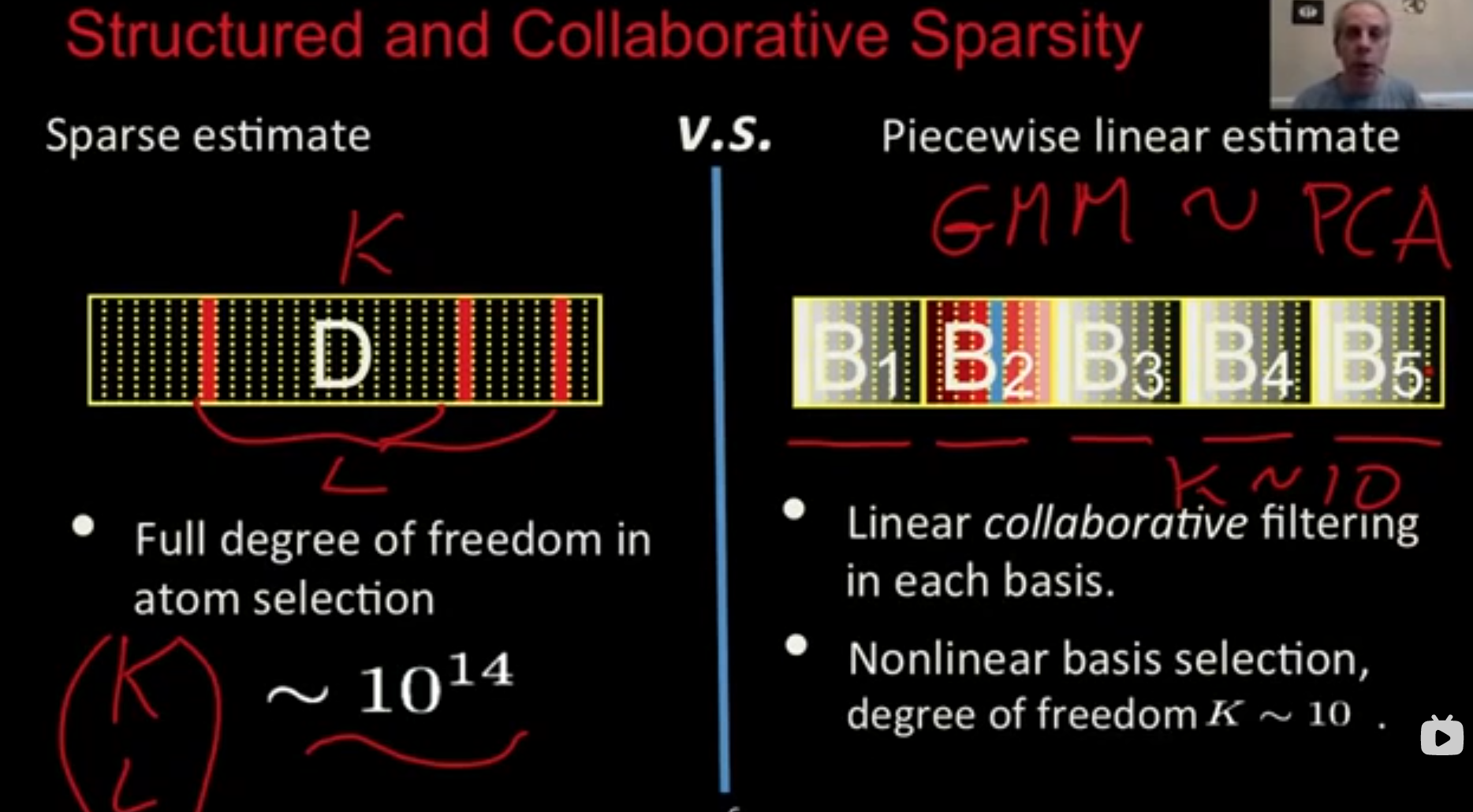
当我们选择了一个高斯,其实是选择了这个高斯块,然后我们最好地拟合高斯。这大概只有10到20个选项(由K决定)。一旦选择了高斯,就只需要将其投影到其中就行了。
在左边,每个atom都是独立的;然而在右边,我们学习的字典有块状结构,并且在投影时选用整个块,这就是结构稀疏性的概念。基本上原子是有相关性的,要么它们聚在一起,要么他们根本没有被选择。这就是块非常特殊的地方,结构之间没有重叠,我们只能选择一个。这会使得系统更稳定。 事实证明,只要有20个高斯,基本就可以得到与一些普通字典一样的效果。但是算法简单很多,也稳定很多。
