稀疏表示学习(三)
本次主要学习资料是Duke大学Guillermo Sapiro教授的公开课——Image and video processing, by Pro.Guillermo Sapiro 课程。该课程可以在 Bilibili 上找到学习资源。
1. 字典学习 - Dictionary Learning
我们已经讨论了关于 $\alpha$ 的稀疏表示,那么字典应该是什么?
我们的基本假设是:Good-behaved Images have a sparse representation.
为此,应该是鼓励稀疏性的字典。D should be chosen such that it sparsifies the representations.
- 一种方式是选择已有的变换集:小波包,傅立叶变换,离散余弦变换等等。
- 另一种方式则是从大量的数据中学习字典。

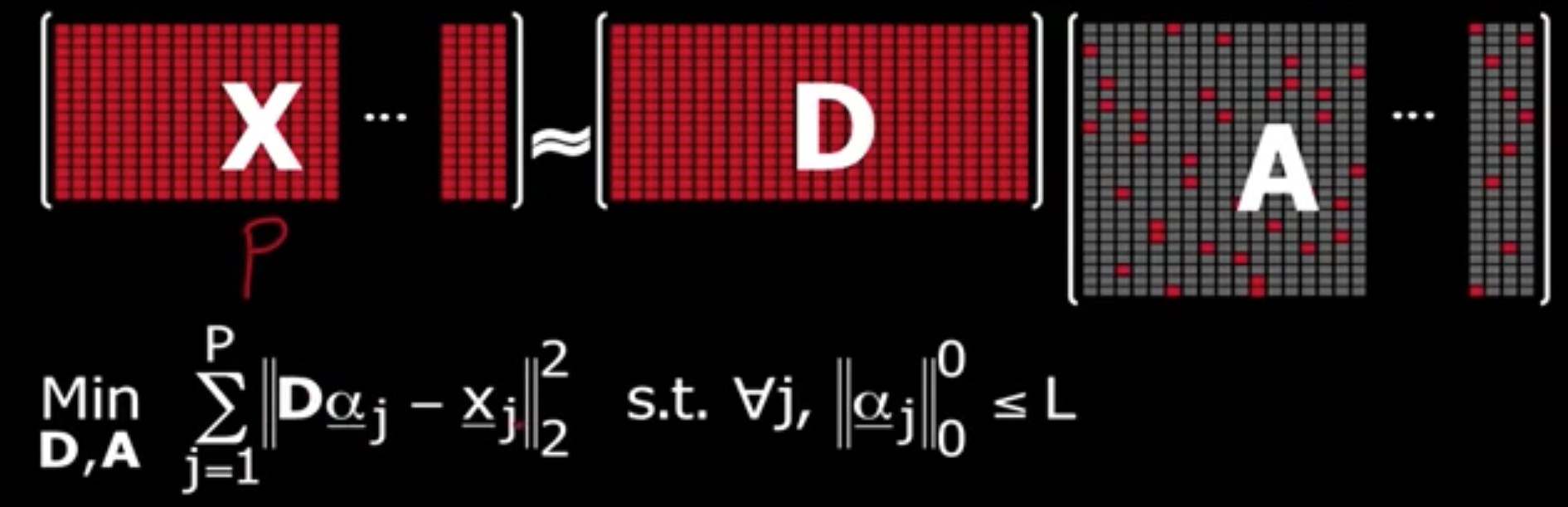
我们有 P 个数据样本,希望学习到一个字典,它能够使得每个样本都能有稀疏表示。经典的算法是:K-SVD。
我们有所有的信号,将其写为 $X$。
- Step1: 我们要学习字典 D,我们可以通过任何方式对其进行初始化,例如从 P 个信号中随机选择 K 个信号来作为初始化的字典也是可以的。
- Step 2: 我们将使用字典进行稀疏编码,这部分在上一节已经讲到了。每一行就是每个信号的稀疏表示,红色表示非零系数。
- Step 3: 则是更新字典,基本思想是我们朝着另一个方向进行稀疏编码。
- 之后再回到Step 2,直到收敛。
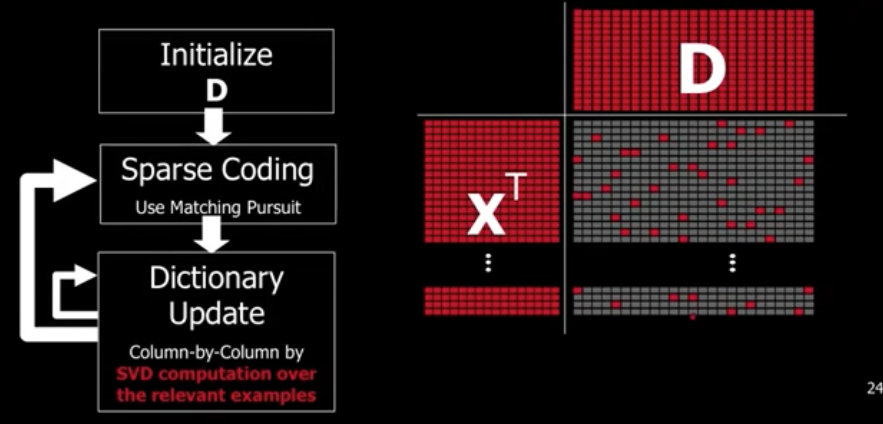
Step 2: Sparse Coding Stage
对每一列使用之前学到的稀疏编码表示计算,例如放缩或者贪心算法。我们没有直接对 $j = 1$ 到 P 进行求和,而是一行一行的对每个信号进行计算。最终我们得到了整体的稀疏表示矩阵 A。

Step 3: Dictionary Update Stage
我们一次要更新一个 atom。我们如何进行更新呢,以第k个 atom 为例。我们首先选出所有稀疏表示使用了这个 atom 的信号,现在要使得 atom 对于这些信号更好。
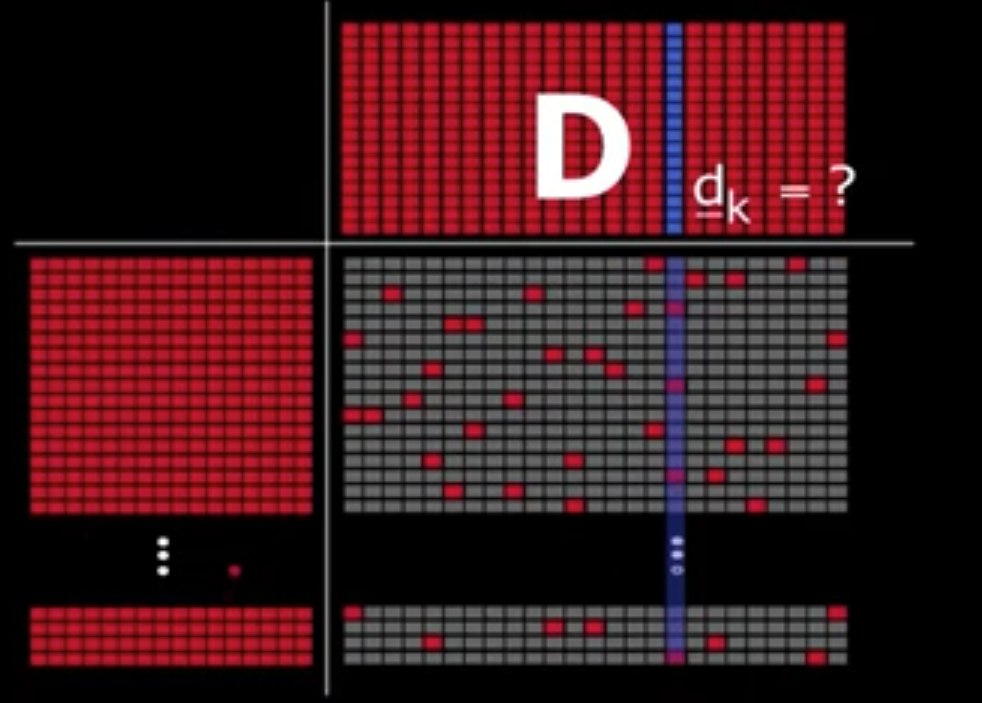

固定 A 和 D 除了第k列外的其他值不动,原信号减去除了选中的第k个atom外其他atom的贡献。绿色部分就是信号剩下的部分。我们将重新设计 atom 来最小化这个误差。这里的 E 就是绿色的部分。我们可以直接通过 SVD 分解来解决这个问题。
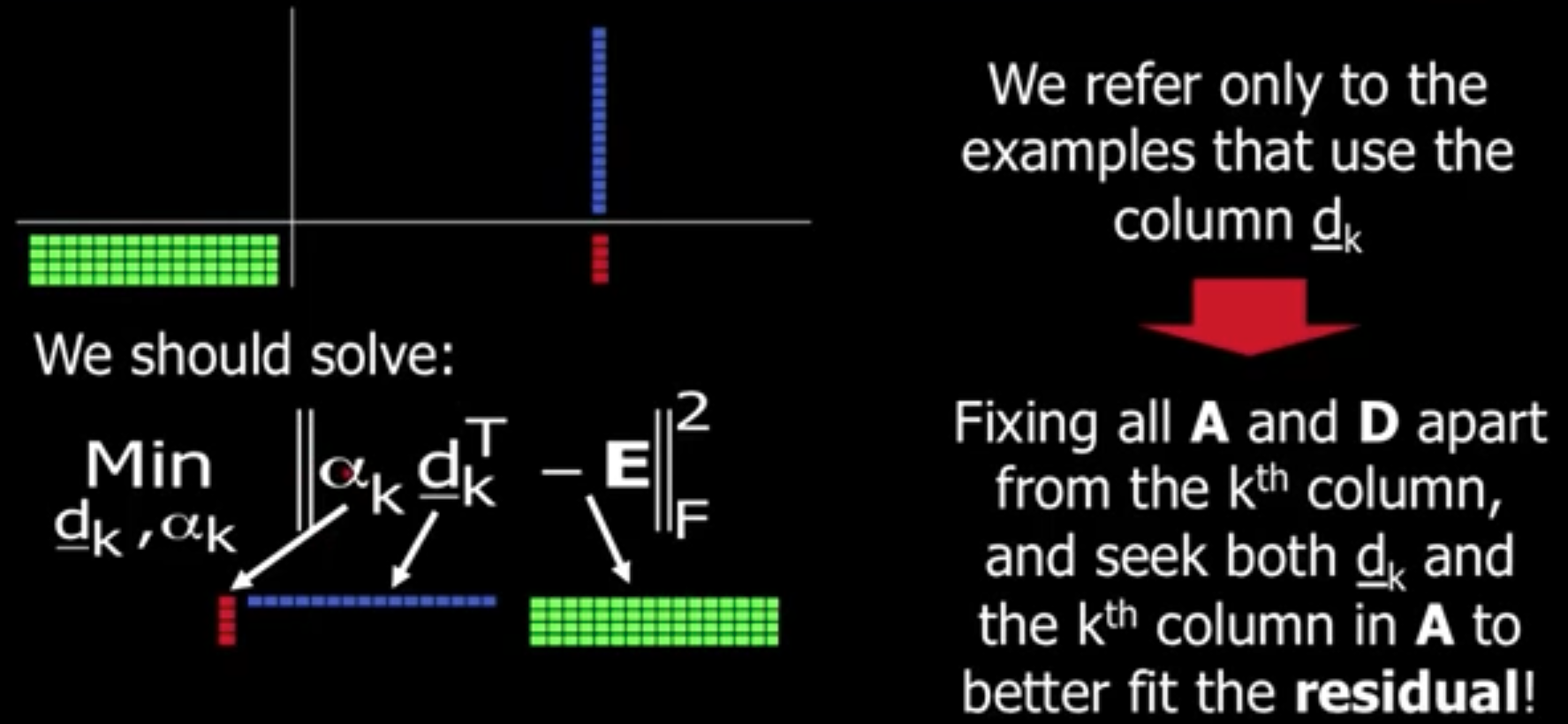
这样修改之后,对于其他信号而言,以及对于选中的信号的其他稀疏表示系数而言都不会有更改。只是更改了第k个 atom 以及信号对应的稀疏表示系数。
2. 总结
我们经常通过随机采样一些信号来初始化字典 D,为什么不选择一些其他信号都是这些信号的稀疏表示的,来初始化呢?这些都归属于字典学习范畴研究的问题。
