稀疏表示学习(一)
本次主要学习资料是Duke大学Guillermo Sapiro教授的公开课——Image and video processing, by Pro.Guillermo Sapiro 课程。该课程可以在 Bilibili 上找到学习资源。
本节部分笔记参考 https://www.cnblogs.com/daniel-D/p/3222576.html。
1. 稀疏建模介绍 - Sparse Modeling
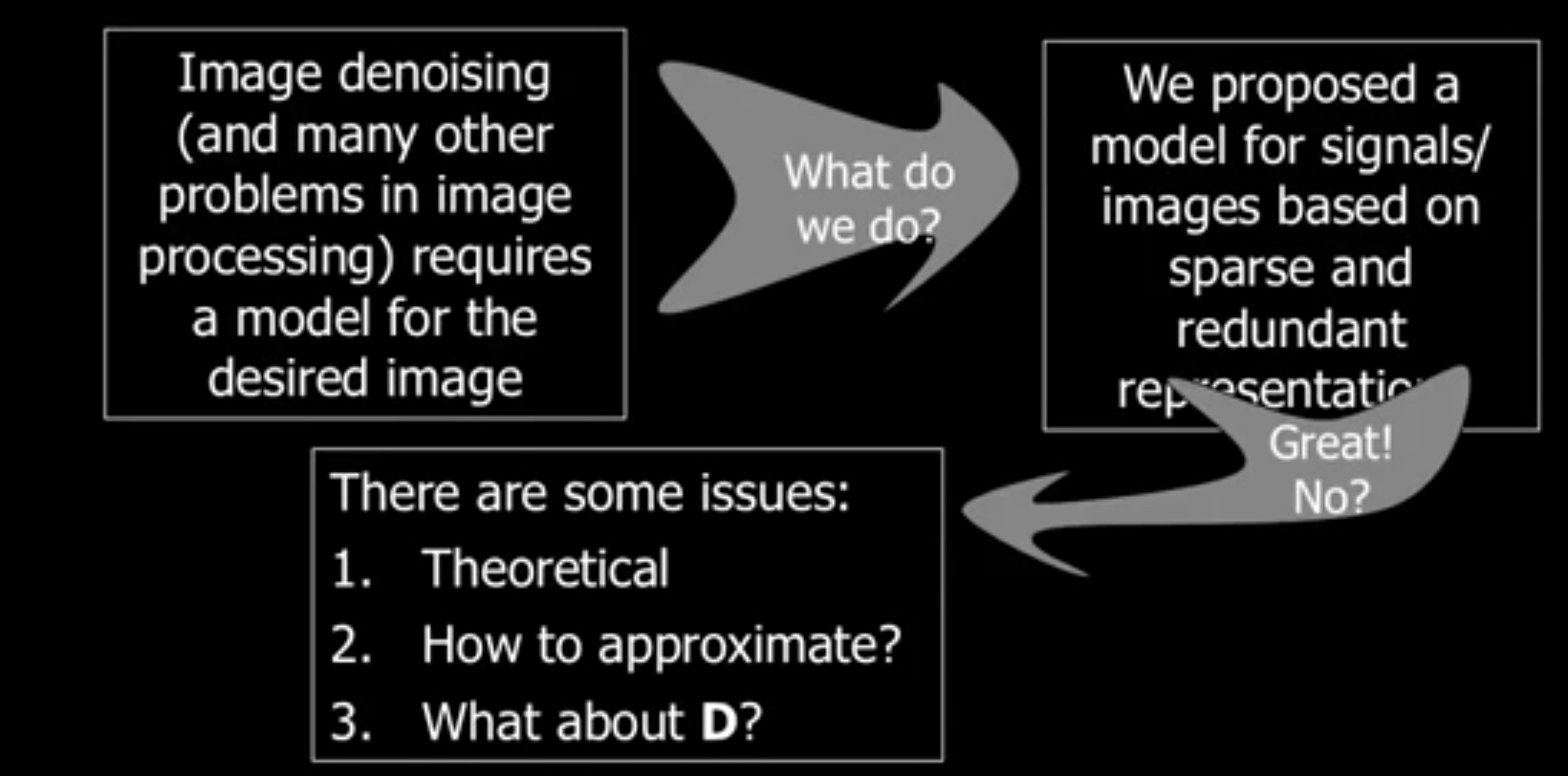
图像去噪是一个很好的例子来引入稀疏建模。手上有噪声的图像如何变成干净的图片呢?

该问题可以建模为如下形式:$y$ 是含有噪声的图像,$x$ 是未知的无噪图像。下式第一项表示不想让恢复图像距离含噪图像太远,这里用图像之间的均方误差作为惩罚。如果加的是高斯噪声,那么这里就是方差。如果只有第一项,那么最优解无非就是带噪图像本身。后一项 $G(x)$ 被称为先验,也叫正则化项。也就是无噪图像 $x$ 具有某些属性、
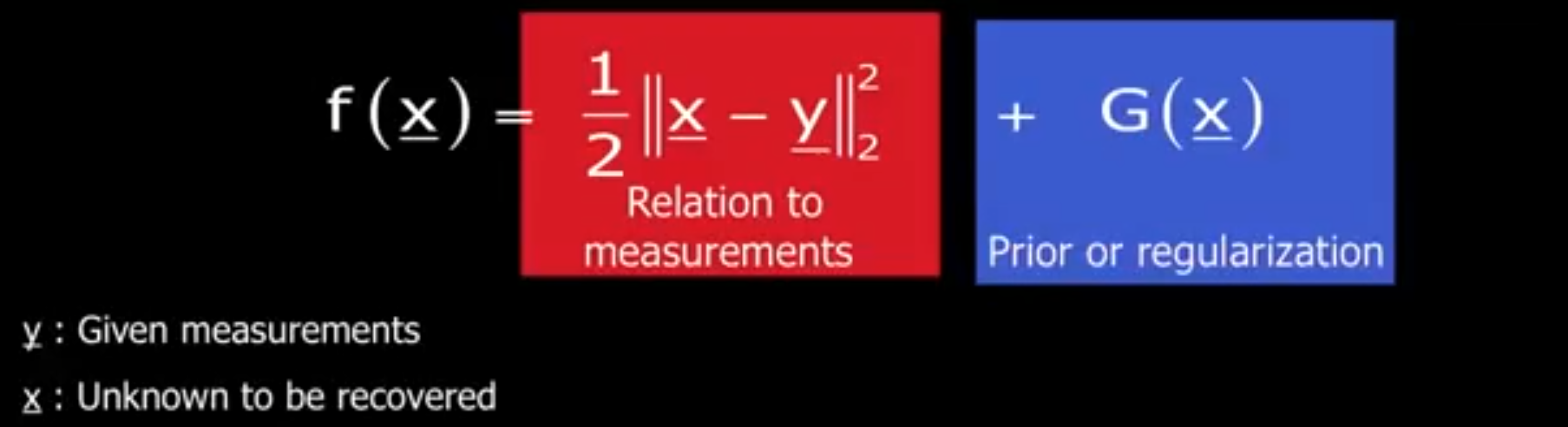
第一项称为likelihood,第二项是prior,都可以进行概率解释。假设 $x$ 本来是就带有某种先验概率的分布,现在又已知观测值 $y$, 根据贝叶斯原理, 现在 $x$ 的分布(后验)正比于先验概率分布与高斯分布的乘积。如果先验概率分布也正是指数分布,将乘积取负对数,就可以得到上述在机器学习里非常常见的 MAP 模型。
现在的问题是:最好的先验 (prior) 究竟是什么? G(x) 应该取什么形式? 定义图像信号的最好空间是什么?

第一张图, prior 假设 clean image 能量尽量小, x 要尽可能地小。第二张图, prior 认为恢复后的图像要光滑,于是产生了 Laplacian 和 low energy 的结合,朝前进化了一步。第三张图,prior 认为要考虑 edges 是不光滑的,需要不同情况不同处理…… Sparse and Redundant 是正在讨论的问题,目前是最新的进化版本,而后面也有一些算法,虽然也成功进化成人类,可惜太胖了,行动不便—— computationally expensive and difficult。 Sparse modeling 的先验究竟是什么?要回答这个问题,还需要了解一些基础概念。
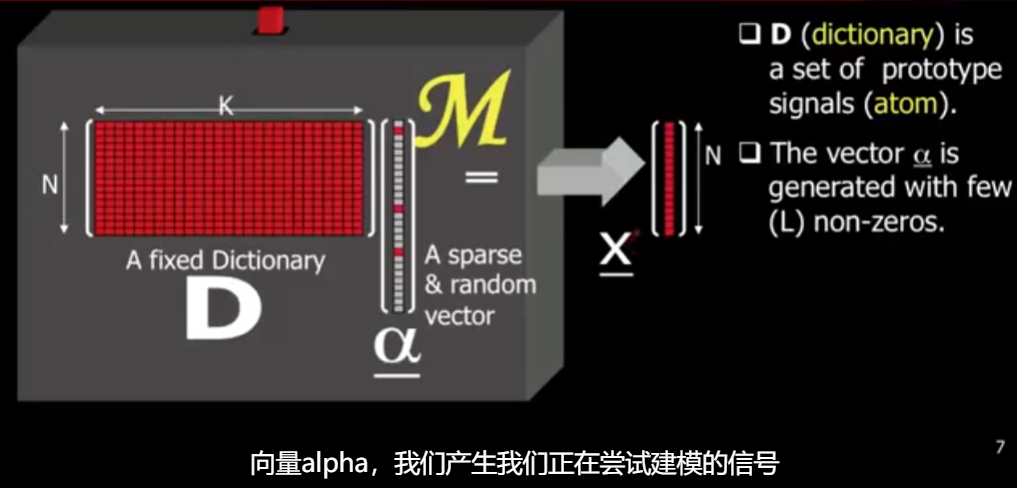
定义:Dictionary is a set of prototype signals (atom).
字典是一个矩阵,它是 $n\times k$ 的,其中 $n$ 是信号的维度,$k$ 是字典的大小。字典有 $k$ 列,每一列称为一个原子,它可以是一种图像,一个 patch。通常 $k>n$。如果 $k>n$,我们称其为过完备的(over complete)。如果 $k=n$,我们称其为完备的(complete),例如傅里叶或者离散余弦变换等。如果 $k<n$,我们称其为非完备的(under complete)。
向量 $\alpha$ 最多有 $L$ 个非零元素。$D \alpha$ 其实就是非零原子的线性组合。向量 $\alpha$ 非常稀疏。这也是稀疏表示的来源。
如果字典大小为 $k$,我们选择 $L = 3$,那么一共有 $C(K, L)$ 中选择,每一种选择都会定义一个非常低维的子空间,我们有许多的子空间。
例如 JPEG 图像,$D$ 是 $\cos$ 余弦基,$\alpha$ 是余弦变换的系数。当我们量化大量离散余弦变幻时,我们看到它们大量系数变为 0。所以仅仅需要几个系数就可以很好地表示一个 $8\times 8$ 的部分。
下一个问题是:如何测量稀疏度?
衡量稀疏性的方法是 LP-norm。
-
如果 $p = 2$,我们就不能真正得到我们想要的东西,因为我们想要的是每当 $\alpha$ 的输入项之一不为 0 时,有等额的惩罚。
- 当 $p = 1$ 时,至少现在的惩罚是成正比的。与系数的大小成线性比例,而不是二次方。
- 如果 $p < 1$,如果系数为 0,那么我们真正想要的惩罚为 0,然后只要系数不为 0,惩罚就趋于平缓。
- 如果 $p -> 0$,我们得到的正是我们想要的对所有非零系数有相同的惩罚。
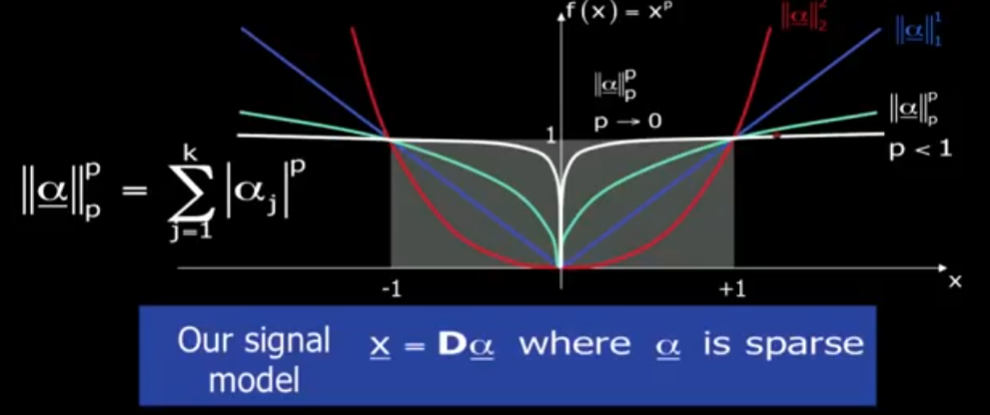
实际上我们希望不管 x 多大,它非零的惩罚是相同的, $L_0-\text{norm}$正好满足这个要求,它表示的意思是数出 alpha 向量中非零的个数。所以我们测量稀疏度的方法是 $L_0-\text{norm}$。

补充理解
假设字典 $A$ 矩阵 $K > N$,并且是满秩的 (图中是 $D$ ),那么对于任意一个 $N$ 维的向量 $b$ (图中是 $x$ ),肯定有 $Ax = b$。现在加入 Lp-norm 的约束条件,限制只能用少量的 $A$ 的列向量 (atoms 作为基,向量 $b$ 就被固定在某个 span 内,成为了一个 Lp 优化问题:
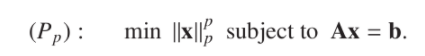
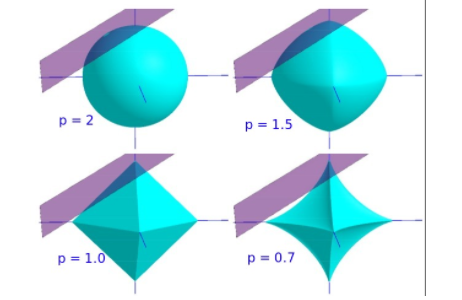
用紫色表示*面,用青色表示 norm 取同一个值的球形(等高线),问题如下:在*面 Ax = b *面内选出 norm 最小的最优解:
-
当 $1 \leq p$ 时,norm ball和*面的交点有多个。这是一个凸优化问题,可以用拉格朗日乘子来解决这个问题。
-
当 $0 < p < 1$ 时, norm ball 可行解十分稀疏,是一个非凸优化问题,解决这类问题很难,但是却有很好的稀疏性。
-
当 $p = 0$ 时, norm ball 上的点除了坐标轴,其他部分无限收缩,与*面的交点在某一个坐标轴上,非零系数只有一个。
回到之前讲的 MAP 模型, Sparse Modeling 模型就是非零系数限制在 $L$ 个之内(意味着解在至多 $L$ 个 atoms 组成的 span 里),尽可能接近**面:
回到图像去噪问题,图像的最大后验估计使我们想要的是什么?

还有一些问题有待解决:
-
这个优化问题怎么计算呢?
可以在满足 $|D\alpha - y|_2^2 \leq \epsilon^2$ 的情况下找最少非零元表示的 $\alpha$。
可以约束条件结合起来形成 $\lambda|\alpha|_0^0 + |D\alpha - y|^2_2$。
这三个是等效的。
-
另一个问题是得到的 $\alpha$ 唯一吗?我们选哪个 $\alpha$ ?
-
还有一个问题是,我们选选择哪个字典呢?

2. 总结: